시계열 확률 예측을 위한 분위수 회귀

원본 내용의 의미를 바꾸지 마시고, 내용을 미세 조정하고, 내용을 다시 작성하고, 계속해서 작성하지 마세요. "분위수 회귀는 이러한 요구를 충족하여 정량화된 확률로 예측 구간을 제공합니다. 이는 특히 응답 변수의 조건부 분포에 관심이 있는 경우 예측 변수와 응답 변수 간의 관계를 모델링하는 데 사용되는 통계 기술입니다. 기존 회귀와 달리 Quantile regression은 조건부 평균보다는 반응 변수의 조건부 크기를 추정하는 데 중점을 둡니다.”

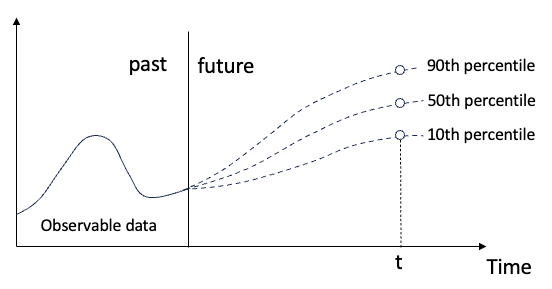그림 (A): Quantile regression

Quantile regression은 회귀 변수 X 집합과 설명된 변수 Y의 분위수 간의 선형 관계입니다.

기존 회귀모델은 실제로 설명변수와 설명변수의 관계를 연구하는 방법입니다. 그들은 설명 변수와 설명 변수 사이의 관계와 오류 분포에 중점을 둡니다. 중간 회귀와 분위수 회귀는 두 가지 일반적인 회귀 모델입니다. 이는 Koenker와 Bassett(1978)에 따라 처음 제안되었습니다.

보통 최소 제곱 회귀 추정기의 계산은 잔차 제곱합을 최소화하는 것을 기반으로 합니다. 분위수 회귀 추정량의 계산 역시 대칭 형태의 잔차 절대값을 최소화하는 것을 기반으로 합니다. 그 중 중앙값 회귀 연산은 최소 절대 편차 추정기(LAD, 최소 절대 편차 추정기)입니다.

분위수 회귀의 장점

설명변수의 조건부 분포에 대한 전체 그림을 설명합니다. 설명변수의 조건부 기대값(평균)을 분석할 뿐만 아니라 설명변수가 설명변수의 중앙값과 분위수에 어떤 영향을 미치는지 분석합니다. 변수 등을 설명했습니다. 서로 다른 분위수에서의 회귀 계수 추정치는 종종 다릅니다. 즉, 설명 변수는 서로 다른 분위수에 대해 서로 다른 효과를 갖습니다. 따라서 설명 변수의 서로 다른 분위수의 서로 다른 효과는 설명된 변수에 서로 다른 영향을 미칩니다.

최소 곱셈 방법과 비교하여 중앙값 회귀 추정 방법은 이상값에 더 강력하며 분위수 회귀는 오차 항에 대한 강력한 가정을 요구하지 않으므로 비정규 상태에 대한 분포, 중앙값 회귀 계수 양 더 건강해졌습니다. 동시에 분위수 회귀 시스템의 수량 추정은 더욱 강력해집니다.

몬테카를로 시뮬레이션에 비해 분위수 회귀의 장점은 무엇인가요? 첫째, 분위수 회귀는 예측 변수가 주어지면 반응 변수의 조건부 크기를 직접 추정합니다. 이는 몬테카를로 시뮬레이션과 같이 가능한 많은 결과를 생성하는 대신 응답 변수 분포의 특정 크기에 대한 추정치를 제공한다는 의미입니다. 이는 5분위수, 4분위수 또는 극한 크기와 같은 다양한 수준의 예측 불확실성을 이해하는 데 특히 유용합니다. 둘째, 분위수 회귀는 관측 데이터를 이용하여 변수 간의 관계를 추정하고, 이 관계를 기반으로 예측하는 모델 기반 예측 불확실성 추정 방법을 제공합니다. 대조적으로 몬테카를로 시뮬레이션은 입력 변수에 대한 확률 분포를 지정하고 무작위 샘플링을 기반으로 결과를 생성하는 데 의존합니다.

NeuralProphet은 (1) 분위수 회귀 및 (2) 등각 분위수 회귀라는 두 가지 통계 기법을 제공합니다. 등각 분위수 예측 기술은 분위수 회귀를 수행하기 위한 교정 프로세스를 추가합니다. 이 기사에서는 Neural Prophet의 분위수 회귀 모듈을 사용하여 분위수 회귀 예측을 수행합니다. 이 모듈은 예측 결과가 관찰된 데이터의 분포와 일치하는지 확인하기 위해 보정 프로세스를 추가합니다. 이 장에서는 Neural Prophet의 분위수 회귀 모듈을 사용합니다.

환경 요구사항

NeuralProphet을 설치하세요.

!pip install neuralprophet!pip uninstall numpy!pip install git+https://github.com/ourownstory/neural_prophet.git numpy==1.23.5

필요한 라이브러리를 가져옵니다.

%matplotlib inlinefrom matplotlib import pyplot as pltimport pandas as pdimport numpy as npimport loggingimport warningslogging.getLogger('prophet').setLevel(logging.ERROR)warnings.filterwarnings("ignore")

Dataset

공유 자전거 데이터. 데이터 세트는 일일 임대 수요는 물론 온도나 풍속과 같은 기타 기상 필드를 포함하는 다변량 데이터 세트입니다.

data = pd.read_csv('/bike_sharing_daily.csv')data.tail()

사진 (B) : 공유자전거공유자전거의 수를 표시해 보세요. 우리는 두 번째 해에 수요가 증가하고 계절적 패턴을 따르는 것을 관찰했습니다.

# convert string to datetime64data["ds"] = pd.to_datetime(data["dteday"])# create line plot of sales dataplt.plot(data['ds'], data["cnt"])plt.xlabel("date")plt.ylabel("Count")plt.show()

그림 (C) : 일일 자전거 대여 수요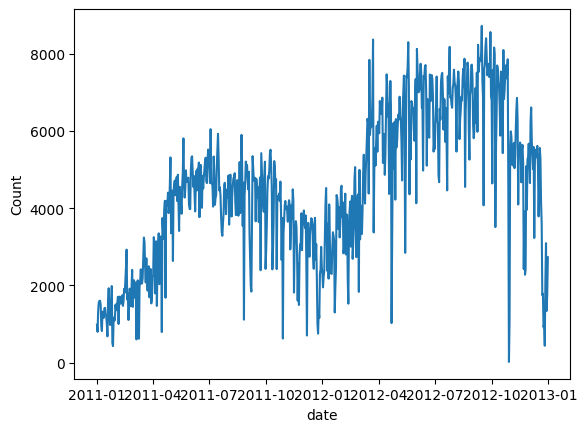 모델링을 위한 가장 기본적인 데이터를 준비합니다. NeuralProphet에는 Prophet과 동일한 열 이름 ds 및 y가 필요합니다.

rreee

构建分位数回归模型

直接在 NeuralProphet 中构建分位数回归。假设我们需要第 5、10、50、90 和 95 个量级的值。我们指定 quantile_list = [0.05,0.1,0.5,0.9,0.95]，并打开参数 quantiles = quantile_list。

from neuralprophet import NeuralProphet, set_log_levelquantile_list=[0.05,0.1,0.5,0.9,0.95 ]# Model and predictionm = NeuralProphet(quantiles=quantile_list,yearly_seasnotallow=True,weekly_seasnotallow=True,daily_seasnotallow=False)m = m.add_country_holidays("US")m.set_plotting_backend("matplotlib")# Use matplotlibdf_train, df_test = m.split_df(df, valid_p=0.2)metrics = m.fit(df_train, validation_df=df_test, progress="bar")metrics.tail()

分位数回归预测

我们将使用 .make_future_dataframe()为预测创建新数据帧，NeuralProphet 是基于 Prophet 的。参数 n_historic_predictions 为 100，只包含过去的 100 个数据点。如果设置为 True，则包括整个历史数据。我们设置 period=50 来预测未来 50 个数据点。

future = m.make_future_dataframe(df, periods=50, n_historic_predictinotallow=100) #, n_historic_predictinotallow=1)# Perform prediction with the trained modelsforecast = m.predict(df=future)forecast.tail(60)

预测结果存储在数据框架 predict 中。

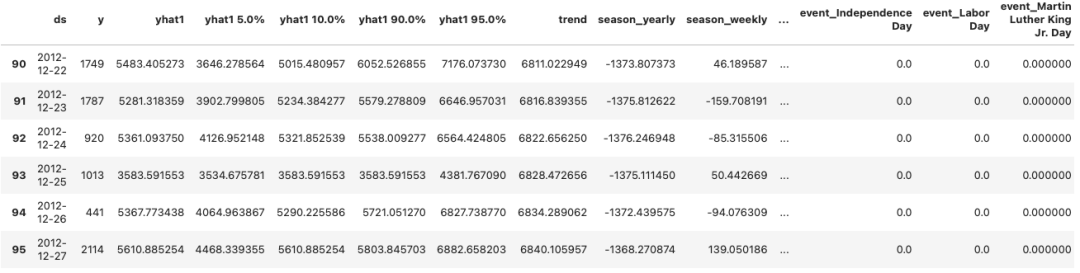图 (D)：预测

上述数据框架包含了绘制地图所需的所有数据元素。

m.plot(forecast, plotting_backend="plotly-static"#plotting_backend = "matplotlib")

预测区间是由分位数值提供的！

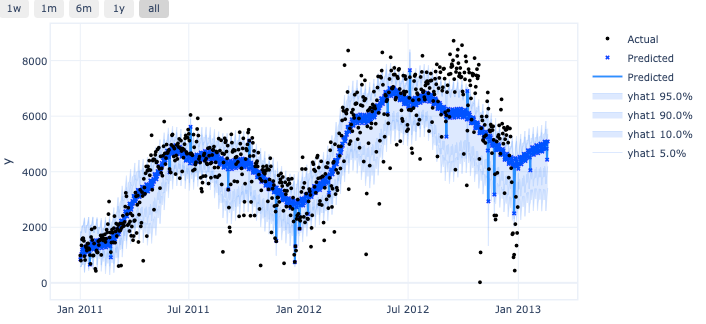图 (E)：分位数预测

预测区间和置信区间的区别

预测区间和置信区间在流行趋势中很有帮助，因为它们可以量化不确定性。它们的目标、计算方法和应用是不同的。下面我将用回归来解释两者的区别。在图(F)中，我在左边画出了线性回归，在右边画出了分位数回归。

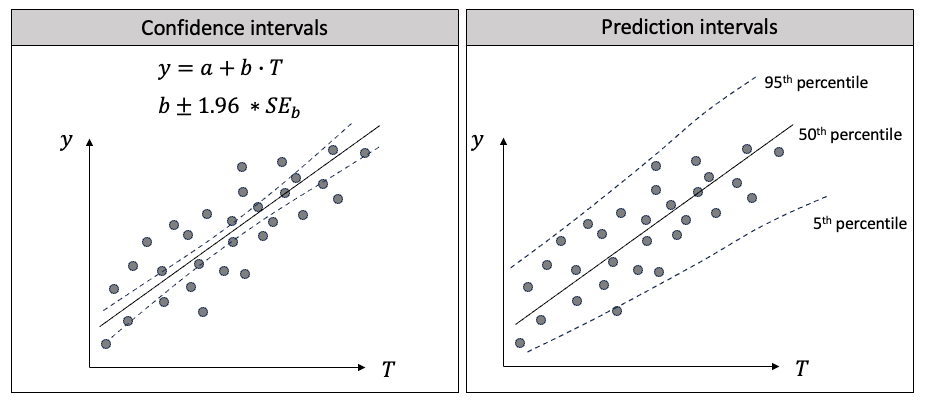图(F)：置信区间与预测区间的区别

首先，它们的目标不同：

• 线性回归的主要目标是找到一条线，使预测值尽可能接近给定自变量值时因变量的条件均值。
• 分位数回归旨在提供未来观测值的范围，在一定的置信度下。它估计自变量与因变量条件分布的不同量化值之间的关系。

其次，它们的计算方法不同：

• 在线性回归中，置信区间是对自变量系数的区间估计，通常使用普通最小二乘法 (OLS) 找出数据点到直线的最小总距离。系数的变化会影响预测的条件均值 Y。
• 在分位数回归中，你可以选择依赖变量的不同量级来估计回归系数，通常是最小化绝对偏差的加权和，而不是使用OLS方法。

第三，它们的应用不同：

• 在线性回归中，预测的条件均值有 95% 的置信区间。置信区间较窄，因为它是条件平均值，而不是整个范围。
• 在分位数回归中，预测值有 95% 的概率落在预测区间的范围内。

写在最后

本文介绍了分位数回归预测区间的概念，以及如何利用 NeuralProphet 生成预测区间。我们还强调了预测区间和置信区间之间的差异，这在商业应用中经常引起混淆。后面将继续探讨另一项重要的技术，即复合分位数回归（CQR），用于预测不确定性。

위 내용은 시계열 확률 예측을 위한 분위수 회귀의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!