为什么说浮点数缺乏精确性? python中浮点数运算问题
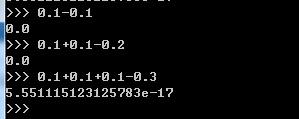 python中如图的运算为什么结果接近零而不为零 是什么原因造成的? 浮点数缺乏精确性应该怎么解释? 为什么前两个运算式没出现问题 最后一个出现了问题? 请教
python中如图的运算为什么结果接近零而不为零 是什么原因造成的? 浮点数缺乏精确性应该怎么解释? 为什么前两个运算式没出现问题 最后一个出现了问题? 请教回复内容:
这是因为小数以二进制形式表示时的有穷性导致的。(下面的说法,不完全准确,只是帮助理解)以下是之前我在另一个地方对一个类似问题的解答,因为内容差不多,就直接搬过来了(本人略懒,希望有所帮助):
#################################此处开始####################################
我们知道,将一个小数转化为二进制表示的方式是,不断的乘2,取其中的整数部分。例如:
+----------------------------------------------------------------------------------------------------------------------------------+
(1) 0.625*2 = 1.25, 整数部分为1,小数部分为0.25
(2) 0.25 * 2 = 0.5 , 整数部分为0,小数部分为0.5
(3) 0.5 * 2 = 1 , 整数部分为1,小数部分为0
+----------------------------------------------------------------------------------------------------------------------------------+
所以0.625的二进制表示就是0.101。
然而有些小数,例如0.4,并不能够精确的转化为二进制表示,用上面的这种方法计算:
+----------------------------------------------------------------------------------------------------------------------------------+
(1) 0.4*2=0.8 整数部分为0,小数部分为0.8
(2) 0.8*2=1.6 整数部分为1,小数部分为0.6
(3) 0.6*2=1.2 整数部分为1,小数部分为0.2
(4) 0.2*2=0.4 整数部分为0,小数部分为0.4
(5) 0.4*2=0.8 整数部分为0,小数部分为0.8
(6) 0.8*2=1.6 整数部分为1,小数部分为0.6
(7) 0.6*2=1.2 整数部分为1,小数部分为0.2
……
+----------------------------------------------------------------------------------------------------------------------------------+
所以0.4转化为二进制,应该是0.0110... 这样一个无限循环小数。
计算机的内存、cpu寄存器等等这些硬件单元都是有限的,只能表示有限位数的二进制位,因此存储的二进制小数就会和实际转换而成的二进制数有一定的误差。(你可以试着将0.3转化为二进制表示,也将出现一个循环小数。)
实际上,大多数情况下,小数在计算机中是以一种类似科学计数法的形式表示的,具体的可以参考一下其他的资料。但即便如此,仍然存在误差。
所以在python中不建议直接将两个浮点数进行大小比较,或者做精确的计算,往往会得到意想不到的结果。当然,如果非要用,可以参考decimal模块的相关内容。 请将十进制数字0.1转换成二进制浮点数。 这不是Python的问题,而是实数的无限精度跟计算机的有限内存之间的矛盾。
举个例子,假如说我只能使用整数(即只精确到个位,计算机内的浮点数也只有有限精度,以C语言中的双精度浮点数double为例,精度为52个二进制位),要表示任意实数(无限精度)的时候我就只能通过舍入(rounding)来近似表示。
比如1.2我会表示成1,2.4表示成2,3.6表示成4.
所以呢?
在算1.2 - 1.2的时候,由于计算机表示的问题,我算的实际上是1 - 1,结果是0,碰巧蒙对了;
在算1.2 + 1.2 - 2.4的时候,由于计算机表示的问题,我算的实际上是1 + 1 - 2,结果是0,再次蒙对了;
但是在算1.2 + 1.2 + 1.2 - 3.6的时候,由于计算机表示的问题,我算的实际上是1 + 1 + 1 - 4,结果是-1,运气没那么好啦!
这里的1.2, 2.4, 3.6就相当于你问题里的0.1, 0.2和0.3,1, 2, 4则是真正在计算机内部进行运算的数值,我说清楚了吗?
其他请看IEEE 754浮点数标准,比如CSAPP第二章啥的(虽然估计你没兴趣看)。
另:不仅仅是浮点数的在计算机内部的表示有误差,运算本身也可能会有误差。比如整数2可以在计算机内准确表示,但是要算根号2就有误差了;再比如两个浮点数相除,本来两个数都是精确表示的,但除的结果精度却超出了计算机内实数的表示范围,然后就有误差了。 计算机智能处理可数集合的运算,但是全体实数是不可数的,所以计算机只能用一些奇怪的方法来拟合他,于是就产生了浮点数。 这个不是python 的问题,所有基于二进制的浮点数都会有这个问题,原因在于大部分浮点数转换为二进制后都是无限循环小数,而浮点数不可能用无限大的内存来储存,所以会有舍入的误差
详细可以看代码之谜(五) 来个 @vczh 答案的通俗版,比如用 10 个箱子装100个球,规定每个箱子只能装一个球,那显然是装不下所有球的。类似,double类型是 64bit 的,最多能表达 2^64 个数,实数有多少呢?无数个,所以 double 类型是装不下所有实数的,只能表达一个近似值。 9.4. decimal 计算机所有信息的存储使用二进制表示,像 @vczh 所说,有限的「位」,无法表示无数个数,那么,小数用二进制表示法,只能表示那些能被写成
 的数。
的数。0.1 的二进制表示为 0.000110011[0011]...,因为是无限循环的,无法用有限的位表示,所以计算机系统会进行舍入,以求用最接近的值来表示,这里涉及到不同的舍入方式,具体请见深入理解计算机系统,本答案也是参考该书。 大白话版的很多人都说了,就是计算机有限的数字表示不了数学中无穷的数。
楼主如果有一定计算机或者数学基础可以搜一下IEEE754,电脑是如何表示浮点数的一种协议。看懂了那个协议就知道为什么了~
如果看不懂IEEE754那就需要研究下数学中各种进制~主要是二进制、十进制和他们的关系。 自傲的人类!有本事你直接喂它2进制数,看看还有没有这种精度问题。

핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

AI Hentai Generator
AI Hentai를 무료로 생성하십시오.

인기 기사

뜨거운 도구

메모장++7.3.1
사용하기 쉬운 무료 코드 편집기

SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.

스튜디오 13.0.1 보내기
강력한 PHP 통합 개발 환경

드림위버 CS6
시각적 웹 개발 도구

SublimeText3 Mac 버전
신 수준의 코드 편집 소프트웨어(SublimeText3)

뜨거운 주제
 7395
7395
 15
15
 1630
1630
 14
14
 1358
1358
 52
52
 1268
1268
 25
25
 1217
1217
 29
29
 휴대폰에서 XML을 PDF로 변환 할 때 변환 속도가 빠르나요?
Apr 02, 2025 pm 10:09 PM
휴대폰에서 XML을 PDF로 변환 할 때 변환 속도가 빠르나요?
Apr 02, 2025 pm 10:09 PM
모바일 XML에서 PDF의 속도는 다음 요인에 따라 다릅니다. XML 구조의 복잡성. 모바일 하드웨어 구성 변환 방법 (라이브러리, 알고리즘) 코드 품질 최적화 방법 (효율적인 라이브러리 선택, 알고리즘 최적화, 캐시 데이터 및 다중 스레딩 사용). 전반적으로 절대적인 답변은 없으며 특정 상황에 따라 최적화해야합니다.
 휴대 전화에서 XML 파일을 PDF로 변환하는 방법은 무엇입니까?
Apr 02, 2025 pm 10:12 PM
휴대 전화에서 XML 파일을 PDF로 변환하는 방법은 무엇입니까?
Apr 02, 2025 pm 10:12 PM
단일 애플리케이션으로 휴대 전화에서 직접 XML에서 PDF 변환을 완료하는 것은 불가능합니다. 두 단계를 통해 달성 할 수있는 클라우드 서비스를 사용해야합니다. 1. 클라우드에서 XML을 PDF로 변환하십시오. 2. 휴대 전화에서 변환 된 PDF 파일에 액세스하거나 다운로드하십시오.
 C 언어 합계의 기능은 무엇입니까?
Apr 03, 2025 pm 02:21 PM
C 언어 합계의 기능은 무엇입니까?
Apr 03, 2025 pm 02:21 PM
C 언어에는 내장 합계 기능이 없으므로 직접 작성해야합니다. 합계는 배열 및 축적 요소를 가로 질러 달성 할 수 있습니다. 루프 버전 : 루프 및 배열 길이를 사용하여 계산됩니다. 포인터 버전 : 포인터를 사용하여 배열 요소를 가리키며 효율적인 합계는 자체 증가 포인터를 통해 달성됩니다. 동적으로 배열 버전을 할당 : 배열을 동적으로 할당하고 메모리를 직접 관리하여 메모리 누출을 방지하기 위해 할당 된 메모리가 해제되도록합니다.
 XML을 PDF로 변환 할 수있는 모바일 앱이 있습니까?
Apr 02, 2025 pm 08:54 PM
XML을 PDF로 변환 할 수있는 모바일 앱이 있습니까?
Apr 02, 2025 pm 08:54 PM
XML을 PDF로 직접 변환하는 응용 프로그램은 근본적으로 다른 두 형식이므로 찾을 수 없습니다. XML은 데이터를 저장하는 데 사용되는 반면 PDF는 문서를 표시하는 데 사용됩니다. 변환을 완료하려면 Python 및 ReportLab과 같은 프로그래밍 언어 및 라이브러리를 사용하여 XML 데이터를 구문 분석하고 PDF 문서를 생성 할 수 있습니다.
 XML을 그림으로 변환하는 방법
Apr 03, 2025 am 07:39 AM
XML을 그림으로 변환하는 방법
Apr 03, 2025 am 07:39 AM
XSLT 변환기 또는 이미지 라이브러리를 사용하여 XML을 이미지로 변환 할 수 있습니다. XSLT 변환기 : XSLT 프로세서 및 스타일 시트를 사용하여 XML을 이미지로 변환합니다. 이미지 라이브러리 : Pil 또는 Imagemagick와 같은 라이브러리를 사용하여 XML 데이터에서 이미지를 그리기 및 텍스트 그리기와 같은 이미지를 만듭니다.
 권장 XML 서식 도구
Apr 02, 2025 pm 09:03 PM
권장 XML 서식 도구
Apr 02, 2025 pm 09:03 PM
XML 서식 도구는 규칙에 따라 코드를 입력하여 가독성과 이해를 향상시킬 수 있습니다. 도구를 선택할 때는 사용자 정의 기능, 특수 상황 처리, 성능 및 사용 편의성에주의하십시오. 일반적으로 사용되는 도구 유형에는 온라인 도구, IDE 플러그인 및 명령 줄 도구가 포함됩니다.
 XML을 PDF로 변환 할 수있는 모바일 앱이 있습니까?
Apr 02, 2025 pm 09:45 PM
XML을 PDF로 변환 할 수있는 모바일 앱이 있습니까?
Apr 02, 2025 pm 09:45 PM
XML 구조가 유연하고 다양하기 때문에 모든 XML 파일을 PDF로 변환 할 수있는 앱은 없습니다. XML에서 PDF의 핵심은 데이터 구조를 페이지 레이아웃으로 변환하는 것입니다. XML을 구문 분석하고 PDF를 생성해야합니다. 일반적인 방법으로는 요소 트리와 같은 파이썬 라이브러리를 사용한 XML 및 ReportLab 라이브러리를 사용하여 PDF를 생성하는 XML을 구문 분석합니다. 복잡한 XML의 경우 XSLT 변환 구조를 사용해야 할 수도 있습니다. 성능을 최적화 할 때는 멀티 스레드 또는 멀티 프로세스 사용을 고려하고 적절한 라이브러리를 선택하십시오.
 XML을 이미지로 변환하는 프로세스는 무엇입니까?
Apr 02, 2025 pm 08:24 PM
XML을 이미지로 변환하는 프로세스는 무엇입니까?
Apr 02, 2025 pm 08:24 PM
XML 이미지를 먼저 변환하려면 먼저 XML 데이터 구조를 결정한 다음 Python의 Matplotlib와 같은 적절한 그래픽 라이브러리를 선택하고 데이터 구조를 기반으로 시각화 전략을 선택하고 데이터 볼륨 및 이미지 형식을 고려하고 효율적인 라이브러리를 수행하거나 필요에 따라 PNG, JPEG 또는 SVG로 저장하십시오.




