C++의 부호 없는 유형 및 부호 있는 유형 관련 문제

Question

질문 1:
"표현 범위를 초과하는 부호 없는 유형에 값을 할당하면 결과는 부호 없는 유형이 나타내는 총 값 수에 모듈로 초기 값의 나머지가 됩니다."라는 문장을 어떻게 이해합니까? ? 예를 들어, 8비트 부호 없는 문자에 -1을 할당한 결과가 255인 이유는 무엇입니까?
제가 이해한 바는 다음과 같습니다. -1=11111111(첫 번째 1은 음수를 나타냄)인 경우 부호 없는 것으로 표현되면 11111111=255입니다.
그렇다면 부호 있는 유형에 표현 범위를 초과하는 값을 할당하는 이유는 무엇입니까?
질문 2
산술식에 부호 있는 유형과 부호 없는 유형이 모두 나타날 때 부호 있는 유형의 값이 양수인 경우, 부호 없는 유형으로 변환한 후의 값은 변환 전과 같은가요? 예를 들어 int a=1, unsigned b=1인 경우 a+b를 출력할 때 a는 먼저 unsigned로 변환됩니다. 변환 후 a는 1과 같을까요? int a=-1, unsingned b=2인 경우 a+b를 출력할 때 a는 먼저 unsigned 유형으로 변환됩니다. 변환 후 a의 값은 무엇입니까?
질문 2: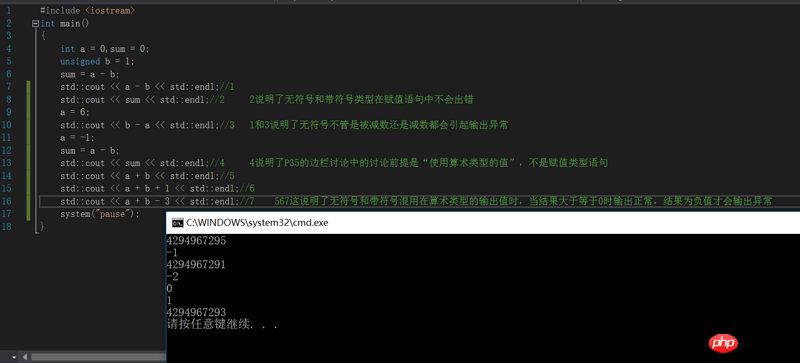

사진 속 네 번째 롱댓글처럼요.
책에서 말하는 것은 a+b의 결과가 무엇이든 a와 b 중 하나가 부호가 없고 다른 하나가 부호가 있는 한, 부호가 있는 것은 덧셈을 수행하기 전에 부호가 없는 것으로 변환되어야 한다는 것입니다. 실제로 그림 속 프로그램을 실행해 보니 a+b의 결과가 음수이고, a와 b 중 하나가 signed이고 다른 하나는 unsigned인 경우에만 결과가 unsigned로 변환된다는 생각이 들었습니다.
어느 것이 맞나요?

Answer 1

질문 1
사실 위의 설명은 기억의 관점에서 보면 매우 간단하다는 것을 알 수 있습니다. 부호 없는 것과 부호 있는 것의 차이는 기억의 저장이 아니라 기억의 획득이다. 예를 들어, -1을 8비트에 할당하는 예에서 부호가 없는 경우 마지막 8개의 이진 비트만 채워지고 나머지는 삭제됩니다. 이 8비트는 부호가 없기 때문에 그 안에 있는 모든 이진 비트는 숫자를 나타내므로 255입니다. 하지만 부호 있는 8비트인 경우 첫 번째 바이너리는 부호 비트를 나타내지만 할당 시 -1의 부호 비트는 8비트 데이터의 부호 비트가 되지 않으므로 8비트의 부호 비트는 데이터가 실제로 유효하지 않으므로 이 할당은 문제가 발생했습니다. 이 문장은 (-1)%256=255를 의미합니다. 여기서 256은 부호 없는 8비트(또는 범위)의 총 개수입니다.
질문 2
사실 위에서 언급한 것처럼 서명된 것과 서명되지 않은 것의 저장 방법은 동일하지만 읽는 방법이 다릅니다. 부호 있는 비트는 첫 번째 비트를 부호 비트로 처리하고 부호 없는 비트는 첫 번째 비트를 숫자 비트로 처리합니다. 귀하의 예에서 처음 a + b의 결과는 이진 표현에서 1 묶음입니다. 직접 출력하면 unsigned로 변환되기 때문에, 즉 unsigned 2개를 더하면 결과는 unsigned가 되고 unsigned인 1뭉치의 바이너리 출력은 4294967295가 되지만 a+b를 sum에 대입하면 sum 값을 저장합니다. 메모리에는 여전히 1이 많이 있지만 sum은 부호 있는 int이므로 읽을 때 첫 번째 비트가 부호 비트로 간주되므로 읽은 값은 -1입니다.
그러니까 질문 2에서는 연산 중 변환이 없다는 것이 아니라 값을 저장할 때 바이너리만 고려하고 부호가 있든 없든 차이가 없기 때문입니다. 부호 비트는 읽을 때만 판단되므로 출력 결과에 차이가 발생합니다.