二叉树的非递归后序遍历算法实例详解_javascript技巧
前序、中序、后序的非递归遍历中,要数后序最为麻烦,如果只在栈中保留指向结点的指针,那是不够的,必须有一些额外的信息存放在栈中。
方法有很多,这里只举一种,先定义栈结点的数据结构
typedef struct{Node * p; int rvisited;}SNode //Node 是二叉树的结点结构,rvisited==1代表p所指向的结点的右结点已被访问过。
lastOrderTraverse(BiTree bt){
//首先,从根节点开始,往左下方走,一直走到头,将路径上的每一个结点入栈。
p = bt;
while(bt){
push(bt, 0); //push到栈中两个信息,一是结点指针,一是其右结点是否被访问过
bt = bt.lchild;
}
//然后进入循环体
while(!Stack.empty()){ //只要栈非空
sn = Stack.getTop(); // sn是栈顶结点
//注意,任意一个结点N,只要他有左孩子,则在N入栈之后,N的左孩子必然也跟着入栈了(这个体现在算法的后半部分),所以当我们拿到栈顶元素的时候,可以确信这个元素要么没有左孩子,要么其左孩子已经被访问过,所以此时我们就不关心它的左孩子了,我们只关心其右孩子。
//若其右孩子已经被访问过,或是该元素没有右孩子,则由后序遍历的定义,此时可以visit这个结点了。
if(!sn.p.rchild || sn.rvisited){
p = pop();
visit(p);
}
else //若它的右孩子存在且rvisited为0,说明以前还没有动过它的右孩子,于是就去处理一下其右孩子。
{
//此时我们要从其右孩子结点开始一直往左下方走,直至走到尽头,将这条路径上的所有结点都入栈。
//当然,入栈之前要先将该结点的rvisited设成1,因为其右孩子的入栈意味着它的右孩子必将先于它被访问(这很好理解,因为我们总是从栈顶取出元素来进行visit)。由此可知,下一次该元素再处于栈顶时,其右孩子必然已被visit过了,所以此处可以将rvisited设置为1。
sn.rvisited = 1;
//往左下方走到尽头,将路径上所有元素入栈
p = sn.p.rchild;
while(p != 0){
push(p, 0);
p = p.lchild;
}
}//这一轮循环已结束,刚刚入栈的那些结点我们不必管它了,下一轮循环会将这些结点照顾的很好。
}
}

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

Video Face Swap
Tukar muka dalam mana-mana video dengan mudah menggunakan alat tukar muka AI percuma kami!

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1389
1389
 52
52
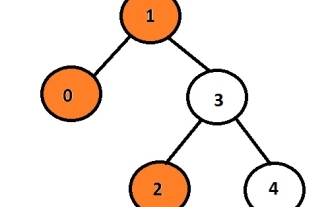 Cetak paparan kiri pokok binari dalam bahasa C
Sep 03, 2023 pm 01:25 PM
Cetak paparan kiri pokok binari dalam bahasa C
Sep 03, 2023 pm 01:25 PM
Tugasnya adalah untuk mencetak nod kiri pokok binari yang diberikan. Mula-mula, pengguna akan memasukkan data, dengan itu menjana pokok binari, dan kemudian mencetak pandangan kiri pokok yang terhasil. Setiap nod boleh mempunyai paling banyak 2 nod anak jadi atur cara ini mesti mengulangi hanya penunjuk kiri yang dikaitkan dengan nod jika penunjuk kiri tidak batal bermakna ia akan mempunyai beberapa data atau penunjuk yang dikaitkan dengannya jika tidak, ia akan dicetak dan dipaparkan sebagai anak kiri keluaran. ContohInput:10324Output:102Di sini, nod oren mewakili pandangan kiri pokok binari. Dalam graf yang diberikan, nod dengan data 1 adalah nod akar jadi ia akan dicetak dan bukannya pergi ke anak kiri ia akan mencetak 0 dan kemudian ia akan pergi ke 3 dan mencetak anak kirinya iaitu 2 . Kita boleh menggunakan kaedah rekursif untuk menyimpan tahap nod
 Penjelasan terperinci tentang struktur pokok binari di Jawa
Jun 16, 2023 am 08:58 AM
Penjelasan terperinci tentang struktur pokok binari di Jawa
Jun 16, 2023 am 08:58 AM
Pokok binari ialah struktur data biasa dalam sains komputer dan struktur data yang biasa digunakan dalam pengaturcaraan Java. Artikel ini akan memperkenalkan struktur pokok binari di Jawa secara terperinci. 1. Apakah pokok binari? Dalam sains komputer, pokok binari ialah struktur pokok di mana setiap nod mempunyai paling banyak dua nod anak. Antaranya, nod anak kiri lebih kecil daripada nod induk, dan nod anak kanan lebih besar daripada nod induk. Dalam pengaturcaraan Java, pokok binari biasanya digunakan untuk mewakili pengisihan, mencari dan meningkatkan kecekapan pertanyaan data. 2. Pelaksanaan pokok binari di Jawa Di Jawa, pokok binari
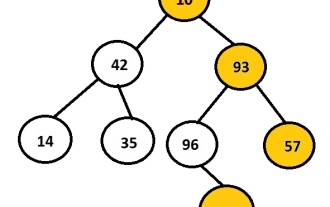 Dalam bahasa C, cetak pandangan kanan pokok binari
Sep 16, 2023 pm 11:13 PM
Dalam bahasa C, cetak pandangan kanan pokok binari
Sep 16, 2023 pm 11:13 PM
Tugasnya adalah untuk mencetak nod kanan pokok binari yang diberikan. Mula-mula pengguna akan memasukkan data untuk mencipta pokok binari dan kemudian mencetak pandangan kanan pokok yang terhasil. Imej di atas menunjukkan pepohon binari yang dicipta menggunakan nod 10, 42, 93, 14, 35, 96, 57 dan 88, dengan nod di sebelah kanan pepohon dipilih dan dipaparkan. Contohnya, 10, 93, 57, dan 88 ialah nod paling kanan bagi pokok binari. Contoh Input:1042931435965788Output:10935788 Setiap nod mempunyai dua penuding, penuding kiri dan penuding kanan. Menurut soalan ini, program hanya perlu melintasi nod yang betul. Oleh itu, anak kiri nod tidak perlu dipertimbangkan. Pandangan kanan menyimpan semua nod yang merupakan nod terakhir dalam hierarki mereka. Oleh itu, kita boleh
 Bagaimana untuk melaksanakan traversal pokok binari menggunakan Python
Jun 09, 2023 pm 09:12 PM
Bagaimana untuk melaksanakan traversal pokok binari menggunakan Python
Jun 09, 2023 pm 09:12 PM
Sebagai struktur data yang biasa digunakan, pokok binari sering digunakan untuk menyimpan data, mencari dan mengisih. Melintasi pokok binari adalah salah satu operasi yang sangat biasa. Sebagai bahasa pengaturcaraan yang mudah dan mudah digunakan, Python mempunyai banyak kaedah untuk melaksanakan traversal pokok binari. Artikel ini akan memperkenalkan cara menggunakan Python untuk melaksanakan traversal prapesanan, tertib dan pasca pesanan bagi pokok binari. Asas Pokok Binari Sebelum mempelajari cara melintasi pokok binari, kita perlu memahami konsep asas pokok binari. Pokok binari terdiri daripada nod, setiap nod mempunyai nilai dan dua nod anak (nod anak kiri dan nod anak kanan
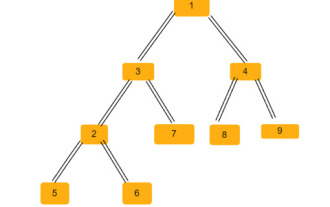 Bilangan segi tiga sama kaki dalam pokok binari
Sep 05, 2023 am 09:41 AM
Bilangan segi tiga sama kaki dalam pokok binari
Sep 05, 2023 am 09:41 AM
Pokok binari ialah struktur data di mana setiap nod boleh mempunyai sehingga dua nod anak. Kanak-kanak ini dipanggil anak kiri dan anak kanan masing-masing. Katakan kita diberi perwakilan tatasusunan induk, anda perlu menggunakannya untuk mencipta pokok binari. Pokok binari mungkin mempunyai beberapa segi tiga sama kaki. Kita perlu mencari jumlah bilangan segi tiga sama kaki yang mungkin dalam pokok binari ini. Dalam artikel ini, kami akan meneroka beberapa teknik untuk menyelesaikan masalah ini dalam C++. Memahami masalah memberi anda tatasusunan induk. Anda perlu mewakilinya dalam bentuk pokok binari supaya indeks tatasusunan membentuk nilai nod pokok dan nilai dalam tatasusunan memberikan nod induk indeks tertentu itu. Ambil perhatian bahawa -1 sentiasa menjadi induk akar. Diberikan di bawah adalah tatasusunan dan perwakilan pokok binarinya. Parentarray=[0,-1,3,1,
 Penjelasan terperinci tentang pelaksanaan pokok binari Java dan kes aplikasi tertentu
Jun 15, 2023 pm 11:03 PM
Penjelasan terperinci tentang pelaksanaan pokok binari Java dan kes aplikasi tertentu
Jun 15, 2023 pm 11:03 PM
Penjelasan terperinci tentang pelaksanaan pepohon binari Java dan kes aplikasi tertentu Pepohon binari ialah struktur data yang sering digunakan dalam sains komputer dan boleh melakukan operasi carian dan isihan yang sangat cekap. Dalam artikel ini, kita akan membincangkan cara untuk melaksanakan pokok binari di Jawa dan beberapa kes aplikasi khususnya. Definisi Pokok Binari Pokok binari ialah struktur data yang sangat penting, terdiri daripada nod akar (nod atas pokok) dan beberapa subpokok kiri dan subpokok kanan. Setiap nod mempunyai paling banyak dua nod anak, nod anak di sebelah kiri dipanggil subtree kiri, dan nod anak di sebelah kanan dipanggil subtree kanan. Jika nod tidak mempunyai
 Algoritma pokok binari dalam PHP dan Soalan Lazim
Jun 09, 2023 am 09:33 AM
Algoritma pokok binari dalam PHP dan Soalan Lazim
Jun 09, 2023 am 09:33 AM
Dengan pembangunan berterusan pembangunan web, PHP, sebagai bahasa skrip pelayan yang digunakan secara meluas, algoritma dan struktur datanya menjadi semakin penting. Di antara algoritma dan struktur data ini, algoritma pokok binari adalah konsep yang sangat penting. Artikel ini akan memperkenalkan algoritma pokok binari dan aplikasinya dalam PHP, serta jawapan kepada soalan biasa. Apakah pokok binari? Pokok binari ialah struktur pokok di mana setiap nod mempunyai paling banyak dua nod anak, nod anak kiri dan nod anak kanan. Jika nod tidak mempunyai nod anak, ia dipanggil nod daun. Pokok binari sering digunakan untuk mencari
 Kaedah dan aplikasi pelaksanaan pokok binari dalam PHP
Jun 18, 2023 pm 06:28 PM
Kaedah dan aplikasi pelaksanaan pokok binari dalam PHP
Jun 18, 2023 pm 06:28 PM
Dalam sains komputer, pokok binari ialah struktur data yang penting. Ia terdiri daripada nod dan tepi menghala kepada mereka, dengan setiap nod menyambung sehingga dua nod anak. Pokok binari digunakan secara meluas dalam bidang seperti algoritma carian, penyusun, pangkalan data dan pengurusan memori. Banyak bahasa pengaturcaraan menyokong pelaksanaan struktur data pokok binari, PHP menjadi salah satu daripadanya. Artikel ini akan memperkenalkan cara PHP melaksanakan pepohon binari dan aplikasinya. Definisi Pokok Binari Pepohon binari ialah struktur data yang terdiri daripada nod dan tepi yang menghala kepada mereka. Setiap nod disambungkan kepada paling banyak dua nod anak,




