 Peranti teknologi
Peranti teknologi
 AI
AI
 Gambaran keseluruhan perancangan laluan: berdasarkan pensampelan, carian dan pengoptimuman, semuanya selesai!
Gambaran keseluruhan perancangan laluan: berdasarkan pensampelan, carian dan pengoptimuman, semuanya selesai!
Gambaran keseluruhan perancangan laluan: berdasarkan pensampelan, carian dan pengoptimuman, semuanya selesai!
1 Gambaran keseluruhan kawalan keputusan dan perancangan gerakan
Kaedah kawalan keputusan semasa boleh dibahagikan kepada tiga kategori: perancangan berurutan, perancangan sedar tingkah laku dan perancangan hujung ke hujung.
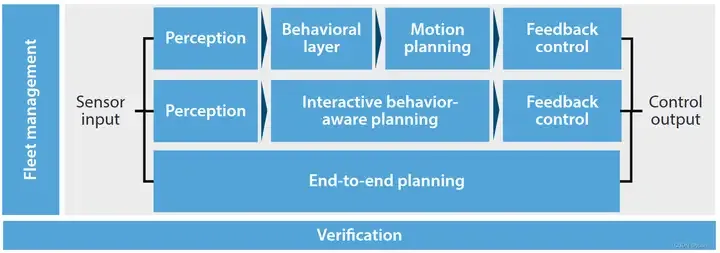
- perancangan berurutan: Kaedah yang paling tradisional, tiga bahagian persepsi, keputusan dan kawalan adalah agak jelas
- perancangan yang menyerlahkan tingkah laku yang pertama: Comparison aware; pengenalan kerjasama manusia-mesin Pemanduan, kerjasama kenderaan-jalan, dan anggaran risiko kenderaan kepada persekitaran dinamik luaran
- perancangan hujung ke hujung: teknologi DL dan DRL, dengan bantuan sejumlah besar latihan data, memperoleh; segala-galanya daripada maklumat deria seperti imej kepada input kawalan kenderaan seperti sudut stereng Perhubungan adalah salah satu kaedah yang paling popular pada masa kini.
Artikel ini akan memperkenalkan perancangan berurutan, menerangkan proses kawalan persepsi kenderaan autonomi mengikut keseluruhan urutan kawalan keputusan, dan akhirnya merumuskan secara ringkas masalah yang perlu diselesaikan yang dinyatakan di atas.
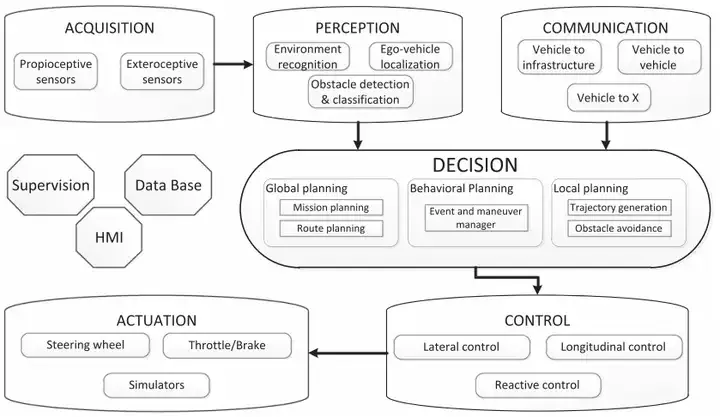
Kontrol Senibina untuk kenderaan automatik
2 Proses Perancangan Perancangan Pathsequential diringkaskan secara ringkas sebagai perancangan Path- & gt; diterangkan dalam artikel ini Perancangan tergolong dalam langkah pertama dan ketiga.
https://www.php.cn/link/aa7d66ed4b1c618962d406535c4d282a
Mengenai masalah penjanaan trajektori untuk kenderaan tanpa pemandu🜎 terdapat dua jenis kenderaan tanpa pemandu:kaedah penguraian halaju laluan 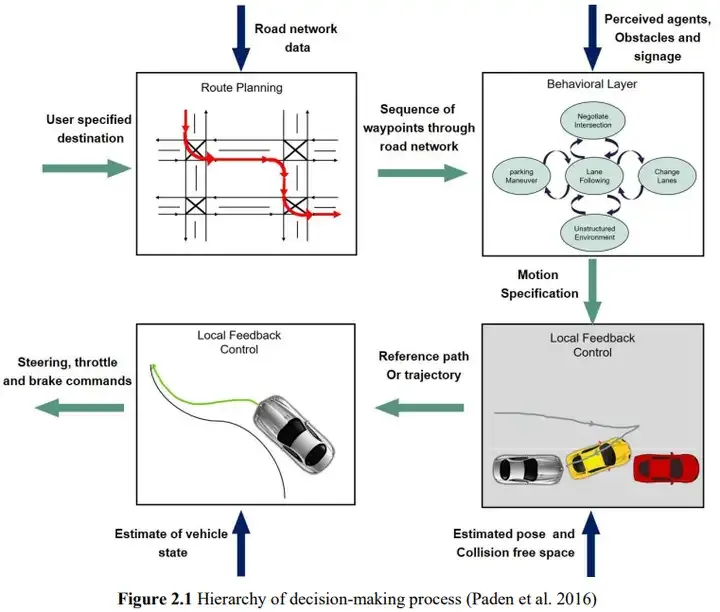 , berbanding yang pertama, kelajuan laluan adalah kurang sukar, jadi ia lebih biasa digunakan.
, berbanding yang pertama, kelajuan laluan adalah kurang sukar, jadi ia lebih biasa digunakan.
Perancangan laluan boleh dibahagikan kepada empat kategori utama: algoritma berdasarkan sampling diwakili oleh PRM dan RRT, algoritma berdasarkan carian diwakili oleh penjanaan A* dan D*, algoritma berdasarkan
interpolasipemasangan yang diwakili oleh lengkung β-spline, dan algoritma kawalan optimum untuk perancangan laluan tempatan yang diwakili oleh MPC. Bahagian ini akan diterangkan dalam susunan di atas:
Semakan Algoritma Teknologi Perancangan Pergerakan3.1.1 Algoritma asas PRM dan RRT
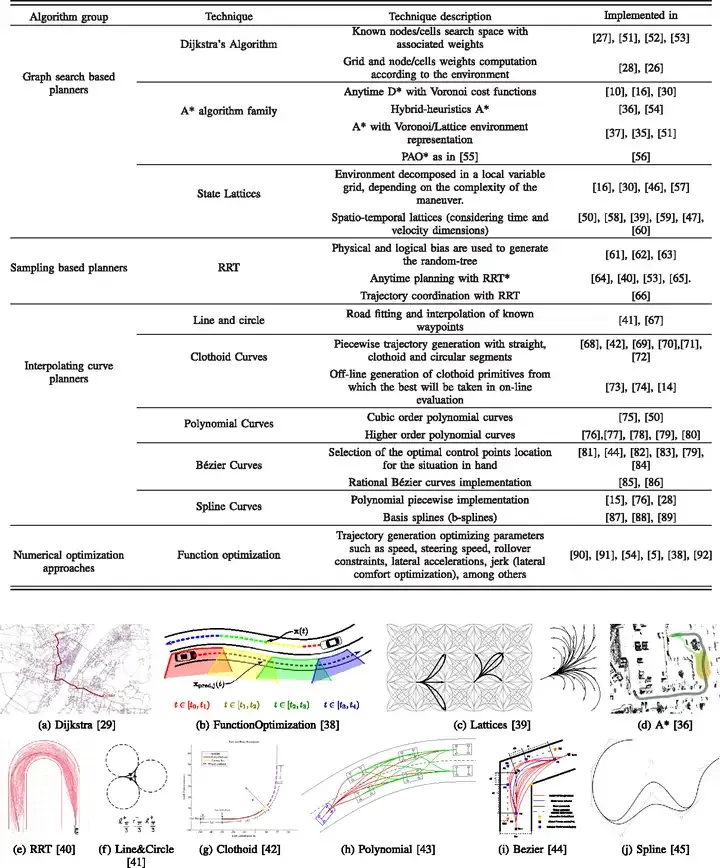
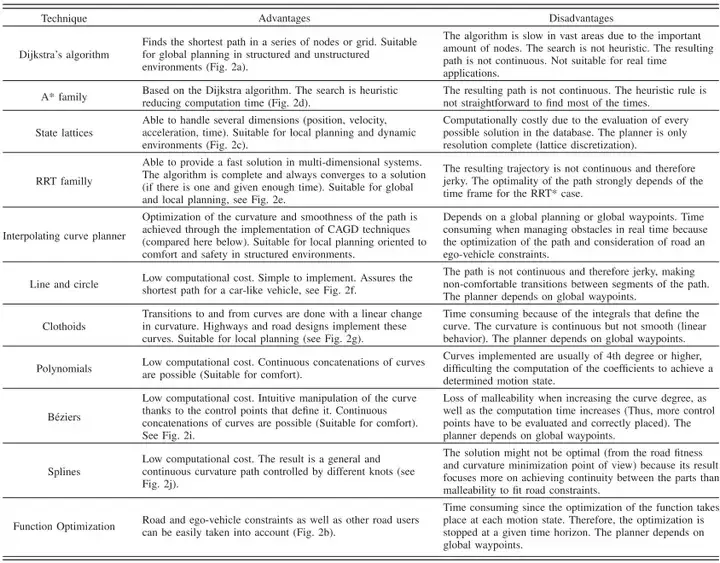
Algoritma PRM (Peta Jalan Kebarangkalian). PRM terutamanya terdiri daripada dua langkah, satu peringkat pembelajaran dan satu lagi peringkat pertanyaan.
Langkah pertama, peringkat pembelajaran: sampel n titik secara seragam dan rawak di kawasan selamat dalam ruang keadaan, dan padamkan titik di mana sampel jatuh pada halangan, kemudian sambungkan titik bersebelahan dan lakukan pengesanan perlanggaran, dan hapuskan bukan -perlanggaran -sambungan bebas, dan akhirnya mendapat graf bersambung.
Langkah kedua, peringkat pertanyaan: Untuk sepasang keadaan awal dan sasaran tertentu, gunakan nod pensampelan dan kesinambungan yang dibina dalam langkah sebelumnya dan gunakan kaedah carian graf (Dijkstra atau A*) untuk mencari laluan yang boleh dilaksanakan.Selepas menyiapkan pembinaan PRM, ia boleh digunakan untuk menyelesaikan masalah perancangan gerakan dalam keadaan awal dan sasaran yang berbeza, tetapi ciri ini tidak diperlukan untuk perancangan gerakan kenderaan tanpa pemandu. Di samping itu, PRM memerlukan sambungan yang tepat antara negeri, yang sangat sukar untuk masalah perancangan gerakan dengan kekangan pembezaan yang kompleks.
(2) RRT
RRT (Penerokaan Random Tree) dengan pantas. RRT sebenarnya mewakili satu siri algoritma berdasarkan idea pokok yang tumbuh secara rawak Ia kini merupakan algoritma yang paling banyak digunakan dengan varian pengoptimuman paling banyak dalam bidang robotik
① Permulaan pokok. set nod dan set tepi pokok , set nod hanya mengandungi keadaan awal, dan set tepi kosong② Pertumbuhan pokok: Sampel ruang keadaan secara rawak Apabila titik pensampelan jatuh di kawasan selamat ruang keadaan, pilih nod yang paling hampir dengan titik pensampelan dalam pokok semasa dan lanjutkan ke titik pensampelan trajektori tidak disambungkan dengan halangan Jika objek berlanggar, trajektori ditambah pada set tepi pokok, dan titik akhir trajektori ditambah pada set nod pokok
③ Ulang langkah ② sehingga ia berkembang kepada set keadaan sasaran Berbanding dengan graf tidak terarah PRM, RRT Apa yang dibina ialah struktur pokok dengan keadaan awal sebagai nod akar dan keadaan sasaran sebagai nod daun Untuk keadaan awal dan sasaran yang berbeza, pokok yang berbeza perlu dibina.
RRT tidak memerlukan sambungan yang tepat antara negeri dan lebih sesuai untuk menyelesaikan masalah dinamik pergerakan seperti perancangan pergerakan kenderaan tanpa pemandu.
3.1.2 Masalah dan penyelesaian kaedah pensampelan
Menyelesaikan kecekapan dan sama ada ia adalah penyelesaian yang optimum. Sebab mengapa PRM dan RRT mempunyai kebarangkalian kesempurnaan adalah kerana ia akan merentasi hampir semua kedudukan dalam ruang konfigurasi.
(1) Menyelesaikan kecekapan
Dari segi meningkatkan menyelesaikan kecekapan, idea teras mengoptimumkan RRT ialah membimbing pokok ke kawasan lapang iaitu cuba menjauhi halangan dan mengelakkan pemeriksaan berulang nod pada halangan Ini meningkatkan kecekapan. Penyelesaian utama:
① Persampelan seragam
Algoritma RRT piawai mensampel ruang keadaan secara seragam dan rawak Kebarangkalian nod dalam pokok semasa mendapat pengembangan adalah berkadar dengan kawasan nya. pokok itu akan bergerak ke arah negeri kawasan ruang kosong tumbuh, memenuhi kawasan bebas ruang negeri secara seragam. Algoritma
RRT-connect secara serentak membina dua pokok bermula dariawalkeadaan dan sasarannya masing-masing Apabila kedua-dua pokok tumbuh bersama, penyelesaian yang boleh dilaksanakan. Go-biaing memasukkan keadaan sasaran pada perkadaran tertentu ke dalam jujukan pensampelan rawak, membimbing pokok untuk berkembang ke arah keadaan sasaran, mempercepatkan penyelesaian dan meningkatkan kualiti penyelesaian.
heuristik RRT menggunakan fungsi heuristik untuk meningkatkan kebarangkalian pensampelan nod dengan kos pengembangan yang rendah dan mengira kos setiap nod dalam pepohon Walau bagaimanapun, dalam persekitaran yang kompleks, definisi fungsi kos adalah sukar untuk menyelesaikan masalah ini. f Kaedah pensampelan -bias mula-mula mendiskrisikan ruang keadaan menjadi grid, dan kemudian menggunakan algoritma Dijkstra untuk mengira kos pada setiap grid Nilai kos mata dalam kawasan grid adalah sama dengan nilai ini , dengan itu membina fungsi heuristik.② Metrik jarak yang dioptimumkan
Jarak digunakan untuk mengukur kos laluan antara dua konfigurasi, membantu dalam menjana fungsi kos heuristik dan membimbing arah pokok. Walau bagaimanapun, pengiraan jarak adalah sukar apabila halangan dipertimbangkan. Definisi jarak dalam perancangan gerakan menggunakan definisi yang serupa dengan jarak Euclidean. RG-RRT (RRT berpandukan rechability) boleh menghapuskan kesan jarak yang tidak tepat pada keupayaan penerokaan RRT Ia perlu mengira set nod yang boleh dicapai dalam pepohon Apabila jarak dari titik pensampelan ke nod adalah lebih besar daripada set boleh dicapai nod, jarak, nod boleh dipilih untuk pengembangan. . titik. resolusi lengkap RRT memperoleh kebarangkalian pengembangan denganmengurangkan nod dekat dengan halangan
Ia mendiskrisikan ruang input dan hanya menggunakannya sekali untuk input nod tertentu jika trajektori yang sepadan dengan input tertentu bertembung dengan halangan, maka A yang sepadan nilai penalti ditambah pada nod Semakin tinggi nilai penalti, semakin kecil kebarangkalian bahawa nod akan dikembangkan. RRT domain dinamik dan RRT domain dinamik adaptif mengehadkan kawasan pensampelan kepada ruang tempatan di mana pokok semasa terletak untuk mengelakkan nod yang hampir dengan halangan daripada kegagalan pengembangan berulang dan meningkatkan kecekapan algoritma.④ Tingkatkan prestasi masa nyata
Bila-bila masa RRT mula-mula membina RRT dengan cepat, memperoleh penyelesaian yang boleh dilaksanakan dan merekodkan kosnya, dan kemudian meneruskan pensampelan, tetapi hanya memasukkan nod yang bermanfaat untuk mengurangkan kos penyelesaian yang boleh dilaksanakan ke dalam pokok, dengan itu secara beransur-ansur memperoleh penyelesaian yang lebih baik. Perancangan semula menguraikan keseluruhan tugas perancangan kepada beberapa jujukan subtugasan masa yang sama, dan merancang tugas seterusnya semasa melaksanakan tugas semasa. (2) Terdapat terutamanya kaedah berikut untuk menyelesaikan masalah optimum
:Algoritma RGG (graf geometri rawak): PRM dengan sifat optimum asimptotik yang dipertingkatkan pada PRM standard dan RRT berdasarkan teori graf geometri rawak Algoritma RRG dan RRT
secara rawak mengambil n titik dalam ruang keadaan dan menyambungkan titik dengan jarak kurang daripada r(n) untuk membentuk RGG. RRT* Algoritma: Perkenalkan langkah "penyambungan semula" berdasarkan RRG untuk menyemak sama ada nod induk yang baru dimasukkan sebagai nod induk bagi titik bersebelahannya akan mengurangkan kos titik bersebelahan jika berlaku, alih keluar induk dan anak asal titik bersebelahan, mengambil titik sisipan semasa sebagai nod induknya, ini ialah algoritma RRT*.Algoritma LBT-RRT: Sebilangan besar sambungan nod dan pelarasan setempat menjadikan PRM dan RRT sangat tidak cekap. Algoritma LBT-RRT menggabungkan algoritma RRG dan RRT* untuk mendapatkan kecekapan yang lebih tinggi pada premis mendapatkan optimum tanpa gejala. . penyelesaian optimum
, algoritma kategori ini agak matang.
Asas algoritma berasaskan carian ialah kekisi keadaan ialah pendiskretan ruang keadaan Ia terdiri daripada nod keadaan dan primitif gerakan yang bermula dari nod dan mencapai nod bersebelahan. Nod keadaan boleh melepasi gerakan primitifnya bertukar kepada nod keadaan lain. Kekisi keadaan menukarkan ruang keadaan berterusan asal kepada graf carian Masalah perancangan gerakan menjadi mencari siri primitif gerakan yang mengubah keadaan awal kepada keadaan sasaran dalam graf Selepas membina kekisi keadaan, anda boleh menggunakan carian graf algoritma untuk mencari trajektori yang optimum. 3.2.1 Pembinaan algoritma asas Dijkstra dan A*Algoritma Dijkstra merentasi keseluruhan ruang konfigurasi, mencari jarak antara setiap dua grid, dan akhirnya memilih laluan terpendek dari titik permulaan ke titik sasaran, dengan keluasan priority Nature membawa kepada kecekapan yang sangat rendah Menambah fungsi heuristik pada algoritma ini, iaitu jarak dari nod yang dicari ke nod sasaran, dan mencari semula berdasarkan ini boleh mengelakkan ketidakcekapan yang disebabkan oleh carian global. Ini ialah A *Algoritma , seperti yang ditunjukkan dalam rajah di bawah, merah ialah kawasan carian.
Rajah 6: Perbandingan kesan algoritma A* dan Dijkstra 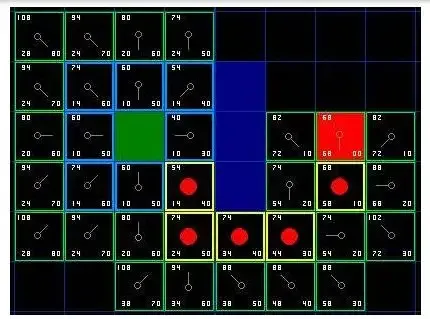
3.2.2 Masalah dan cadangan kaedah carian
Sama seperti algoritma berasaskan pensampelan juga perlu cekap dan algoritma ini. pengoptimuman seksual yang optimum.
Dari segi meningkatkan kecekapan, A* sendiri ialah algoritma perancangan statik Lanjutan daripada algoritma A* adalah berwajaran A*, yang seterusnya membimbing arah carian ke nod sasaran dengan meningkatkan berat fungsi heuristik kelajuan sangat pantas, tetapi Ia mudah untuk jatuh ke dalam minima tempatan dan tidak dapat menjamin penyelesaian optimum global. Untuk kenderaan bergerak, menggunakan algoritma terbitan A* D (dinamik A) boleh meningkatkan kecekapan. Juga berdasarkan pengaturcaraan dinamik ialah LPA Algoritma ini boleh mengendalikan keadaan di mana kos primitif gerakan grid keadaan berubah-ubah apabila persekitaran berubah, pelan optimum baharu boleh dirancang dengan mencari semula bilangan yang lebih kecil nod. Dibangunkan berdasarkan LPA , D*-Lite boleh mencapai hasil yang sama seperti D*, tetapi dengan kecekapan yang lebih tinggi.
, D*-Lite boleh mencapai hasil yang sama seperti D*, tetapi dengan kecekapan yang lebih tinggi.
Apabila mencari penyelesaian optimum, ARA* ialah algoritma carian bila-bila masa yang dibangunkan berdasarkan Weighted A* Ia memanggil algoritma Weighted A* beberapa kali dan mengurangkan berat fungsi heuristik dengan setiap panggilan boleh mencari penyelesaian yang boleh dilaksanakan dengan cepat Dengan memperkenalkan set INCONS, setiap kitaran boleh terus menggunakan maklumat kitaran sebelumnya untuk mengoptimumkan laluan dan secara beransur-ansur mendekati penyelesaian optimum.
Dari segi kecekapan dan pengoptimuman algoritma mengimbangi, Sandin aine et al mencadangkan algoritma MHA*, yang memperkenalkan pelbagai fungsi heuristik untuk memastikan bahawa salah satu fungsi heuristik dapat mencari penyelesaian optimum apabila digunakan secara bersendirian, dengan itu melalui penyelarasan Kos laluan. yang dihasilkan oleh fungsi heuristik yang berbeza boleh mengambil kira kecekapan dan keoptimuman algoritma. DMHA menjana fungsi heuristik yang sesuai dalam talian dan dalam masa nyata berdasarkan MHA, dengan itu mengelakkan masalah minimum setempat.
3.3 Algoritma berdasarkan padanan interpolasiAlgoritma berdasarkan pada interpolasi boleh ditakrifkan sebagai: berdasarkan siri set titik yang diketahui digunakan untuk menggambarkan peta jalan, dengan menggunakan interpolasi data dan
kaedah pemasangan lengkungmencipta laluan
yang akan dilalui oleh kereta pintar, yang boleh memberikankesinambungan
dan lebih tinggikebolehbezaan. Kaedah khusus adalah seperti berikut:
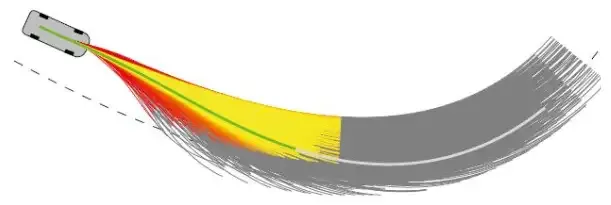
Keluk Dubai dan keluk Reeds and Sheep (RS) ialah laluan terpendek yang menghubungkan mana-mana dua titik dalam ruang konfigurasi, sepadan dengan situasi tanpa membalikkan dan dengan membalikkan masing-masing. Kesemuanya terdiri daripada lengkok kelengkungan maksimum dan garis lurus Terdapat ketakselanjaran kelengkungan pada sambungan antara lengkok dan garis lurus Apabila kenderaan sebenar bergerak pada selekoh sedemikian, ia mesti berhenti dan melaraskan stereng pada ketakselanjaran. kelengkungan untuk meneruskan pemanduan.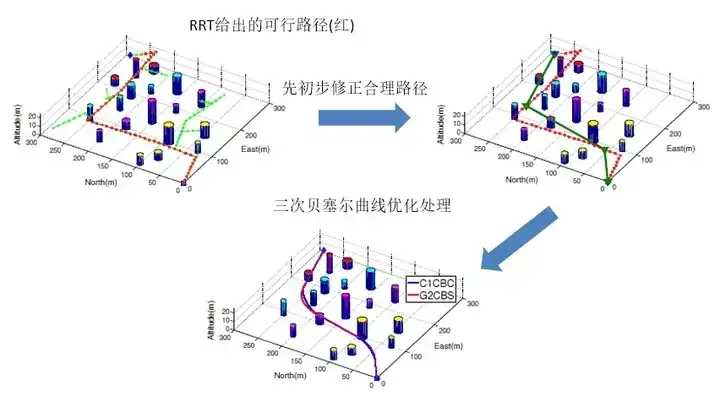
ialah kaedah yang paling biasa digunakan Ia boleh menetapkan pekali polinomial dengan memenuhi keperluan nod dan memperoleh kebolehbezaan berterusan yang lebih baik selalunya digunakan untuk kawalan kekangan membujur, dan polinomial tertib kelima selalunya. digunakan untuk kawalan kekangan membujur. Polinomial sering digunakan dalam kawalan kekangan sisi, dan polinomial tertib ketiga juga digunakan dalam memotong trajektori. Keluk spline mempunyai ekspresi tertutup dan boleh memastikan kesinambungan kelengkungan dengan mudah. Lengkung β-spline boleh mencapai kesinambungan kelengkungan, dan lengkung Bezier kubik boleh memastikan kesinambungan dan sempadan kelengkungan, dan jumlah pengiraan adalah agak kecil. Lengkung η^3 [43] ialah lengkung splin tujuh darjah, yang mempunyai sifat yang sangat baik: kesinambungan kelengkungan dan kesinambungan derivatif kelengkungan, yang sangat bermakna untuk kenderaan berkelajuan tinggi. Algoritma berdasarkan kawalan optimum diklasifikasikan ke dalam perancangan laluan, terutamanya kerana MPC boleh melakukan perancangan laluan tempatan untuk mengelakkan halangan Selain itu, MPC terutamanya Fungsinya adalah untuk menjejaki trajektori kepada kekangan dinamik dan kinematik yang diperlukan, isu yang dipertimbangkannya juga harus mempertimbangkan keselesaan, ketidakpastian maklumat deria, ketidakpastian komunikasi antara kenderaan pada masa hadapan, dan apabila merancang trajektori tempatan Pemandu juga boleh dimasukkan ke dalam gelung kawalan. Isu ketidakpastian yang disebutkan di atas dan memasukkan pemandu ke dalam gelung kawalan akan dibincangkan dalam Bahagian 4. Kajian MPC terutamanya bermula dari dua aspek: teori pengoptimuman dan amalan kejuruteraan. Untuk yang pertama, saya mengesyorkan Algoritma Pengoptimuman Convex oleh Dimitri P. Bertsekas dan Kawalan Ramalan Model: Teori, Pengiraan dan Reka Bentuk oleh James B. Rawlings. Dalam bidang bahasa Cina, buku pengoptimuman cikgu Liu Haoyang secara peribadi merasakan bahawa ia agak jelas dan mudah difahami. Untuk yang kedua, pertama sekali, buku MPC memandu sendiri Teacher Gong Jianwei amat disyorkan Terdapat masalah dengan demo dalam versi lama buku itu, tetapi semuanya telah diselesaikan dalam versi baharu. Terdapat banyak jenis model ramalan yang digunakan oleh MPC: seperti rangkaian neural konvolusi, kawalan kabur, ruang keadaan, dan lain-lain. Antaranya, yang paling biasa digunakan ialah kaedah ruang keadaan. MPC boleh dinyatakan secara ringkas sebagai: apabila kekangan dinamik, kinematik, dll. yang diperlukan dipenuhi, penyelesaian optimum model diselesaikan melalui cara berangka Penyelesaian optimum ialah pembolehubah kawalan persamaan keadaan, seperti sudut stereng , dsb., dan Gunakan kuantiti kawalan pada model kereta untuk mendapatkan kuantiti keadaan yang diperlukan, seperti kelajuan, pecutan, koordinat, dsb. Dapat dilihat dari huraian di atas bahawa kunci kepada MPC terletak pada penubuhan dan penyelesaian model Cara untuk memudahkan penubuhan model dan meningkatkan kecekapan penyelesaian adalah keutamaan. Kenderaan akan mengambil trajektori yang berbeza di bawah input kawalan yang berbeza, dan setiap trajektori sepadan dengan nilai fungsi objektif Kenderaan tanpa pemandu akan menggunakan algoritma penyelesaian untuk mencari kuantiti kawalan yang sepadan dengan nilai fungsi objektif minimum, dan menggunakannya pada kenderaan di atas , seperti yang ditunjukkan dalam rajah di bawah: Untuk mengurangkan kesukaran pemodelan, model medan tenaga potensi buatan juga digunakan untuk pemodelan Idea asas medan tenaga berpotensi buatan adalah serupa dengan medan elektrik, dan halangan di jalan raya adalah serupa dengan sumber medan dalam medan elektrik Caj dengan kekutuban cas yang berbeza. Tenaga potensi pada halangan (dinamik, statik) adalah lebih tinggi, dan kenderaan tanpa pemandu akan bergerak ke arah kedudukan tenaga berpotensi rendah. Syorkan projek sumber terbuka CppRobotics: dan perancangan secara manual contoh: 5.1 Kejuruteraan . Mengenai algoritma dalam bidang perancangan laluan, pada masa ini tiada tutorial yang komprehensif, tetapi perancangan gerakan NMPC Gong Jianwei boleh menjadi rujukan. 5.2 Teori Teori Pengoptimuman Artikel ini memperkenalkan garis besar perancangan laluan semasa dan memahami kaedah perancangan laluan semasa. Kandungannya sangat rumit, dan sukar untuk mempelajari semuanya dalam tempoh yang singkat tanpa orientasi aplikasi praktikal Anda hanya boleh menumpukan pada pembelajaran apabila diperlukan. 3.4 Algoritma berdasarkan kawalan optimum
4 Projek Sumber Terbuka
Konteks pembelajaran untuk bermula dalam bidang baharu ialah: Kejuruteraan,
Teori merujuk kepada memahami kandungan setiap algoritma perancangan laluan, sambil memahami kandungan setiap algoritma daripada keluasan, dan pada masa yang sama mempelajari butiran setiap algoritma dari
kedalaman merujuk kepada pemahaman prinsip matematik yang menyokong operasi algoritma ini dan sebab mengapa algoritma ini dijana (perspektif matematik).
Membina fungsi objektif dan kekangan dan mencari nilai ekstrem pada masa yang sama untuk mendapatkan pembolehubah kawalan optimum (laluan), yang tergolong dalam
6 Ringkasan
Atas ialah kandungan terperinci Gambaran keseluruhan perancangan laluan: berdasarkan pensampelan, carian dan pengoptimuman, semuanya selesai!. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1378
1378
 52
52
 Mengapakah Gaussian Splatting begitu popular dalam pemanduan autonomi sehingga NeRF mula ditinggalkan?
Jan 17, 2024 pm 02:57 PM
Mengapakah Gaussian Splatting begitu popular dalam pemanduan autonomi sehingga NeRF mula ditinggalkan?
Jan 17, 2024 pm 02:57 PM
Ditulis di atas & pemahaman peribadi pengarang Gaussiansplatting tiga dimensi (3DGS) ialah teknologi transformatif yang telah muncul dalam bidang medan sinaran eksplisit dan grafik komputer dalam beberapa tahun kebelakangan ini. Kaedah inovatif ini dicirikan oleh penggunaan berjuta-juta Gaussians 3D, yang sangat berbeza daripada kaedah medan sinaran saraf (NeRF), yang terutamanya menggunakan model berasaskan koordinat tersirat untuk memetakan koordinat spatial kepada nilai piksel. Dengan perwakilan adegan yang eksplisit dan algoritma pemaparan yang boleh dibezakan, 3DGS bukan sahaja menjamin keupayaan pemaparan masa nyata, tetapi juga memperkenalkan tahap kawalan dan pengeditan adegan yang tidak pernah berlaku sebelum ini. Ini meletakkan 3DGS sebagai penukar permainan yang berpotensi untuk pembinaan semula dan perwakilan 3D generasi akan datang. Untuk tujuan ini, kami menyediakan gambaran keseluruhan sistematik tentang perkembangan dan kebimbangan terkini dalam bidang 3DGS buat kali pertama.
 Bagaimana untuk menyelesaikan masalah ekor panjang dalam senario pemanduan autonomi?
Jun 02, 2024 pm 02:44 PM
Bagaimana untuk menyelesaikan masalah ekor panjang dalam senario pemanduan autonomi?
Jun 02, 2024 pm 02:44 PM
Semalam semasa temu bual, saya telah ditanya sama ada saya telah membuat sebarang soalan berkaitan ekor panjang, jadi saya fikir saya akan memberikan ringkasan ringkas. Masalah ekor panjang pemanduan autonomi merujuk kepada kes tepi dalam kenderaan autonomi, iaitu, kemungkinan senario dengan kebarangkalian yang rendah untuk berlaku. Masalah ekor panjang yang dirasakan adalah salah satu sebab utama yang kini mengehadkan domain reka bentuk pengendalian kenderaan autonomi pintar satu kenderaan. Seni bina asas dan kebanyakan isu teknikal pemanduan autonomi telah diselesaikan, dan baki 5% masalah ekor panjang secara beransur-ansur menjadi kunci untuk menyekat pembangunan pemanduan autonomi. Masalah ini termasuk pelbagai senario yang berpecah-belah, situasi yang melampau dan tingkah laku manusia yang tidak dapat diramalkan. "Ekor panjang" senario tepi dalam pemanduan autonomi merujuk kepada kes tepi dalam kenderaan autonomi (AVs) kes Edge adalah senario yang mungkin dengan kebarangkalian yang rendah untuk berlaku. kejadian yang jarang berlaku ini
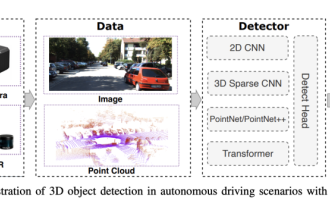 Pilih kamera atau lidar? Kajian terbaru tentang mencapai pengesanan objek 3D yang mantap
Jan 26, 2024 am 11:18 AM
Pilih kamera atau lidar? Kajian terbaru tentang mencapai pengesanan objek 3D yang mantap
Jan 26, 2024 am 11:18 AM
0. Ditulis di hadapan&& Pemahaman peribadi bahawa sistem pemanduan autonomi bergantung pada persepsi lanjutan, membuat keputusan dan teknologi kawalan, dengan menggunakan pelbagai penderia (seperti kamera, lidar, radar, dll.) untuk melihat persekitaran sekeliling dan menggunakan algoritma dan model untuk analisis masa nyata dan membuat keputusan. Ini membolehkan kenderaan mengenali papan tanda jalan, mengesan dan menjejaki kenderaan lain, meramalkan tingkah laku pejalan kaki, dsb., dengan itu selamat beroperasi dan menyesuaikan diri dengan persekitaran trafik yang kompleks. Teknologi ini kini menarik perhatian meluas dan dianggap sebagai kawasan pembangunan penting dalam pengangkutan masa depan satu. Tetapi apa yang menyukarkan pemanduan autonomi ialah memikirkan cara membuat kereta itu memahami perkara yang berlaku di sekelilingnya. Ini memerlukan algoritma pengesanan objek tiga dimensi dalam sistem pemanduan autonomi boleh melihat dan menerangkan dengan tepat objek dalam persekitaran sekeliling, termasuk lokasinya,
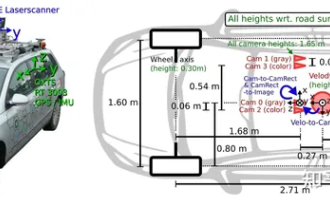 Adakah anda benar-benar menguasai penukaran sistem koordinat? Isu berbilang sensor yang tidak dapat dipisahkan daripada pemanduan autonomi
Oct 12, 2023 am 11:21 AM
Adakah anda benar-benar menguasai penukaran sistem koordinat? Isu berbilang sensor yang tidak dapat dipisahkan daripada pemanduan autonomi
Oct 12, 2023 am 11:21 AM
Artikel perintis dan utama pertama terutamanya memperkenalkan beberapa sistem koordinat yang biasa digunakan dalam teknologi pemanduan autonomi, dan cara melengkapkan korelasi dan penukaran antara mereka, dan akhirnya membina model persekitaran bersatu. Fokus di sini adalah untuk memahami penukaran daripada kenderaan kepada badan tegar kamera (parameter luaran), penukaran kamera kepada imej (parameter dalaman) dan penukaran unit imej kepada piksel. Penukaran daripada 3D kepada 2D akan mempunyai herotan, terjemahan, dsb. Perkara utama: Sistem koordinat kenderaan dan sistem koordinat badan kamera perlu ditulis semula: sistem koordinat satah dan sistem koordinat piksel Kesukaran: herotan imej mesti dipertimbangkan Kedua-dua penyahherotan dan penambahan herotan diberi pampasan pada satah imej. 2. Pengenalan Terdapat empat sistem penglihatan secara keseluruhannya: sistem koordinat satah piksel (u, v), sistem koordinat imej (x, y), sistem koordinat kamera () dan sistem koordinat dunia (). Terdapat hubungan antara setiap sistem koordinat,
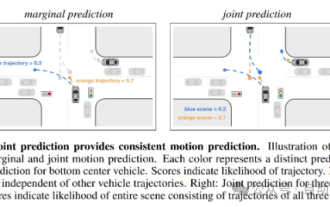 Artikel ini sudah cukup untuk anda membaca tentang pemanduan autonomi dan ramalan trajektori!
Feb 28, 2024 pm 07:20 PM
Artikel ini sudah cukup untuk anda membaca tentang pemanduan autonomi dan ramalan trajektori!
Feb 28, 2024 pm 07:20 PM
Ramalan trajektori memainkan peranan penting dalam pemanduan autonomi Ramalan trajektori pemanduan autonomi merujuk kepada meramalkan trajektori pemanduan masa hadapan kenderaan dengan menganalisis pelbagai data semasa proses pemanduan kenderaan. Sebagai modul teras pemanduan autonomi, kualiti ramalan trajektori adalah penting untuk kawalan perancangan hiliran. Tugas ramalan trajektori mempunyai timbunan teknologi yang kaya dan memerlukan kebiasaan dengan persepsi dinamik/statik pemanduan autonomi, peta ketepatan tinggi, garisan lorong, kemahiran seni bina rangkaian saraf (CNN&GNN&Transformer), dll. Sangat sukar untuk bermula! Ramai peminat berharap untuk memulakan ramalan trajektori secepat mungkin dan mengelakkan perangkap Hari ini saya akan mengambil kira beberapa masalah biasa dan kaedah pembelajaran pengenalan untuk ramalan trajektori! Pengetahuan berkaitan pengenalan 1. Adakah kertas pratonton teratur? A: Tengok survey dulu, hlm
 SIMPL: Penanda aras ramalan gerakan berbilang ejen yang mudah dan cekap untuk pemanduan autonomi
Feb 20, 2024 am 11:48 AM
SIMPL: Penanda aras ramalan gerakan berbilang ejen yang mudah dan cekap untuk pemanduan autonomi
Feb 20, 2024 am 11:48 AM
Tajuk asal: SIMPL: ASimpleandEfficientMulti-agentMotionPredictionBaselineforAutonomousDriving Paper pautan: https://arxiv.org/pdf/2402.02519.pdf Pautan kod: https://github.com/HKUST-Aerial-Robotics/SIMPL Unit pengarang: Universiti Sains Hong Kong dan Teknologi Idea Kertas DJI: Kertas kerja ini mencadangkan garis dasar ramalan pergerakan (SIMPL) yang mudah dan cekap untuk kenderaan autonomi. Berbanding dengan agen-sen tradisional
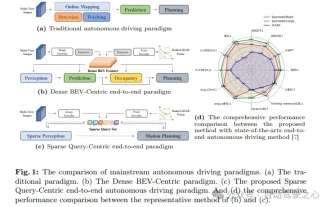 SOTA terbaharu nuScenes |. SparseAD: Pertanyaan jarang membantu pemanduan autonomi hujung ke hujung yang cekap!
Apr 17, 2024 pm 06:22 PM
SOTA terbaharu nuScenes |. SparseAD: Pertanyaan jarang membantu pemanduan autonomi hujung ke hujung yang cekap!
Apr 17, 2024 pm 06:22 PM
Ditulis di hadapan & titik permulaan Paradigma hujung ke hujung menggunakan rangka kerja bersatu untuk mencapai pelbagai tugas dalam sistem pemanduan autonomi. Walaupun kesederhanaan dan kejelasan paradigma ini, prestasi kaedah pemanduan autonomi hujung ke hujung pada subtugas masih jauh ketinggalan berbanding kaedah tugasan tunggal. Pada masa yang sama, ciri pandangan mata burung (BEV) padat yang digunakan secara meluas dalam kaedah hujung ke hujung sebelum ini menyukarkan untuk membuat skala kepada lebih banyak modaliti atau tugasan. Paradigma pemanduan autonomi hujung ke hujung (SparseAD) tertumpu carian jarang dicadangkan di sini, di mana carian jarang mewakili sepenuhnya keseluruhan senario pemanduan, termasuk ruang, masa dan tugas, tanpa sebarang perwakilan BEV yang padat. Khususnya, seni bina jarang bersatu direka bentuk untuk kesedaran tugas termasuk pengesanan, penjejakan dan pemetaan dalam talian. Di samping itu, berat
 FisheyeDetNet: algoritma pengesanan sasaran pertama berdasarkan kamera fisheye
Apr 26, 2024 am 11:37 AM
FisheyeDetNet: algoritma pengesanan sasaran pertama berdasarkan kamera fisheye
Apr 26, 2024 am 11:37 AM
Pengesanan objek ialah masalah yang agak matang dalam sistem pemanduan autonomi, antaranya pengesanan pejalan kaki adalah salah satu algoritma terawal untuk digunakan. Penyelidikan yang sangat komprehensif telah dijalankan dalam kebanyakan kertas kerja. Walau bagaimanapun, persepsi jarak menggunakan kamera fisheye untuk pandangan sekeliling agak kurang dikaji. Disebabkan herotan jejari yang besar, perwakilan kotak sempadan standard sukar dilaksanakan dalam kamera fisheye. Untuk mengurangkan perihalan di atas, kami meneroka kotak sempadan lanjutan, elips dan reka bentuk poligon am ke dalam perwakilan kutub/sudut dan mentakrifkan metrik mIOU pembahagian contoh untuk menganalisis perwakilan ini. Model fisheyeDetNet yang dicadangkan dengan bentuk poligon mengatasi model lain dan pada masa yang sama mencapai 49.5% mAP pada set data kamera fisheye Valeo untuk pemanduan autonomi



