Mencari Nombor Fibonacci Menggunakan Pengaturcaraan Dinamik

Bahagian ini menganalisis dan mereka bentuk algoritma yang cekap untuk mencari nombor Fibonacci menggunakan pengaturcaraan dinamik. Bahagian 18.3, Kajian Kes: Mengira Nombor Fibonacci, memberikan kaedah rekursif untuk mencari nombor Fibonacci, seperti berikut:

/**Kaedah untuk mencari nombor Fibonacci*/
fib panjang statik awam (indeks panjang) {
if (indeks == 0) // Kes asas
pulangkan 0;
else if (indeks == 1) // Kes asas
pulangkan 1;
else // Pengurangan dan panggilan rekursif
kembalikan fib(indeks - 1) + fib(indeks - 2);
}

Kini kita boleh membuktikan bahawa kerumitan algoritma ini ialah O(2^n). Untuk kemudahan, biarkan indeksnya n. Biarkan T(n) menandakan kerumitan untuk algoritma yang mencari fib(n) dan c menandakan masa malar untuk membandingkan indeks dengan 0 dan 1; iaitu T(1) dan T(0) ialah c. Oleh itu,

Sama seperti analisis masalah Menara Hanoi, kita boleh menunjukkan bahawa T(n) ialah O(2^n).

Walau bagaimanapun, algoritma ini tidak cekap. Adakah terdapat algoritma yang cekap untuk mencari nombor Fibonacci? Masalah dengan kaedah fib rekursif ialah kaedah itu digunakan secara berlebihan dengan hujah yang sama. Contohnya, untuk mengira fib(4), fib(3) dan fib(2) digunakan. Untuk mengira fib(3), fib(2) dan fib(1) digunakan. Ambil perhatian bahawa fib(2) digunakan secara berlebihan. Kita boleh memperbaikinya dengan mengelak daripada memanggil berulang kali kaedah fib dengan hujah yang sama. Ambil perhatian bahawa nombor Fibonacci baharu diperoleh dengan menambah dua nombor sebelumnya dalam jujukan. Jika anda menggunakan dua pembolehubah f0 dan f1 untuk menyimpan dua nombor sebelumnya, nombor baharu, f2, boleh diperolehi serta-merta dengan menambah f0 dengan f1. Sekarang anda harus mengemas kini f0 dan f1 dengan memberikan f1 kepada f0 dan menugaskan f2 kepada f1 , seperti yang ditunjukkan dalam Rajah di bawah.

Kaedah baharu dilaksanakan dalam kod di bawah.

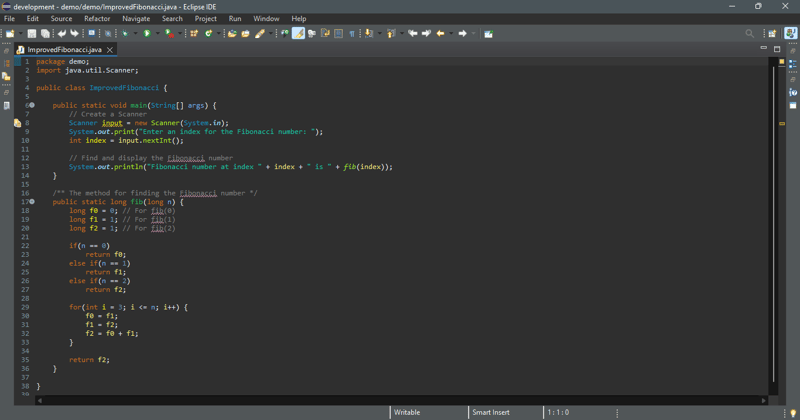
Masukkan indeks untuk nombor Fibonacci: 6
Nombor Fibonacci pada indeks 6 ialah 8

Masukkan indeks untuk nombor Fibonacci: 7
Nombor Fibonacci pada indeks 7 ialah 13

Jelas sekali, kerumitan algoritma baharu ini ialah O(n). Ini merupakan peningkatan yang luar biasa terhadap algoritma O(2^n) rekursif.

Algoritma untuk mengira nombor Fibonacci yang dibentangkan di sini menggunakan pendekatan yang dikenali sebagai pengaturcaraan dinamik. Pengaturcaraan dinamik ialah proses menyelesaikan submasalah, kemudian menggabungkan penyelesaian submasalah untuk mendapatkan penyelesaian keseluruhan. Ini secara semula jadi membawa kepada penyelesaian rekursif. Walau bagaimanapun, adalah tidak cekap untuk menggunakan rekursi, kerana submasalah bertindih. Idea utama di sebalik pengaturcaraan dinamik adalah untuk menyelesaikan setiap submasalah sekali sahaja dan menyimpan keputusan untuk submasalah untuk kegunaan kemudian bagi mengelakkan pengkomputeran berlebihan bagi submasalah.

Atas ialah kandungan terperinci Mencari Nombor Fibonacci Menggunakan Pengaturcaraan Dinamik. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!