
2192. Semua Nenek Moyang Nod dalam Graf Akiklik Berarah
Sederhana
Anda diberi integer positif n mewakili bilangan nod Graf Akiklik Berarah (DAG). Nod bernombor dari 0 hingga n - 1 (inklusif).
Anda juga diberikan tepi tatasusunan integer 2D, di mana tepi[i] = [darii, hinggai] menandakan bahawa terdapat satu arah tepi darii kei dalam graf.
Kembalikan jawapan senarai, dengan jawapan[i] ialah senarai nenek moyang nod ike, diisih dalam tertib menaik.
Nod u ialah nenek moyang nod v lain jika anda boleh mencapai v melalui set tepi.
Contoh 1:
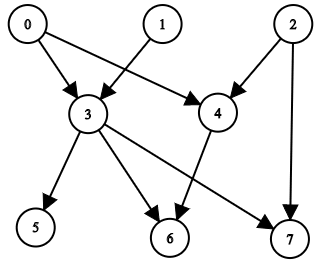
Contoh 2:
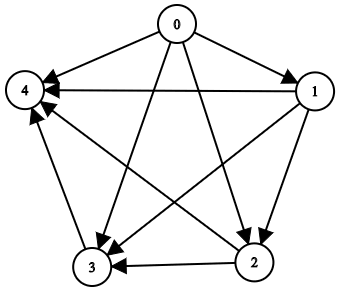
Kekangan:
Penyelesaian:
class Solution {
/**
* @param Integer $n
* @param Integer[][] $edges
* @return Integer[][]
*/
function getAncestors($n, $edges) {
$adjacencyList = array_fill(0, $n, []);
foreach ($edges as $edge) {
$from = $edge[0];
$to = $edge[1];
$adjacencyList[$to][] = $from;
}
$ancestorsList = [];
for ($i = 0; $i < $n; $i++) {
$ancestors = [];
$visited = [];
$this->findChildren($i, $adjacencyList, $visited);
for ($node = 0; $node < $n; $node++) {
if ($node == $i) continue;
if (in_array($node, $visited))
$ancestors[] = $node;
}
$ancestorsList[] = $ancestors;
}
return $ancestorsList;
}
private function findChildren($currentNode, &$adjacencyList, &$visitedNodes) {
$visitedNodes[] = $currentNode;
foreach ($adjacencyList[$currentNode] as $neighbour) {
if (!in_array($neighbour, $visitedNodes)) {
$this->findChildren($neighbour, $adjacencyList, $visitedNodes);
}
}
}
}
Pautan Kenalan
Atas ialah kandungan terperinci Semua Nenek Moyang Nod dalam Graf Akiklik Terarah. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
 Bagaimana untuk menghapuskan kod html
Bagaimana untuk menghapuskan kod html
 Maksud div dalam css
Maksud div dalam css
 Bagaimana untuk menyemak pautan mati laman web
Bagaimana untuk menyemak pautan mati laman web
 Windows 10 menjalankan pengenalan lokasi pembukaan
Windows 10 menjalankan pengenalan lokasi pembukaan
 Fungsi arahan tracert
Fungsi arahan tracert
 Mengapa saya tidak boleh membuka pinterest?
Mengapa saya tidak boleh membuka pinterest?
 Bagaimana untuk memadam elemen tatasusunan dalam JavaScript
Bagaimana untuk memadam elemen tatasusunan dalam JavaScript
 Pengenalan sintaks kelajuan
Pengenalan sintaks kelajuan




