Menyelesaikan Masalah Lapan Ratu Menggunakan Backtracking

Masalah Lapan Ratu ialah mencari penyelesaian untuk meletakkan seorang ratu dalam setiap baris pada papan catur supaya tiada dua ratu boleh menyerang satu sama lain. Masalahnya boleh diselesaikan menggunakan rekursi. Dalam bahagian ini, kami akan memperkenalkan teknik reka bentuk algoritma biasa yang dipanggil backtracking untuk menyelesaikan masalah ini. Pendekatan menjejak ke belakang mencari penyelesaian calon secara berperingkat, meninggalkan pilihan itu sebaik sahaja ia menentukan bahawa
calon tidak mungkin menjadi penyelesaian yang sah, dan kemudian mencari calon baharu.

Anda boleh menggunakan tatasusunan dua dimensi untuk mewakili papan catur. Walau bagaimanapun, oleh kerana setiap baris hanya boleh mempunyai satu ratu, adalah memadai untuk menggunakan tatasusunan satu dimensi untuk menandakan kedudukan ratu dalam baris itu. Oleh itu, anda boleh mentakrifkan tatasusunan queens sebagai:

int[] queens = int baharu[8];

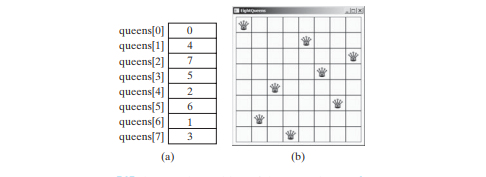
Tugaskan j kepada permaisuri[i] untuk menandakan bahawa seorang ratu diletakkan dalam baris i dan lajur j. Rajah di bawah (a) menunjukkan kandungan tatasusunan queens untuk papan catur dalam Rajah di bawah (b).

Carian bermula dari baris pertama dengan k = 0, dengan k ialah indeks baris semasa yang sedang dipertimbangkan. Algoritma menyemak sama ada ratu boleh diletakkan dalam lajur ke-j_ dalam baris untuk _j = 0, 1, ... , 7, dalam susunan ini. Carian dilaksanakan seperti berikut:

• Jika berjaya, ia terus mencari penempatan untuk seorang ratu di barisan seterusnya. Jika baris semasa ialah baris terakhir, penyelesaian ditemui.
• Jika tidak berjaya, ia berundur ke baris sebelumnya dan terus mencari peletakan baharu dalam lajur seterusnya dalam baris sebelumnya.
• Jika algoritma berundur ke baris pertama dan tidak dapat mencari peletakan baharu untuk ratu dalam baris ini, tiada penyelesaian boleh ditemui.

Kod di bawah memberikan program yang memaparkan penyelesaian untuk masalah Eight Queens.

package application;
import javafx.application.Application;
import javafx.geometry.Pos;
import javafx.stage.Stage;
import javafx.scene.Scene;
import javafx.scene.control.Label;
import javafx.scene.image.Image;
import javafx.scene.image.ImageView;
import javafx.scene.layout.GridPane;

public class EightQueens extends Application {
    public static final int SIZE = 8; // The size of the chess board
    // queens are placed at (i, queens[i])
    // -1 indicates that no queen is currently placed in the ith row
    // Initially, place a queen at (0, 0) in the 0th row
    private int[] queens = {-1, -1, -1, -1, -1, -1, -1, -1};

    @Override // Override the start method in the Application class
    public void start(Stage primaryStage) {
        search(); // Search for a solution

        // Display chess board
        GridPane chessBoard = new GridPane();
        chessBoard.setAlignment(Pos.CENTER);
        Label[][] labels = new Label[SIZE][SIZE];
        for(int i = 0; i < SIZE; i++)
            for(int j = 0; j < SIZE; j++) {
                chessBoard.add(labels[i][j] = new Label(), i, j);
                labels[i][j].setStyle("-fx-border-color: black");
                labels[i][j].setPrefSize(55, 55);
            }

        // Display queens
        Image image = new Image("file:C:/Users/Paul/development/MyJavaFX/src/application/image/lo.jpg");
        for(int i = 0; i < SIZE; i++)
            labels[i][queens[i]].setGraphic(new ImageView(image));

        // Create a scene and place it in the stage
        Scene scene = new Scene(chessBoard, 55 * SIZE, 55 * SIZE);
        primaryStage.setTitle("EightQueens"); // Set the stage title
        primaryStage.setScene(scene); // Place the scene in the stage
        primaryStage.show(); // Display the stage
    }

    public static void main(String[] args) {
        Application.launch(args);
    }

    /** Search for a solution */
    private boolean search() {
        // k - 1 indicates the number of queens placed so far
        // We are looking for a position in the kth row to place a queen
        int k = 0;
        while(k >= 0 && k < SIZE) {
            // Find a position to place a queen in the kth row
            int j = findPosition(k);
            if(j < 0) {
                queens[k] = -1;
                k--; // back track to the previous row
            } else {
                queens[k] = j;
                k++;
            }
        }

        if(k == -1)
            return false; // No solution
        else
            return true; // A solution is found
    }

    public int findPosition(int k) {
        int start = queens[k] + 1; // Search for a new placement

        for(int j =start; j < SIZE; j++) {
            if(isValid(k, j))
                return j; // (k, j) is the place to put the queen now
        }

        return -1;
    }

    /** Return true is a queen can be placed at (row, column) */
    public boolean isValid(int row, int column) {
        for(int i = 1; i <= row; i++)
            if(queens[row - i] == column // Check column
            || queens[row - i] == column - i // Check upleft diagonal
            || queens[row - i] == column + i) // Check upright diagonal
                return false; // There is a conflict
        return true; // No conflict
    }

}

Atur cara memanggil search() (baris 20) untuk mencari penyelesaian. Pada mulanya, tiada permaisuri diletakkan dalam mana-mana baris (baris 16). Carian kini bermula dari baris pertama dengan k = 0 (baris 53) dan mencari tempat untuk ratu (baris 56). Jika berjaya, letakkannya dalam baris (baris 61) dan pertimbangkan baris seterusnya (baris 62). Jika tidak berjaya, undur ke baris sebelumnya (baris 58–59).

Kaedah findPosition(k) mencari kedudukan yang mungkin untuk meletakkan ratu dalam baris k bermula dari queen[k] + 1 (baris 73 ). Ia menyemak sama ada seorang ratu boleh diletakkan di mula, mula + 1, . . . , dan 7, dalam susunan ini (baris 75–78). Jika boleh, kembalikan indeks lajur (baris 77); jika tidak, kembalikan -1 (baris 80).

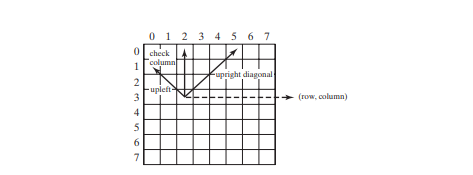
Kaedah isValid(baris, lajur) dipanggil untuk menyemak sama ada meletakkan ratu pada kedudukan yang ditentukan menyebabkan konflik dengan ratu yang diletakkan lebih awal (baris 76). Ia memastikan tiada ratu diletakkan dalam lajur yang sama (baris 86), dalam pepenjuru kiri atas (baris 87), atau dalam pepenjuru kanan atas (baris 88), seperti ditunjukkan dalam Rajah di bawah.

Atas ialah kandungan terperinci Menyelesaikan Masalah Lapan Ratu Menggunakan Backtracking. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!