
Klasifikasi ialah teknik pembelajaran diselia yang digunakan dalam pembelajaran mesin dan sains data untuk mengkategorikan data ke dalam kelas atau label yang dipratentukan. Ia melibatkan latihan model untuk menetapkan titik data input kepada salah satu daripada beberapa kategori diskret berdasarkan ciri mereka. Tujuan utama pengelasan adalah untuk meramalkan kelas atau kategori titik data baharu yang tidak kelihatan dengan tepat.
1. Klasifikasi Binari
2. Klasifikasi Berbilang Kelas
Pengelas linear ialah kategori algoritma pengelasan yang menggunakan sempadan keputusan linear untuk memisahkan kelas yang berbeza dalam ruang ciri. Mereka membuat ramalan dengan menggabungkan ciri input melalui persamaan linear, biasanya mewakili hubungan antara ciri dan label kelas sasaran. Tujuan utama pengelas linear adalah untuk mengelaskan titik data dengan cekap dengan mencari satah hiper yang membahagikan ruang ciri kepada kelas yang berbeza.
Regression Logistik ialah kaedah statistik yang digunakan untuk tugasan pengelasan binari dalam pembelajaran mesin dan sains data. Ia merupakan sebahagian daripada pengelas linear dan berbeza daripada regresi linear dengan meramalkan kebarangkalian berlakunya peristiwa melalui pemadanan data ke lengkung logistik.
1. Fungsi Logistik (Fungsi Sigmoid)
2. Persamaan Regresi Logistik
MLE digunakan untuk menganggar parameter (pekali) model regresi logistik dengan memaksimumkan kemungkinan memerhati data yang diberikan model.
Persamaan: Memaksimumkan fungsi kemungkinan log melibatkan mencari parameter yang memaksimumkan kebarangkalian memerhati data.
Fungsi kos dalam regresi logistik mengukur perbezaan antara kebarangkalian yang diramalkan dan label kelas sebenar. Matlamatnya adalah untuk meminimumkan fungsi ini untuk meningkatkan ketepatan ramalan model.
Kehilangan Log (Entropi Silang Perduaan):
Fungsi kehilangan log biasanya digunakan dalam regresi logistik untuk tugas pengelasan binari.
Kehilangan Log = -(1/n) * Σ [y * log(ŷ) + (1 - y) * log(1 - ŷ)]
di mana:
Kehilangan log menghukum ramalan yang jauh daripada label kelas sebenar, menggalakkan model menghasilkan kebarangkalian yang tepat.
Pengurangan kerugian dalam regresi logistik melibatkan pencarian nilai parameter model yang meminimumkan nilai fungsi kos. Proses ini juga dikenali sebagai pengoptimuman. Kaedah yang paling biasa untuk meminimumkan kerugian dalam regresi logistik ialah algoritma Gradient Descent.
Gradient Descent ialah algoritma pengoptimuman berulang yang digunakan untuk meminimumkan fungsi kos dalam regresi logistik. Ia melaraskan parameter model ke arah penurunan paling curam bagi fungsi kos.
Langkah Penurunan Kecerunan:
Memulakan Parameter: Mulakan dengan nilai awal untuk parameter model (cth., pekali w0, w1, ..., wn).
Kira Kecerunan: Kira kecerunan fungsi kos berkenaan dengan setiap parameter. Kecerunan ialah terbitan separa bagi fungsi kos.
Kemas Kini Parameter: Laraskan parameter dalam arah bertentangan dengan kecerunan. Pelarasan dikawal oleh kadar pembelajaran (α), yang menentukan saiz langkah yang diambil ke arah minimum.
Ulang: Ulangi proses sehingga fungsi kos menumpu kepada nilai minimum (atau bilangan lelaran yang telah ditetapkan dicapai).
Peraturan Kemas Kini Parameter:
Untuk setiap parameter wj:
wj = wj - α * (∂/∂wj) Kehilangan Log
di mana:
Terbitan separa kerugian log berkenaan dengan wj boleh dikira sebagai:
(∂/∂wj) Kehilangan Log = -(1/n) * Σ [ (yi - ŷi) * xij / (ŷi * (1 - ŷi)) ]
di mana:
Regression logistik ialah teknik yang digunakan untuk tugasan pengelasan binari, memodelkan kebarangkalian bahawa input yang diberikan tergolong dalam kelas tertentu. Contoh ini menunjukkan cara melaksanakan regresi logistik menggunakan data sintetik, menilai prestasi model dan menggambarkan sempadan keputusan.
1. Import Perpustakaan
import numpy as np import matplotlib.pyplot as plt from sklearn.model_selection import train_test_split from sklearn.linear_model import LogisticRegression from sklearn.metrics import accuracy_score, confusion_matrix, classification_report
Blok ini mengimport pustaka yang diperlukan untuk manipulasi data, plot dan pembelajaran mesin.
2. Jana Data Contoh
np.random.seed(42) # For reproducibility X = np.random.randn(1000, 2) y = (X[:, 0] + X[:, 1] > 0).astype(int)
Blok ini menjana data sampel dengan dua ciri, dengan pembolehubah sasaran y ditakrifkan berdasarkan sama ada jumlah ciri lebih besar daripada sifar, mensimulasikan senario pengelasan binari.
3. Pisahkan Set Data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
Blok ini membahagikan set data kepada set latihan dan ujian untuk penilaian model.
4. Cipta dan Latih Model Regresi Logistik
model = LogisticRegression(random_state=42) model.fit(X_train, y_train)
Blok ini memulakan model regresi logistik dan melatihnya menggunakan set data latihan.
5. Buat Ramalan
y_pred = model.predict(X_test)
Blok ini menggunakan model terlatih untuk membuat ramalan pada set ujian.
6. Nilaikan Model
accuracy = accuracy_score(y_test, y_pred)
conf_matrix = confusion_matrix(y_test, y_pred)
class_report = classification_report(y_test, y_pred)
print(f"Accuracy: {accuracy:.4f}")
print("\nConfusion Matrix:")
print(conf_matrix)
print("\nClassification Report:")
print(class_report)
Output:
Accuracy: 0.9950
Confusion Matrix:
[[ 92 0]
[ 1 107]]
Classification Report:
precision recall f1-score support
0 0.99 1.00 0.99 92
1 1.00 0.99 1.00 108
accuracy 0.99 200
macro avg 0.99 1.00 0.99 200
weighted avg 1.00 0.99 1.00 200
Blok ini mengira dan mencetak laporan ketepatan, matriks kekeliruan dan pengelasan, memberikan cerapan tentang prestasi model.
7. Visualisasikan Sempadan Keputusan
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1),
np.arange(y_min, y_max, 0.1))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.figure(figsize=(10, 8))
plt.contourf(xx, yy, Z, alpha=0.4)
plt.scatter(X[:, 0], X[:, 1], c=y, alpha=0.8)
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.title("Logistic Regression Decision Boundary")
plt.show()
Blok ini menggambarkan sempadan keputusan yang dicipta oleh model regresi logistik, menggambarkan cara model memisahkan dua kelas dalam ruang ciri.
Output:
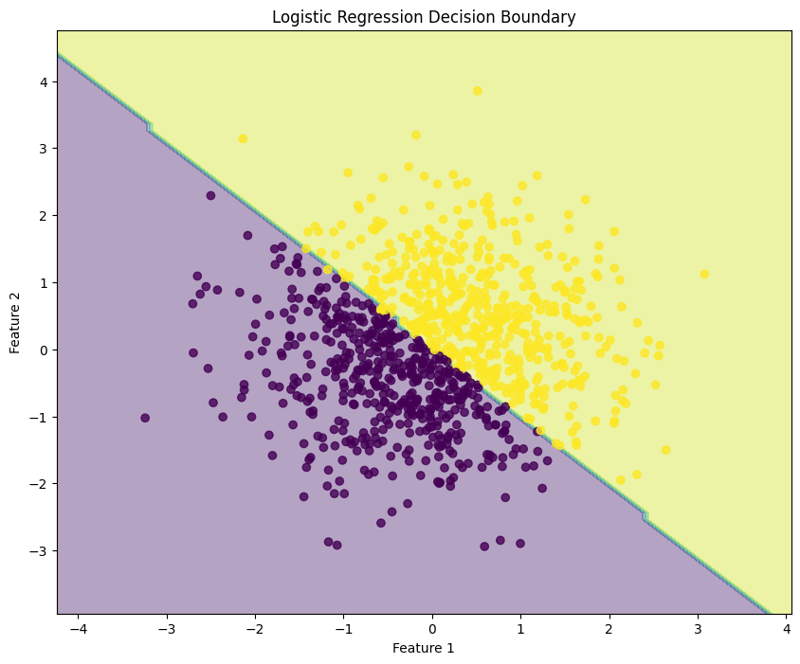
Pendekatan berstruktur ini menunjukkan cara untuk melaksanakan dan menilai regresi logistik, memberikan pemahaman yang jelas tentang keupayaannya untuk tugas klasifikasi binari. Visualisasi sempadan keputusan membantu dalam mentafsir ramalan model.
Logistic regression can also be applied to multiclass classification tasks. This example demonstrates how to implement logistic regression using synthetic data, evaluate the model's performance, and visualize the decision boundary for three classes.
1. Import Libraries
import numpy as np import matplotlib.pyplot as plt from sklearn.model_selection import train_test_split from sklearn.linear_model import LogisticRegression from sklearn.metrics import accuracy_score, confusion_matrix, classification_report
This block imports the necessary libraries for data manipulation, plotting, and machine learning.
2. Generate Sample Data with 3 Classes
np.random.seed(42) # For reproducibility
n_samples = 999 # Total number of samples
n_samples_per_class = 333 # Ensure this is exactly n_samples // 3
# Class 0: Top-left corner
X0 = np.random.randn(n_samples_per_class, 2) * 0.5 + [-2, 2]
# Class 1: Top-right corner
X1 = np.random.randn(n_samples_per_class, 2) * 0.5 + [2, 2]
# Class 2: Bottom center
X2 = np.random.randn(n_samples_per_class, 2) * 0.5 + [0, -2]
# Combine the data
X = np.vstack([X0, X1, X2])
y = np.hstack([np.zeros(n_samples_per_class),
np.ones(n_samples_per_class),
np.full(n_samples_per_class, 2)])
# Shuffle the dataset
shuffle_idx = np.random.permutation(n_samples)
X, y = X[shuffle_idx], y[shuffle_idx]
This block generates synthetic data for three classes located in different regions of the feature space.
3. Split the Dataset
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
This block splits the dataset into training and testing sets for model evaluation.
4. Create and Train the Logistic Regression Model
model = LogisticRegression(random_state=42) model.fit(X_train, y_train)
This block initializes the logistic regression model and trains it using the training dataset.
5. Make Predictions
y_pred = model.predict(X_test)
This block uses the trained model to make predictions on the test set.
6. Evaluate the Model
accuracy = accuracy_score(y_test, y_pred)
conf_matrix = confusion_matrix(y_test, y_pred)
class_report = classification_report(y_test, y_pred)
print(f"Accuracy: {accuracy:.4f}")
print("\nConfusion Matrix:")
print(conf_matrix)
print("\nClassification Report:")
print(class_report)
Output:
Accuracy: 1.0000
Confusion Matrix:
[[54 0 0]
[ 0 65 0]
[ 0 0 81]]
Classification Report:
precision recall f1-score support
0.0 1.00 1.00 1.00 54
1.0 1.00 1.00 1.00 65
2.0 1.00 1.00 1.00 81
accuracy 1.00 200
macro avg 1.00 1.00 1.00 200
weighted avg 1.00 1.00 1.00 200
This block calculates and prints the accuracy, confusion matrix, and classification report, providing insights into the model's performance.
7. Visualize the Decision Boundary
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1),
np.arange(y_min, y_max, 0.1))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.figure(figsize=(10, 8))
plt.contourf(xx, yy, Z, alpha=0.4, cmap='RdYlBu')
scatter = plt.scatter(X[:, 0], X[:, 1], c=y, cmap='RdYlBu', edgecolor='black')
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.title("Multiclass Logistic Regression Decision Boundary")
plt.colorbar(scatter)
plt.show()
This block visualizes the decision boundaries created by the logistic regression model, illustrating how the model separates the three classes in the feature space.
Output:

This structured approach demonstrates how to implement and evaluate logistic regression for multiclass classification tasks, providing a clear understanding of its capabilities and the effectiveness of visualizing decision boundaries.
Evaluating a logistic regression model involves assessing its performance in predicting binary or multiclass outcomes. Below are key methods for evaluation:
from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y_test, y_pred)
print(f'Accuracy: {accuracy:.4f}')
from sklearn.metrics import confusion_matrix
conf_matrix = confusion_matrix(y_test, y_pred)
print("\nConfusion Matrix:")
print(conf_matrix)
from sklearn.metrics import precision_score
precision = precision_score(y_test, y_pred, average='weighted')
print(f'Precision: {precision:.4f}')
from sklearn.metrics import recall_score
recall = recall_score(y_test, y_pred, average='weighted')
print(f'Recall: {recall:.4f}')
from sklearn.metrics import f1_score
f1 = f1_score(y_test, y_pred, average='weighted')
print(f'F1 Score: {f1:.4f}')
Cross-validation techniques provide a more reliable evaluation of model performance by assessing it across different subsets of the dataset.
from sklearn.model_selection import KFold, cross_val_score
kf = KFold(n_splits=5, shuffle=True, random_state=42)
scores = cross_val_score(model, X, y, cv=kf, scoring='accuracy')
print(f'Cross-Validation Accuracy: {np.mean(scores):.4f}')
from sklearn.model_selection import StratifiedKFold
skf = StratifiedKFold(n_splits=5)
scores = cross_val_score(model, X, y, cv=skf, scoring='accuracy')
print(f'Stratified K-Fold Cross-Validation Accuracy: {np.mean(scores):.4f}')
By utilizing these evaluation methods and cross-validation techniques, practitioners can gain insights into the effectiveness of their logistic regression model and its ability to generalize to unseen data.
Regularization helps mitigate overfitting in logistic regression by adding a penalty term to the loss function, encouraging simpler models. The two primary forms of regularization in logistic regression are L1 regularization (Lasso) and L2 regularization (Ridge).
Konsep: Regularisasi L2 menambah penalti yang sama dengan kuasa dua magnitud pekali kepada fungsi kehilangan.
Fungsi Kehilangan: Fungsi kehilangan yang diubah suai untuk regresi logistik Ridge dinyatakan sebagai:
Kerugian = -Σ[yi * log(ŷi) + (1 - yi) * log(1 - ŷi)] + λ * Σ(wj^2)
Di mana:
Kesan:
Konsep: Regularisasi L1 menambah penalti yang sama dengan nilai mutlak magnitud pekali kepada fungsi kehilangan.
Fungsi Kehilangan: Fungsi kehilangan yang diubah suai untuk regresi logistik Lasso boleh dinyatakan sebagai:
Kerugian = -Σ[yi * log(ŷi) + (1 - yi) * log(1 - ŷi)] + λ * Σ|wj|
Di mana:
Kesan:
Dengan menggunakan teknik regularisasi dalam regresi logistik, pengamal boleh meningkatkan generalisasi model dan mengurus tukar ganti bias-varian dengan berkesan.
Atas ialah kandungan terperinci Regresi Logistik, Klasifikasi: Pembelajaran Mesin Terselia. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
 Bagaimana untuk menyelesaikan ralat pangkalan data discuz
Bagaimana untuk menyelesaikan ralat pangkalan data discuz
 Mengapa telefon saya terus dimulakan semula?
Mengapa telefon saya terus dimulakan semula?
 windows ultimate
windows ultimate
 Perbezaan antara java dan javaee
Perbezaan antara java dan javaee
 Bagaimana untuk mempertahankan pelayan awan daripada serangan DDoS
Bagaimana untuk mempertahankan pelayan awan daripada serangan DDoS
 Bagaimana pula dengan pertukaran MEX
Bagaimana pula dengan pertukaran MEX
 Keperluan konfigurasi minimum untuk sistem win10
Keperluan konfigurasi minimum untuk sistem win10
 Penggunaan kenyataan padam
Penggunaan kenyataan padam




