
Mitchell Stern dan yang lain mencadangkan konsep prototaip persampelan spekulatif pada 2018. Pendekatan ini sejak itu telah dikembangkan dan diperhalusi lagi oleh pelbagai karya, termasuk Penyahkodan Lookhead, REST, Medusa dan EAGLE, di mana pensampelan spekulatif mempercepatkan proses inferens model bahasa besar (LLMs) dengan ketara.
Soalan penting ialah: adakah pensampelan spekulatif dalam LLM menjejaskan ketepatan model asal? Biar saya mulakan dengan jawapan: tidak.
Algoritma pensampelan spekulatif standard adalah tanpa kerugian, dan artikel ini akan membuktikannya melalui analisis dan eksperimen matematik.
Bukti matematik
Formula pensampelan spekulatif boleh ditakrifkan seperti berikut:

di mana:
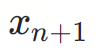 ialah token seterusnya yang akan diramalkan.
ialah token seterusnya yang akan diramalkan. Untuk kesederhanaan, kami meninggalkan syarat kebarangkalian. Sebenarnya, ? dan ? adalah pengagihan bersyarat berdasarkan urutan token awalan  .
.
Berikut ialah bukti ketidakpastian formula ini dalam kertas DeepMind:

Jika anda rasa membaca persamaan matematik terlalu membosankan, seterusnya kami akan menggambarkan proses pembuktian melalui beberapa rajah intuitif.
Ini ialah gambar rajah taburan model draf ? dan model asas ?:
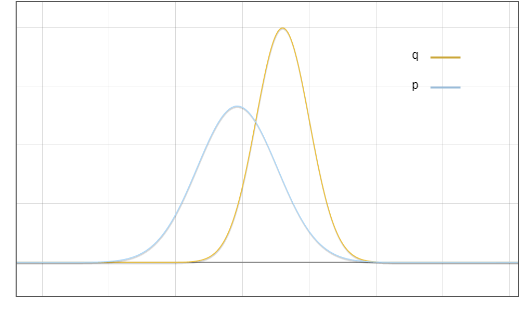
Rajah 1: Fungsi ketumpatan kebarangkalian taburan keluaran model draf p dan model asas q
Perlu diambil perhatian bahawa ini hanyalah carta yang ideal. Dalam amalan, apa yang kita kira ialah taburan diskret, yang kelihatan seperti ini:
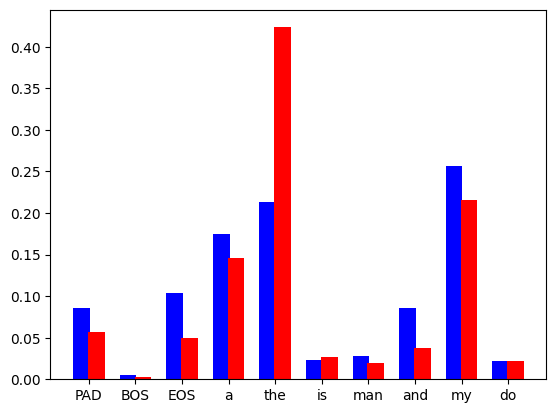
Rajah 2: Model bahasa meramalkan taburan kebarangkalian diskret bagi setiap token dalam set perbendaharaan kata, bar biru adalah daripada model draf, dan bar merah adalah dari Model asas.
Namun, demi kesederhanaan dan kejelasan, kami membincangkan masalah ini menggunakan anggaran berterusannya.
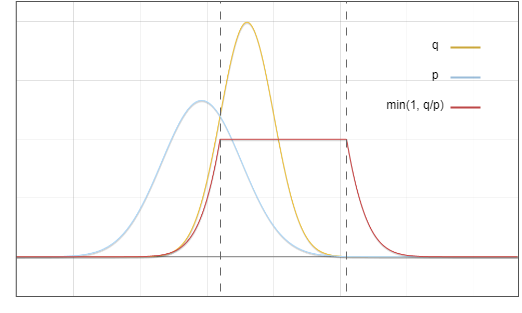
Sekarang persoalannya ialah: kami mengambil sampel daripada pengedaran , tetapi kami mahu hasil akhirnya seperti yang kami ambil daripada ? Idea utama ialah: alihkan kebarangkalian kawasan merah ke kawasan kuning:
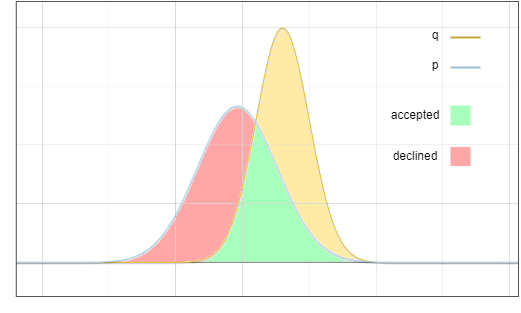
Rajah 3: Kawasan pensampelan penerimaan dan penolakan
Taburan sasaran ? Penerimaan
Terdapat dua acara bebas di cawangan ini:
Pensampelan pada pengedaran draf ? Kebarangkalian ialah ?(?)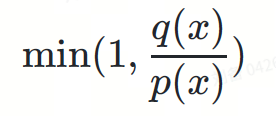
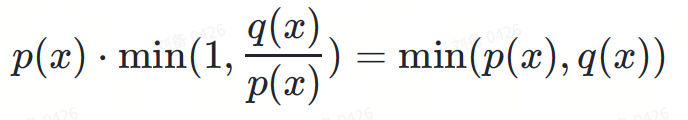
 Rajah 4: Mendarab garis biru dan merah, hasilnya adalah garis hijau dalam Rajah 6
Rajah 4: Mendarab garis biru dan merah, hasilnya adalah garis hijau dalam Rajah 6
ini adalah penolakan
II juga dua peristiwa bebas:? menolak token tertentu dalam ?, kebarangkalian ialah:
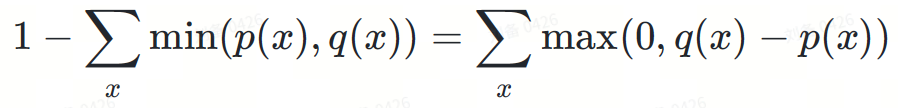 Ini adalah nilai integral, nilai itu tiada kaitan dengan token tertentu x
Ini adalah nilai integral, nilai itu tiada kaitan dengan token tertentu x ialah nombor positif dalam pengedaran ?−?( Separa) pensampelan menjana token tertentu?, kebarangkalian ialah:
Fungsi penyebutnya adalah untuk menormalkan taburan kebarangkalian untuk memastikan ketumpatan kebarangkalian kamiran sama dengan 1.
Dua item didarab bersama, dan penyebut sebutan kedua dihapuskan:
maks(0,?(?)−?(?))
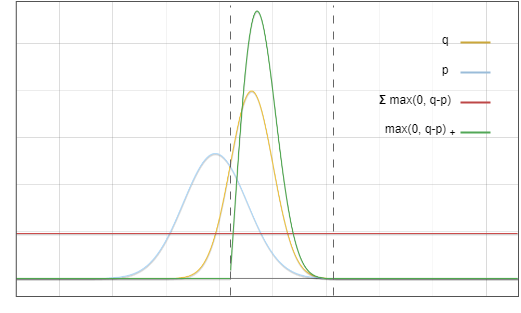
Rajah 5. Fungsi sepadan garis merah dan garis hijau dalam rajah ini Didarab bersama, hasilnya adalah sama dengan garis merah dalam Rajah 6
Mengapa kebarangkalian penolakan berlaku dinormalisasi kepada maks(0,?−?)? Walaupun ia mungkin kelihatan seperti kebetulan, pemerhatian penting di sini ialah luas kawasan merah dalam Rajah 3 adalah sama dengan luas kawasan kuning, kerana kamiran semua fungsi ketumpatan kebarangkalian adalah sama dengan 1.
Tambahkan dua bahagian I dan II: 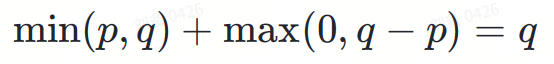
Akhirnya, kita dapat agihan sasaran ?.
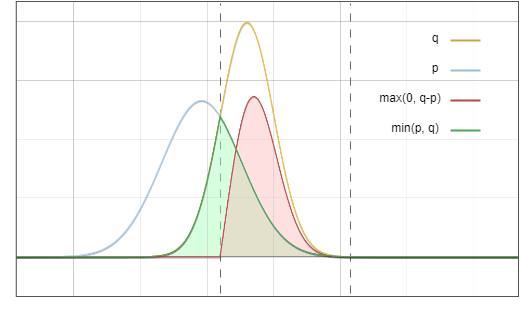
Rajah 6. Jumlah kawasan hijau dan kawasan merah adalah betul-betul sama dengan kawasan di bawah garisan kuning
Dan ini adalah matlamat kami.
Eksperimen
Walaupun kami telah membuktikan pada dasarnya bahawa pensampelan spekulatif tidak rugi, mungkin masih terdapat pepijat dalam pelaksanaan algoritma. Oleh itu, pengesahan percubaan juga perlu.
Kami menjalankan eksperimen ke atas dua kes: kaedah deterministik penyahkodan tamak dan kaedah stokastik pensampelan polinomial.
Greedy Decoding
Kami meminta LLM menjana cerpen dua kali, pertama menggunakan inferens biasa dan kemudian menggunakan pensampelan spekulatif. Suhu pensampelan ditetapkan kepada 0 untuk kedua-dua masa. Kami menggunakan pelaksanaan pensampelan spekulatif di Medusa. Berat model ialah medusa-1.0-vicuna-7b-v1.5 dan model asasnya vicuna-7b-v1.5.
Selepas larian ujian selesai, kami mendapat dua keputusan yang betul-betul sama. Teks yang dijana adalah seperti berikut:
|
Pengguna: Sila ceritakan kisah tentang seorang kesatria cyperpunk bernama PPIO mengekalkan llama yang menawan sebagai haiwan kesayangannya. Pembantu di dunia suatu ketika dahulu teknologi telah maju melangkaui impian kami yang paling liar, hiduplah seorang kesatria cyberpunk bernama PPIO adalah seorang pahlawan yang mahir, dengan peningkatan sibernetik canggih yang memberikannya kekuatan dan kepantasan yang luar biasa dan hanya . Pada suatu hari, semasa menjalankan misi, PPIO terjumpa llama yang cantik Walaupun merupakan makhluk sibernetik, PPIO mempunyai sifat lembut untuk haiwan dan dia tidak dapat menahan diri untuk menyelamatkan llama daripada bahaya yang mungkin berlaku. masuk. Mulai hari itu, llama itu mengikuti PPIO ke mana sahaja dia pergi, dan kedua-duanya menjadi kawan pantas. Llama, yang bernama Llama-ella, adalah llama yang istimewa. Ia mempunyai keupayaan unik untuk merasakan apabila seseorang berada di dalamnya bahaya dan akan mengeluarkan seruan yang kuat dan tersendiri untuk menyedarkan mereka tentang bahaya itu PPIO bersyukur atas keupayaan Llama-ella dan kedua-duanya menjadi pasukan yang tidak dapat dihalang. Bersama-sama, PPIO dan Llama-ella menempuh pelbagai cabaran, daripada memerangi penjahat sibernetik untuk menyelamatkan orang yang tidak bersalah daripada bahaya. Mereka adalah satu kuasa yang perlu diperhitungkan, dan keberanian dan kehormatan mereka adalah inspirasi kepada semua yang mengenali mereka. Kebanyakan kaedah menghasilkan semula keputusan dalam atur cara rawak menggunakan benih rawak tetap untuk mengeksploitasi determinisme penjana rawak pseudo. Walau bagaimanapun, pendekatan ini tidak sesuai untuk senario kami. Percubaan kami bergantung pada undang-undang nombor besar: diberikan sampel yang mencukupi, ralat antara taburan sebenar dan taburan teori akan menumpu kepada sifar. | Kami menyusun empat teks gesaan dan melakukan 1,000,000 lelaran pensampelan spekulatif pada token pertama yang dijana oleh LLM di bawah setiap gesaan. Berat model yang digunakan ialah
. Keputusan statistik adalah seperti berikut:
|
投機的サンプリングは、大規模な言語モデルの推論精度を損なうことはありません。厳密な数学的分析と実践的な実験を通じて、標準的な投機的サンプリング アルゴリズムの損失のない性質を実証します。数学的証明は、投機的なサンプリング公式が基礎となるモデルの元の分布をどのように保存するかを示しています。決定論的貪欲デコードや確率的多項式サンプリングを含む私たちの実験は、これらの理論的発見をさらに検証します。貪欲なデコード実験では、投機的サンプリングの有無にかかわらず同じ結果が得られましたが、多項式サンプリング実験では、多数のサンプルにわたってトークン分布の差が無視できることが示されました。 これらの結果を総合すると、投機的サンプリングにより精度を犠牲にすることなく LLM 推論を大幅に高速化し、将来的にはより効率的でアクセスしやすい AI システムへの道が開かれることが実証されました。 |
Atas ialah kandungan terperinci Adakah pensampelan spekulatif akan kehilangan ketepatan inferens model bahasa besar?. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
 Komputer menggesa penyelesaian nsiserror
Komputer menggesa penyelesaian nsiserror
 Bagaimana untuk menetapkan saiz fon html
Bagaimana untuk menetapkan saiz fon html
 Bagaimana untuk menerangi Douyin kawan rapat
Bagaimana untuk menerangi Douyin kawan rapat
 Mana satu lebih mudah, thinkphp atau laravel?
Mana satu lebih mudah, thinkphp atau laravel?
 Bagaimana untuk menyemak nilai MD5
Bagaimana untuk menyemak nilai MD5
 Pengenalan kepada penggunaan fungsi MySQL ELT
Pengenalan kepada penggunaan fungsi MySQL ELT
 Bagaimana untuk membuka kebenaran skop
Bagaimana untuk membuka kebenaran skop
 Penyemak keserasian
Penyemak keserasian
 SVN mengabaikan tetapan fail
SVN mengabaikan tetapan fail




