Kajian Kes: Masalah Bulatan Terhubung

Masalah bulatan bersambung adalah untuk menentukan sama ada semua bulatan dalam satah dua dimensi disambungkan. Masalah ini boleh diselesaikan menggunakan traversal depth-first. Algoritma DFS mempunyai banyak aplikasi. Bahagian ini menggunakan algoritma DFS untuk menyelesaikan masalah bulatan bersambung.

Dalam masalah bulatan bersambung, anda menentukan sama ada semua bulatan dalam satah dua dimensi disambungkan. Jika semua bulatan disambungkan, ia dicat sebagai bulatan terisi, seperti yang ditunjukkan dalam Rajah di bawah (a). Jika tidak, ia tidak diisi, seperti yang ditunjukkan dalam Rajah di bawah (b).

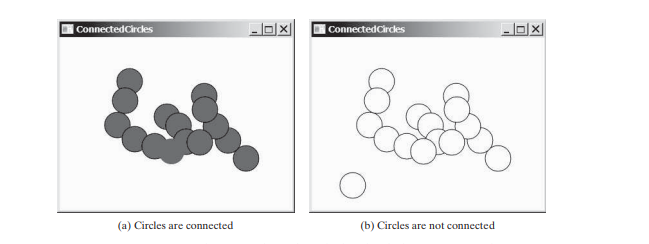
Kami akan menulis program yang membolehkan pengguna membuat bulatan dengan mengklik tetikus di kawasan kosong yang tidak diliputi oleh bulatan pada masa ini. Apabila bulatan ditambah, bulatan dicat semula diisi jika ia disambungkan atau tidak diisi sebaliknya.

Kami akan membuat graf untuk memodelkan masalah. Setiap bulatan ialah bucu dalam graf. Dua bulatan disambungkan jika ia bertindih. Kami menggunakan DFS dalam graf dan jika semua bucu ditemui dalam carian mendalam-pertama, graf disambungkan.

Atur cara diberikan dalam kod di bawah.

import javafx.application.Application;
import javafx.geometry.Point2D;
import javafx.scene.Node;
import javafx.scene.Scene;
import javafx.scene.layout.Pane;
import javafx.scene.paint.Color;
import javafx.scene.shape.Circle;
import javafx.stage.Stage;

public class ConnectedCircles extends Application {
    @Override // Override the start method in the Application class
    public void start(Stage primaryStage) {
        // Create a scene and place it in the stage
        Scene scene = new Scene(new CirclePane(), 450, 350);
        primaryStage.setTitle("ConnectedCircles"); // Set the stage title
        primaryStage.setScene(scene); // Place the scene in the stage
        primaryStage.show(); // Display the stage
    }

    public static void main(String[] args) {
        Application.launch(args);
    }

    /** Pane for displaying circles */
    class CirclePane extends Pane {
        public CirclePane() {
            this.setOnMouseClicked(e -> {
                if (!isInsideACircle(new Point2D(e.getX(), e.getY()))) {
                    // Add a new circle
                    getChildren().add(new Circle(e.getX(), e.getY(), 20));
                    colorIfConnected();
                }
            });
        }

        /** Returns true if the point is inside an existing circle */
        private boolean isInsideACircle(Point2D p) {
            for (Node circle: this.getChildren())
                if (circle.contains(p))
                    return true;

            return false;
        }

        /** Color all circles if they are connected */
        private void colorIfConnected() {
            if (getChildren().size() == 0)
                return; // No circles in the pane

            // Build the edges
            java.util.List<AbstractGraph.Edge> edges = new java.util.ArrayList<>();
            for (int i = 0; i < getChildren().size(); i++)
                for (int j = i + 1; j < getChildren().size(); j++)
                    if (overlaps((Circle)(getChildren().get(i)), (Circle)(getChildren().get(j)))) {
                        edges.add(new AbstractGraph.Edge(i, j));
                        edges.add(new AbstractGraph.Edge(j, i));
                    }

            // Create a graph with circles as vertices
            Graph<Node> graph = new UnweightedGraph<>((java.util.List<Node>)getChildren(), edges);
            AbstractGraph<Node>.Tree tree = graph.dfs(0); // a DFS tree
            boolean isAllCirclesConnected = getChildren().size() == tree.getNumberOfVerticesFound();

            for (Node circle: getChildren()) {
                if (isAllCirclesConnected) { // All circles are connected
                    ((Circle)circle).setFill(Color.RED);
                }
                else {
                    ((Circle)circle).setStroke(Color.BLACK);
                    ((Circle)circle).setFill(Color.WHITE);
                }
            }
        }
    }

    public static boolean overlaps(Circle circle1, Circle circle2) {
        return new Point2D(circle1.getCenterX(), circle1.getCenterY()).distance(circle2.getCenterX(), circle2.getCenterY()) <= circle1.getRadius() + circle2.getRadius();
    }
}

Kelas JavaFX Lingkaran mengandungi medan data x, y dan jejari, yang menentukan lokasi pusat dan jejari bulatan . Ia juga mentakrifkan mengandungi untuk menguji jika titik berada dalam bulatan. Kaedah tindih (baris 76–80) menyemak sama ada dua bulatan bertindih.

Apabila pengguna mengklik tetikus di luar mana-mana kalangan sedia ada, bulatan baharu dibuat berpusat pada titik tetikus dan bulatan itu ditambahkan pada anak tetingkap (baris 26).

Untuk mengesan sama ada bulatan disambungkan, atur cara membina graf (baris 46–59). Bulatan ialah bucu graf. Tepi dibina dalam baris 49–55. Dua bucu bulatan disambungkan jika ia bertindih (baris 51). DFS graf menghasilkan pokok (baris 60). getNumberOfVerticesFound() pokok itu mengembalikan bilangan bucu yang dicari. Jika ia sama dengan bilangan bulatan, semua kalangan disambungkan (baris 61–62).

Atas ialah kandungan terperinci Kajian Kes: Masalah Bulatan Terhubung. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!