Pemodelan Graf

Antara muka Graf mentakrifkan operasi biasa untuk graf. Rangka Kerja Koleksi Java berfungsi sebagai contoh yang baik untuk mereka bentuk struktur data yang kompleks. Ciri biasa struktur data ditakrifkan dalam antara muka (cth., Koleksi, Tetapkan, Senarai, Baris Gilir), seperti yang ditunjukkan dalam Rajah 20.1. Kelas abstrak (cth., AbstractCollection, AbstractSet, AbstractList) melaksanakan sebahagian antara muka. Kelas konkrit (cth., HashSet, LinkedHashSet, TreeSet, ArrayList, LinkedList>) menyediakan pelaksanaan konkrit. Corak reka bentuk ini berguna untuk memodelkan graf. Kami akan mentakrifkan antara muka bernama Graf yang mengandungi semua operasi biasa graf dan kelas abstrak bernama Graf Abstrak yang sebahagiannya melaksanakan antara muka Graf. Banyak graf konkrit boleh ditambah pada reka bentuk. Sebagai contoh, kami akan mentakrifkan graf sedemikian bernama UnweightedGraph dan WeightedGraph. Hubungan antara muka dan kelas ini digambarkan dalam Rajah di bawah.

Apakah operasi biasa untuk graf? Secara umum, anda perlu mendapatkan bilangan bucu dalam graf, dapatkan semua bucu dalam graf, dapatkan objek bucu dengan indeks tertentu, dapatkan indeks bucu dengan nama yang ditentukan, dapatkan jiran untuk bucu, dapatkan darjah untuk bucu, kosongkan graf, tambah bucu baharu, tambah tepi baharu, lakukan carian mendalam-dahulu dan lakukan carian luas-dahulu. Carian mendalam-dahulu dan carian luas-dahulu akan diperkenalkan di bahagian seterusnya. Rajah di bawah menggambarkan kaedah ini dalam rajah UML.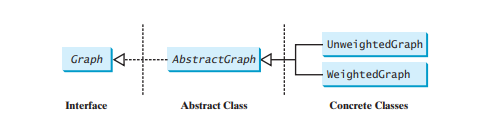

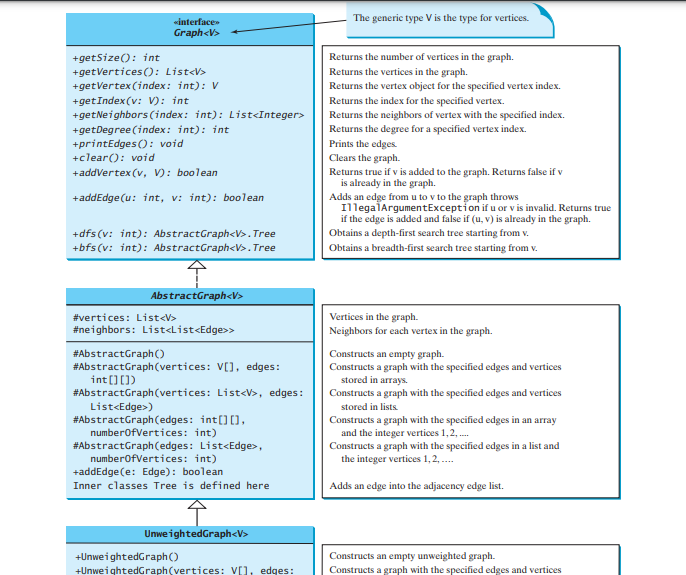
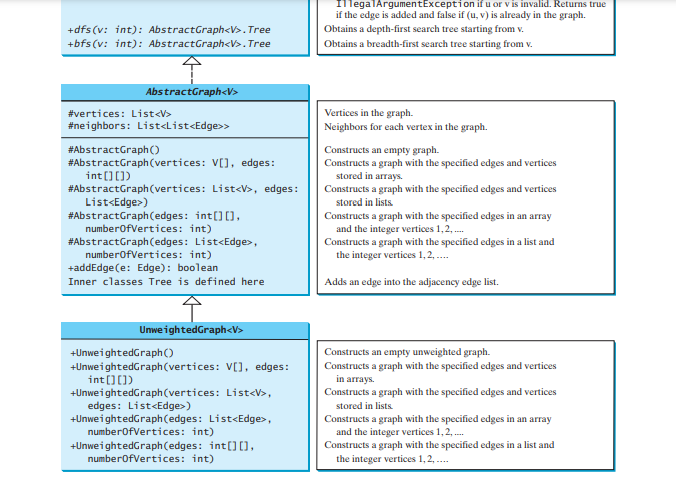Graf Abstrak

tidak memperkenalkan sebarang kaedah baharu. Senarai bucu dan senarai bersebelahan tepi ditakrifkan dalam kelas

Graf Abstrak. Dengan medan data ini, adalah memadai untuk melaksanakan semua kaedah yang ditakrifkan dalam antara muka Graf. Untuk kemudahan, kami menganggap graf ialah graf ringkas, iaitu, bucu tidak mempunyai tepi pada dirinya sendiri dan tiada tepi selari dari bucu u hingga v. Graf Abstrak

melaksanakan semua kaedah daripada

Graf, dan ia tidak memperkenalkan sebarang kaedah baharu kecuali kaedah addEdge(edge) yang mudah yang menambah Tepi membantah senarai tepi bersebelahan. UnweightedGraph hanya memanjangkan AbstractGraph dengan lima pembina untuk mencipta contoh Graf konkrit. Anda boleh membuat graf dengan sebarang jenis bucu. Setiap bucu dikaitkan dengan indeks, yang sama dengan indeks bucu dalam senarai bucu. Jika anda membuat graf tanpa menyatakan bucu, bucu adalah sama dengan indeksnya.

Kelas

Graf Abstrak

melaksanakan semua kaedah dalam antara muka

Graf. Jadi mengapa ia ditakrifkan sebagai abstrak? Pada masa hadapan, anda mungkin perlu menambah kaedah baharu pada antara muka Graf yang tidak boleh dilaksanakan dalam Graf Abstrak. Untuk menjadikan kelas mudah diselenggara, adalah wajar untuk mentakrifkan kelas Graf Abstrak sebagai abstrak.

Anggap semua antara muka dan kelas ini tersedia. Kod di bawah memberikan program ujian yang mencipta graf dalam Rajah di atas dan graf lain untuk yang dalam Rajah di bawah (a).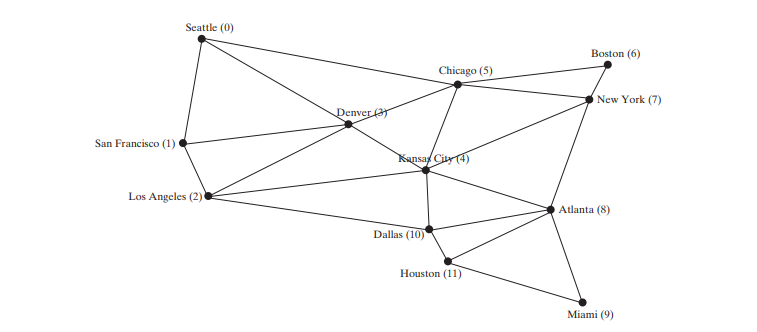

Bilangan bucu dalam graf1: 12

Puncak dengan indeks 1 ialah San Francisco

public class TestGraph {

    public static void main(String[] args) {
        String[] vertices = {"Seattle", "San Francisco", "Los Angeles", "Denver", "Kansas City", "Chicago", "Boston", "New York", "Atlanta", "Miami", "Dallas", "Houston"};

        // Edge array for graph
        int[][] edges = {
                {0, 1}, {0, 3}, {0, 5},
                {1, 0}, {1, 2}, {1, 3},
                {2, 1}, {2, 3}, {2, 4}, {2, 10},
                {3, 0}, {3, 1}, {3, 2}, {3, 4}, {3, 5},
                {4, 2}, {4, 3}, {4, 5}, {4, 7}, {4, 8}, {4, 10},
                {5, 0}, {5, 3}, {5, 4}, {5, 6}, {5, 7},
                {6, 5}, {6, 7},
                {7, 4}, {7, 5}, {7, 6}, {7, 8},
                {8, 4}, {8, 7}, {8, 9}, {8, 10}, {8, 11},
                {9, 8}, {9, 11},
                {10, 2}, {10, 4}, {10, 8}, {10, 11},
                {11, 8}, {11, 9}, {11, 10}
        };

        Graph<String> graph1 = new UnweightedGraph<>(vertices, edges);
        System.out.println("The number of vertices in graph1: " + graph1.getSize());
        System.out.println("The vertex with index 1 is " + graph1.getVertex(1));
        System.out.println("The index for Miami is " + graph1.getIndex("Miami"));
        System.out.println("The edges for graph1:");
        graph1.printEdges();

        // List of Edge objects for graph
        String[] names = {"Peter", "Jane", "Mark", "Cindy", "Wendy"};
        java.util.ArrayList<AbstractGraph.Edge> edgeList = new java.util.ArrayList<>();
        edgeList.add(new AbstractGraph.Edge(0, 2));
        edgeList.add(new AbstractGraph.Edge(1, 2));
        edgeList.add(new AbstractGraph.Edge(2, 4));
        edgeList.add(new AbstractGraph.Edge(3, 4));
        // Create a graph with 5 vertices
        Graph<String> graph2 = new UnweightedGraph<>(java.util.Arrays.asList(names), edgeList);
        System.out.println("\nThe number of vertices in graph2: " + graph2.getSize());
        System.out.println("Te edges for graph2:");
        graph2.printEdges();
    }

}

Indeks untuk Miami ialah 9

Tepi untuk graf1:
Seattle (0): (0, 1) (0, 3) (0, 5)
San Francisco (1): (1, 0) (1, 2) (1, 3)
Los Angeles (2): (2, 1) (2, 3) (2, 4) (2, 10)
Denver (3): (3, 0) (3, 1) (3, 2) (3, 4) (3, 5)
Kansas City (4): (4, 2) (4, 3) (4, 5) (4, 7) (4, 8) (4, 10)
Chicago (5): (5, 0) (5, 3) (5, 4) (5, 6) (5, 7)
Boston (6): (6, 5) (6, 7)
New York (7): (7, 4) (7, 5) (7, 6) (7, 8)
Atlanta (8): (8, 4) (8, 7) (8, 9) (8, 10) (8, 11)
Miami (9): (9, 8) (9, 11)
Dallas (10): (10, 2) (10, 4) (10, 8) (10, 11)
Houston (11): (11, 8) (11, 9) (11, 10)

The number of vertices in graph2: 5
The edges for graph2:
Peter (0): (0, 2)
Jane (1): (1, 2)
Mark (2): (2, 4)
Cindy (3): (3, 4)
Wendy (4):

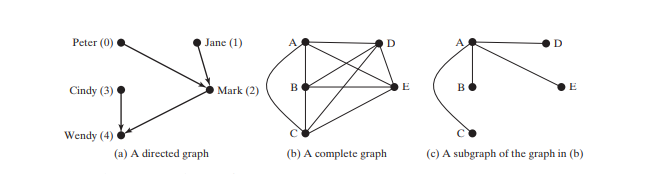
The program creates graph1 for the graph in Figure 28.1 in lines 3–23. The vertices for graph1 are defined in lines 3–5. The edges for graph1 are defined in 8–21. The edges are represented using a two-dimensional array. For each row i in the array, edges[i][0] and edges[i][1] indicate that there is an edge from vertex edges[i][0] to vertex edges[i][1]. For example, the first row, {0, 1}, represents the edge from vertex 0 (edges[0][0]) to vertex 1 (edges[0][1]). The row {0, 5} represents the edge from vertex 0 (edges[2][0]) to vertex 5 (edges[2][1]). The graph is created in line 23. Line 31 invokes the printEdges() method on graph1 to display all edges in graph1.

The program creates graph2 for the graph in Figure 28.3a in lines 34–43. The edges for graph2 are defined in lines 37–40. graph2 is created using a list of Edge objects in line 43. Line 47 invokes the printEdges() method on graph2 to display all edges in graph2.

Note that both graph1 and graph2 contain the vertices of strings. The vertices are associated with indices 0, 1, . . . , n-1. The index is the location of the vertex in vertices. For example, the index of vertex Miami is 9.

Now we turn our attention to implementing the interface and classes. The codes below give the Graph interface, the AbstractGraph class, and the UnweightedGraph class, respectively.

public interface Graph<V> {
    /** Return the number of vertices in the graph */
    public int getSize();

    /** Return the vertices in the graph */
    public java.util.List<V> getVertices();

    /** Return the object for the specified vertex index */
    public V getVertex(int index);

    /** Return the index for the specified vertex object */
    public int getIndex(V v);

    /** Return the neighbors of vertex with the specified index */
    public java.util.List<Integer> getNeighbors(int index);

    /** Return the degree for a specified vertex */
    public int getDegree(int v);

    /** Print the edges */
    public void printEdges();

    /** Clear the graph */
    public void clear();

    /** Add a vertex to the graph */
    public void addVertex(V vertex);

    /** Add an edge to the graph */
    public void addEdge(int u, int v);

    /** Obtain a depth-first search tree starting from v */
    public AbstractGraph<V>.Tree dfs(int v);

    /** Obtain a breadth-first search tree starting from v */
    public AbstractGraph<V>.Tree bfs(int v);
}

import java.util.*;

public abstract class AbstractGraph<V> implements Graph<V> {
    protected List<V> vertices = new ArrayList<>(); // Store vertices
    protected List<List<Edge>> neighbors = new ArrayList<>(); // Adjacency lists

    /** Construct an empty graph */
    protected AbstractGraph() {}

    /** Construct a graph from vertices and edges stored in arrays */
    protected AbstractGraph(V[] vertices, int[][] edges) {
        for(int i = 0; i < vertices.length; i++)
            addVertex(vertices[i]);

        createAdjacencyLists(edges, vertices.length);
    }

    /** Construct a graph from vertices and edges stored in List */
    protected AbstractGraph(List<V> vertices, List<Edge> edges) {
        for(int i = 0; i < vertices.size(); i++)
            addVertex(vertices.get(i));

        createAdjacencyLists(edges, vertices.size());
    }

    /** Construct a graph for integer vertices 0, 1, 2 and edge list */
    protected AbstractGraph(List<Edge> edges, int numberOfVertices) {
        for(int i = 0; i < numberOfVertices; i++)
            addVertex((V)(new Integer(i))); // vertices is {0, 1, ...}

        createAdjacencyLists(edges, numberOfVertices);
    }

    /** Construct a graph from integer vertices 0, 1, and edge array */
    protected AbstractGraph(int[][] edges, int numberOfVertices) {
        for(int i = 0; i < numberOfVertices; i++)
            addVertex((V)(new Integer(i))); // vertices is {0, 1, ...}

        createAdjacencyLists(edges, numberOfVertices);
    }

    /** Create adjacency lists for each vertex */
    private void createAdjacencyLists(int[][] edges, int numberOfVertices) {
        for(int i = 0; i < edges.length; i++) {
            addEdge(edges[i][0], edges[i][1]);
        }
    }

    /** Create adjacency lists for each vertex */
    private void createAdjacencyLists(List<Edge> edges, int numberOfVertices) {
        for(Edge edge: edges) {
            addEdge(edge.u, edge.v);
        }
    }

    @Override /** Return the number of vertices in the graph */
    public int getSize() {
        return vertices.size();
    }

    @Override /** Return the vertices in the graph */
    public List<V> getVertices() {
        return vertices;
    }

    @Override /** Return the object for the specified vertex */
    public V getVertex(int index) {
        return vertices.get(index);
    }

    @Override /** Return the index for the specified vertex object */
    public int getIndex(V v) {
        return vertices.indexOf(v);
    }

    @Override /** Return the neighbors of the specified vertex */
    public List<Integer> getNeighbors(int index) {
        List<Integer> result = new ArrayList<>();
        for(Edge e: neighbors.get(index))
            result.add(e.v);

        return result;
    }

    @Override /** Return the degree for a specified vertex */
    public int getDegree(int v) {
        return neighbors.get(v).size();
    }

    @Override /** Print the edges */
    public void printEdges() {
        for(int u = 0; u < neighbors.size(); u++) {
            System.out.print(getVertex(u) + " (" + u + "): ");
            for(Edge e: neighbors.get(u)) {
                System.out.print("(" + getVertex(e.u) + ", " + getVertex(e.v) + ") ");
            }
            System.out.println();
        }
    }

    @Override /** Clear the graph */
    public void clear() {
        vertices.clear();
        neighbors.clear();
    }

    @Override /** Add a vertex to the graph */
    public void addVertex(V vertex) {
        if(!vertices.contains(vertex)) {
            vertices.add(vertex);
            neighbors.add(new ArrayList<Edge>());
        }
    }

    /** Add an edge to the graph */
    protected boolean addEdge(Edge e) {
        if(e.u < 0 || e.u > getSize() - 1)
            throw new IllegalArgumentException("No such index: " + e.u);

        if(e.v < 0 || e.v > getSize() - 1)
            throw new IllegalArgumentException("No such index: " + e.v);

        if(!neighbors.get(e.u).contains(e)) {
            neighbors.get(e.u).add(e);
            return true;
        }
        else {
            return false;
        }
    }

    @Override /** Add an edge to the graph */
    public void addEdge(int u, int v) {
        addEdge(new Edge(u, v));
    }

    /** Edge inner class inside the AbstractGraph class */
    public static class Edge {
        public int u; // Starting vertex of the edge
        public int v; // Ending vertex of the edge

        /** Construct an edge for (u, v) */
        public Edge(int u, int v) {
            this.u = u;
            this.v = v;
        }

        public boolean equals(Object o) {
            return u == ((Edge)o).u && v == ((Edge)o).v;
        }
    }

    @Override /** Obtain a DFS tree starting from vertex v */
    public Tree dfs(int v) {
        List<Integer> searchOrder = new ArrayList<>();
        int[] parent = new int[vertices.size()];
        for(int i = 0; i < parent.length; i++)
            parent[i] = -1; // Initialize parent[i] to -1

        // Mark visited vertices
        boolean[] isVisited = new boolean[vertices.size()];

        // Recursively search
        dfs(v, parent, searchOrder, isVisited);

        // Return a search tree
        return new Tree(v, parent, searchOrder);
    }

    /** Recursive method for DFS search */
    private void dfs(int u, int[] parent, List<Integer> searchOrder, boolean[] isVisited) {
        // Store the visited vertex
        searchOrder.add(u);
        isVisited[u] = true; // Vertex v visited

        for(Edge e: neighbors.get(u)) {
            if(!isVisited[e.v]) {
                parent[e.v] = u; // The parent of vertex e.v is u
                dfs(e.v, parent, searchOrder, isVisited); // Recursive search
            }
        }
    }

    @Override /** Starting bfs search from vertex v */
    public Tree bfs(int v) {
        List<Integer> searchOrder = new ArrayList<>();
        int[] parent = new int[vertices.size()];
        for(int i = 0; i < parent.length; i++)
            parent[i] = -1; // Initialize parent[i] to -1

        java.util.LinkedList<Integer> queue = new java.util.LinkedList<>(); // list used as queue
        boolean[] isVisited = new boolean[vertices.size()];
        queue.offer(v); // Enqueue v
        isVisited[v] = true; // Mark it visited

        while(!queue.isEmpty()) {
            int u = queue.poll(); // Dequeue to u
            searchOrder.add(u); // u searched
            for(Edge e: neighbors.get(u)) {
                if(!isVisited[e.v]) {
                    queue.offer(e.v); // Enqueue w
                    parent[e.v] = u; // The parent of w is u
                    isVisited[e.v] = true; // Mark it visited
                }
            }
        }

        return new Tree(v, parent, searchOrder);
    }

    /** Tree inner class inside the AbstractGraph class */
    public class Tree {
        private int root; // The root of the tree
        private int[] parent; // Store the parent of each vertex
        private List<Integer> searchOrder; // Store the search order

        /** Construct a tree with root, parent, and searchOrder */
        public Tree(int root, int[] parent, List<Integer> searchOrder) {
            this.root = root;
            this.parent = parent;
            this.searchOrder = searchOrder;
        }

        /** Return the root of the tree */
        public int getRoot() {
            return root;
        }

        /** Return the parent of vertex v */
        public int getParent(int v) {
            return parent[v];
        }

        /** Return an array representing search order */
        public List<Integer> getSearchOrder() {
            return searchOrder;
        }

        /** Return number of vertices found */
        public int getNumberOfVerticesFound() {
            return searchOrder.size();
        }

        /** Return the path of vertices from a vertex to the root */
        public List<V> getPath(int index) {
            ArrayList<V> path = new ArrayList<>();

            do {
                path.add(vertices.get(index));
                index = parent[index];
            }
            while(index != -1);

            return path;
        }

        /** Print a path from the root vertex v */
        public void printPath(int index) {
            List<V> path = getPath(index);
            System.out.print("A path from " + vertices.get(root) + " to " + vertices.get(index) + ": ");
            for(int i = path.size() - 1; i >= 0; i--)
                System.out.print(path.get(i) + " ");
        }

        /** Print the whole tree */
        public void printTree() {
            System.out.println("Root is: " + vertices.get(root));
            System.out.print("Edges: ");
            for(int i = 0; i < parent.length; i++) {
                if(parent[i] != -1) {
                    // Display an edge
                    System.out.print("(" + vertices.get(parent[i]) + "' " + vertices.get(i) + ") ");
                }
            }
            System.out.println();
        }
    }
}

import java.util.*;

public class UnweightedGraph<V> extends AbstractGraph<V> {
    /** Construct an empty graph */
    public UnweightedGraph() {}

    /** Construct a graph from vertices and edges stored in arrays */
    public UnweightedGraph(V[] vertices, int[][] edges) {
        super(vertices, edges);
    }
    /** Construct a graph from vertices and edges stored in List */
    public UnweightedGraph(List<V> vertices, List<Edge> edges) {
        super(vertices, edges);
    }

    /** Construct a graph for integer vertices 0, 1, 2, and edge list */
    public UnweightedGraph(List<Edge> edges, int numberOfVertices) {
        super(edges, numberOfVertices);
    }

    /** Construct a graph from integer vertices 0, 1, and edge array */
    public UnweightedGraph(int[][] edges, int numberOfVertices) {
        super(edges, numberOfVertices);
    }
}

The code in the Graph interface and the UnweightedGraph class are straightforward. Let us digest the code in the AbstractGraph class.

The AbstractGraph class defines the data field vertices (line 4) to store vertices and neighbors (line 5) to store edges in adjacency lists. neighbors.get(i) stores all edges adjacent to vertex i. Four overloaded constructors are defined in lines 9–42 to create a default graph, or a graph from arrays or lists of edges and vertices. The createAdjacencyLists(int[][] edges, int numberOfVertices) method creates adjacency lists from edges in an array (lines 45–50). The createAdjacencyLists(List edges, int numberOfVertices) method creates adjacency lists from edges in a list (lines 53–58).

The getNeighbors(u) method (lines 81–87) returns a list of vertices adjacent to vertex u. The clear() method (lines 106–110) removes all vertices and edges from the graph. The addVertex(u) method (lines 112–122) adds a new vertex to vertices and returns true. It returns false if the vertex is already in the graph (line 120).

The addEdge(e) method (lines 124–139) adds a new edge the adjacency edge list and returns true. It returns false if the edge is already in the graph. This method may throw IllegalArgumentException if the edge is invalid (lines 126–130).

The printEdges() method (lines 95–104) displays all vertices and edges adjacent to each vertex.

The code in lines 164–293 gives the methods for finding a depth-first search tree and a breadth-first search tree, which will be introduced in Depth-First Search (DFS) and Breadth-First Search (BFS), respectively.

Atas ialah kandungan terperinci Pemodelan Graf. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!