masalah subarray maks dan algoritma kadane

Masalah subarray maks dan sejarahnya

Pada akhir 1970-an, ahli matematik Sweden Ulf Grenander telah membincangkan masalah: bagaimana anda boleh menganalisis tatasusunan data imej 2D dengan lebih cekap daripada kekerasan? Komputer kemudiannya perlahan dan gambar adalah besar berbanding dengan RAM. Untuk memburukkan lagi keadaan, dalam senario terburuk, kekerasan mengambil masa O(n^6) (kerumitan masa sekstik).

Mula-mula, Grenandier memudahkan soalan: Memandangkan hanya tatasusunan nombor satu dimensi, bagaimanakah anda boleh mencari subray bersebelahan dengan jumlah terbesar dengan paling cekap?

Brute Force: Pendekatan Naif dengan Kerumitan Masa Kubik

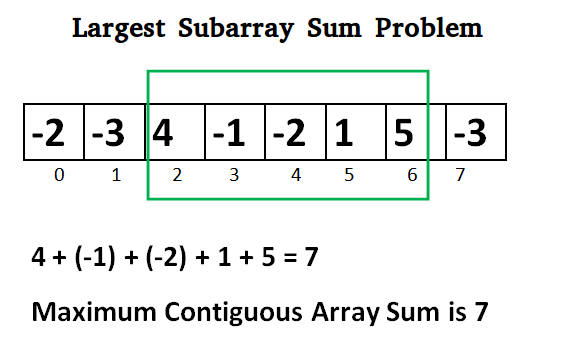
Brute force, ia akan mengambil separuh masa untuk menganalisis tatasusunan 1D sebagai tatasusunan 2D, jadi O(n^3) untuk memeriksa setiap kombinasi yang mungkin (kerumitan masa padu).

def max_subarray_brute_force(arr):
    max_sum = arr[0] # assumes arr has a length

    # iterate over all possible subarrays
    for i in range(len(arr)):
        for j in range(i, len(arr)):
            current_sum = 0
            # sum the elements of the subarray arr[i:j+1]
            for k in range(i, j + 1):
                current_sum += arr[k]
            # update max_sum if the current sum is greater
            max_sum = max(max_sum, current_sum)

    return max_sum

print(max_subarray_brute_force([-2, -3, 4, -1, -2, 1, 5, -3]), "== 7")

Pengoptimuman O(n²) Grenander: Satu Langkah Ke Hadapan

Grenander menambah baiknya kepada penyelesaian O(n^2). Saya tidak dapat mencari kodnya dalam penyelidikan saya, tetapi tekaan saya ialah dia hanya menyingkirkan gelung paling dalam yang menjumlahkan semua nombor antara dua indeks. Sebaliknya, kita boleh mengekalkan jumlah larian semasa melelakan ke atas subarray, sekali gus mengurangkan bilangan gelung daripada tiga kepada dua.

def max_subarray_optimized(arr):
    max_sum = arr[0]  # assumes arr has a length

    # iterate over all possible starting points of the subarray
    for i in range(len(arr)):
        current_sum = 0
        # sum the elements of the subarray starting from arr[i]
        for j in range(i, len(arr)):
            current_sum += arr[j]
            # update max_sum if the current sum is greater
            max_sum = max(max_sum, current_sum)

    return max_sum

Perpecahan dan Penaklukan Shamos: Memisahkan Masalah untuk O(n log n)

Grenander menunjukkan masalah itu kepada saintis komputer Michael Shamos. Shamos memikirkannya selama satu malam dan menghasilkan kaedah bahagi dan takluk iaitu O(n log n).

Ia agak bijak. Ideanya adalah untuk membahagikan tatasusunan kepada dua bahagian, kemudian cari secara rekursif jumlah subarray maksimum untuk setiap separuh serta subarray yang melintasi titik tengah.

def max_crossing_sum(arr, left, mid, right):
    # left of mid
    left_sum = float('-inf')
    current_sum = 0
    for i in range(mid, left - 1, -1):
        current_sum += arr[i]
        left_sum = max(left_sum, current_sum)

    # right of mid
    right_sum = float('inf')
    current_sum = 0
    for i in range(mid + 1, right + 1):
        current_sum += arr[i]
        right_sum = max(right_sum, current_sum)

    # sum of elements on the left and right of mid, which is the maximum sum that crosses the midpoint
    return left_sum + right_sum

def max_subarray_divide_and_conquer(arr, left, right):
    # base case: only one element
    if left == right:
        return arr[left]

    # find the midpoint
    mid = (left + right) // 2

    # recursively find the maximum subarray sum for the left and right halves
    left_sum = max_subarray_divide_and_conquer(arr, left, mid)
    right_sum = max_subarray_divide_and_conquer(arr, mid + 1, right)
    cross_sum = max_crossing_sum(arr, left, mid, right)

    # return the maximum of the three possible cases
    return max(left_sum, right_sum, cross_sum)

def max_subarray(arr):
    return max_subarray_divide_and_conquer(arr, 0, len(arr) - 1)


print(max_subarray([-2, -3, 4, -1, -2, 1, 5, -3]), "== 7")

Ini mengurangkan kerumitan masa kepada masa O(nlogn) kerana mula-mula tatasusunan dibahagikan kepada dua bahagian (O(logn)) dan kemudian mencari subarray lintasan maks mengambil masa O(n)

Algoritma Kadane: Penyelesaian O(n) yang Elegan

Ahli perangkawan Jay Kadane melihat kod itu dan segera mengenal pasti bahawa penyelesaian Shamos gagal menggunakan sekatan ketersambungan sebagai sebahagian daripada penyelesaian.

Inilah yang dia sedar

-Jika tatasusunan hanya mempunyai nombor negatif, maka jawapannya akan sentiasa menjadi nombor tunggal terbesar dalam tatasusunan, dengan mengandaikan kami tidak membenarkan subarray kosong.

-Jika tatasusunan hanya mempunyai nombor positif, jawapannya akan sentiasa menjumlahkan keseluruhan tatasusunan.

-Jika anda mempunyai tatasusunan nombor positif dan negatif, maka anda boleh melintasi tatasusunan langkah demi langkah. Jika pada bila-bila masa nombor yang anda lihat adalah lebih besar daripada jumlah semua nombor yang datang sebelum itu, penyelesaiannya tidak boleh memasukkan mana-mana nombor sebelumnya. Oleh itu, anda memulakan jumlah baharu daripada nombor semasa, sambil menjejaki jumlah maksimum yang ditemui setakat ini.

maxSubArray(nums):
    # avoiding type errors or index out of bounds errors
    if nums is None or len(nums) == 0:
        return 0


    max_sum = nums[0]  # max sum can't be smaller than any given element
    curr_sum = 0

    # Kadane's algorithm
    for num in nums:
        curr_sum = max(num, curr_sum + num)
        max_sum = max(curr_sum, max_sum)
    return max_sum

Apa yang saya suka tentang algoritma ini ialah ia boleh digunakan untuk banyak masalah lain. Cuba sesuaikan untuk menyelesaikan masalah LeetCode ini:

Satu dan Sifar
Subarray Pekeliling Jumlah Maksimum
Jumlah Subarray Saiz Minimum
Jumlah Subarray Menaik Maksimum
Subarray Produk Maksimum
Jumlah Subarray Berterusan
Jumlah Subarray Bergantian Maksimum (premium)
Jumlah Maks Segiempat Tidak Lebih Besar Daripada K

Atas ialah kandungan terperinci masalah subarray maks dan algoritma kadane. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!