Program Java untuk mengalih keluar pendua daripada timbunan tertentu

Dalam artikel ini, kami akan meneroka dua kaedah untuk mengalih keluar elemen pendua daripada timbunan di Java. Kami akan membandingkan pendekatan mudah dengan gelung bersarang dan kaedah yang lebih cekap menggunakan HashSet. Matlamatnya ialah untuk menunjukkan cara mengoptimumkan penyingkiran pendua dan menilai prestasi setiap pendekatan.

Pernyataan masalah

Tulis atur cara Java untuk mengalih keluar elemen pendua daripada timbunan.

Input

Stack<Integer> data = initData(10L);

Output

Unique elements using Naive Approach: [1, 4, 3, 2, 8, 7, 5]
Time spent for Naive Approach: 18200 nanoseconds

Unique elements using Optimized Approach: [1, 4, 3, 2, 8, 7, 5]
Time spent for Optimized Approach: 34800 nanoseconds

Untuk mengalih keluar pendua daripada timbunan tertentu, kami mempunyai 2 pendekatan −

• Pendekatan naif: Cipta dua gelung bersarang untuk melihat elemen yang sudah ada dan menghalangnya daripada menambahkannya pada pulangan timbunan hasil.
• Pendekatan HashSet: Gunakan Set untuk menyimpan elemen unik, dan manfaatkan kerumitan O(1)nya untuk menyemak sama ada elemen ada atau tidak.

Menjana dan mengklon tindanan rawak

Di bawah ialah program Java mula-mula membina tindanan rawak dan kemudian mencipta pendua untuk kegunaan selanjutnya −

private static Stack initData(Long size) {
    Stack stack = new Stack < > ();
    Random random = new Random();
    int bound = (int) Math.ceil(size * 0.75);
    for (int i = 0; i < size; ++i) {
        stack.add(random.nextInt(bound) + 1);
    }
    return stack;
}

private static Stack < Integer > manualCloneStack(Stack < Integer > stack) {
    Stack < Integer > newStack = new Stack < > ();
    for (Integer item: stack) {
        newStack.push(item);
    }
    return newStack;
}

initData membantu mencipta Tindanan dengan saiz yang ditentukan dan unsur rawak antara 1 hingga 100.

manualCloneStack membantu menjana data dengan menyalin data daripada tindanan lain, menggunakannya untuk perbandingan prestasi antara kedua-dua idea.

Alih keluar pendua daripada timbunan tertentu menggunakan pendekatan Naïve

Berikut ialah langkah untuk mengalih keluar pendua daripada timbunan tertentu menggunakan pendekatan Naïve −

• Mulakan pemasa.
• Buat tindanan kosong untuk menyimpan elemen unik.
• Lelaran menggunakan gelung while dan teruskan sehingga tindanan asal kosong, pop elemen atas.
• Semak pendua menggunakan resultStack.contains(element) untuk melihat sama ada elemen itu sudah ada dalam tindanan hasil.
• Jika elemen tiada dalam tindanan hasil, tambahkannya pada resultStack.
• Rekod masa tamat dan hitung jumlah masa yang dihabiskan.
• Pulangan hasil

Contoh

Di bawah ialah program Java untuk mengalih keluar pendua daripada timbunan tertentu menggunakan pendekatan Naïve −

public static Stack idea1(Stack stack) {
  long start = System.nanoTime();
  Stack resultStack = new Stack < > ();

  while (!stack.isEmpty()) {
    int element = stack.pop();
    if (!resultStack.contains(element)) {
      resultStack.add(element);
    }
  }
  System.out.println("Time spent for idea1 is %d nanosecond".formatted(System.nanoTime() - start));
  return resultStack;
}

Untuk pendekatan Naif, kami menggunakan

<code>while (!stack.isEmpty())</code>

untuk mengendalikan gelung pertama untuk melalui semua elemen dalam tindanan, dan gelung kedua ialah <div class="code" style="position:relative; padding:0px; margin:0px;"><pre class="brush:php;toolbar:false">resultStack.contains(element)</pre><div class="contentsignin">Salin selepas log masuk</div></div> untuk menyemak sama ada elemen itu sudah ada.

Alih keluar pendua daripada tindanan tertentu menggunakan pendekatan yang dioptimumkan (HashSet)

Berikut ialah langkah untuk mengalih keluar pendua daripada timbunan tertentu menggunakan pendekatan yang dioptimumkan −

• Mulakan pemasa
• Buat Set untuk menjejak elemen yang dilihat (untuk semakan kerumitan O(1).
• Buat timbunan sementara untuk menyimpan elemen unik.
• Lelaran menggunakan gelung sambil teruskan sehingga tindanan kosong .
• Alih keluar elemen atas daripada timbunan.
• Untuk menyemak pendua kami akan menggunakan dilihat.mengandungi(elemen) untuk menyemak sama ada elemen itu sudah ada dalam set.
• Jika elemen tiada dalam set, tambahkannya pada timbunan yang dilihat dan sementara.
• Rekod masa tamat dan hitung jumlah masa yang dihabiskan.
• Kembalikan hasilnya

Contoh

Di bawah ialah program Java untuk mengalih keluar pendua daripada timbunan tertentu menggunakan HashSet −

public static Stack<Integer> idea2(Stack<Integer> stack) {
    long start = System.nanoTime();
    Set<Integer> seen = new HashSet<>();
    Stack<Integer> tempStack = new Stack<>();

    while (!stack.isEmpty()) {
        int element = stack.pop();
        if (!seen.contains(element)) {
            seen.add(element);
            tempStack.push(element);
        }
    }
    System.out.println("Time spent for idea2 is %d nanosecond".formatted(System.nanoTime() - start));
    return tempStack;
}

Untuk pendekatan yang dioptimumkan, kami menggunakan

<code>Set<Integer> seen</code>

to menyimpan elemen unik dalam Set, manfaatkan O(1) kerumitan apabila mengakses elemen rawak untuk mengurangkan kos pengiraan untuk menyemak sama ada elemen ada atau tidak.

Menggunakan kedua-dua pendekatan bersama

Di bawah ialah langkah untuk mengalih keluar pendua daripada timbunan tertentu menggunakan kedua-dua pendekatan yang disebutkan di atas -

• Memulakan data yang kami gunakan kaedah initData(Saiz panjang) untuk mencipta tindanan yang diisi dengan integer rawak.
  
• Klon Tindanan yang kita gunakan kaedah cloneStack(Timbunan) untuk mencipta salinan tepat tindanan asal.
Jana tindanan awal dengan
• initData.
Klon tindanan ini menggunakan
• cloneStack.
Gunakan
•  pendekatan naif untuk mengalih keluar pendua daripada timbunan asal.
Gunakan
• pendekatan dioptimumkan untuk mengalih keluar pendua daripada timbunan klon.
Paparkan masa yang diambil untuk setiap kaedah dan elemen unik yang dihasilkan oleh kedua-dua pendekatan

Contoh 

Di bawah ialah program Java yang mengalih keluar elemen pendua daripada timbunan menggunakan kedua-dua pendekatan yang dinyatakan di atas −

import java.util.HashSet;
import java.util.Random;
import java.util.Set;
import java.util.Stack;

public class DuplicateStackElements {
    private static Stack<Integer> initData(Long size) {
        Stack<Integer> stack = new Stack<>();
        Random random = new Random();
        int bound = (int) Math.ceil(size * 0.75);
        for (int i = 0; i < size; ++i) {
            stack.add(random.nextInt(bound) + 1);
        }
        return stack;
    }
    private static Stack<Integer> cloneStack(Stack<Integer> stack) {
        Stack<Integer> newStack = new Stack<>();
        newStack.addAll(stack);
        return newStack;
    }
    public static Stack<Integer> idea1(Stack<Integer> stack) {
        long start = System.nanoTime();
        Stack<Integer> resultStack = new Stack<>();

        while (!stack.isEmpty()) {
            int element = stack.pop();
            if (!resultStack.contains(element)) {
                resultStack.add(element);
            }
        }
        System.out.printf("Time spent for idea1 is %d nanoseconds%n", System.nanoTime() - start);
        return resultStack;
    }
    public static Stack<Integer> idea2(Stack<Integer> stack) {
        long start = System.nanoTime();
        Set<Integer> seen = new HashSet<>();
        Stack<Integer> tempStack = new Stack<>();

        while (!stack.isEmpty()) {
            int element = stack.pop();
            if (!seen.contains(element)) {
                seen.add(element);
                tempStack.push(element);
            }
        }
        System.out.printf("Time spent for idea2 is %d nanoseconds%n", System.nanoTime() - start);
        return tempStack;
    }
    public static void main(String[] args) {
        Stack<Integer> data1 = initData(10L);
        Stack<Integer> data2 = cloneStack(data1);
        System.out.println("Unique elements using idea1: " + idea1(data1));
        System.out.println("Unique elements using idea2: " + idea2(data2));
    }
}

Output

Perbandingan

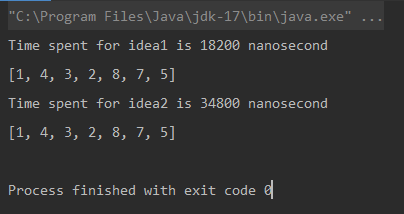
* Unit ukuran ialah nanosaat.

public static void main(String[] args) {
    Stack<Integer> data1 = initData(<number of stack size want to test>);
    Stack<Integer> data2 = manualCloneStack(data1);
    idea1(data1);
    idea2(data2);
}

Method	100 elements	1000 elements	10000 elements	100000 elements	1000000 elements
Idea 1	693100	4051600	19026900	114201800	1157256000
Idea 2	135800	681400	2717800	11489400	36456100

As observed, the time running for Idea 2 is shorter than for Idea 1 because the complexity of Idea 1 is O(n²), while the complexity of Idea 2 is O(n). So, when the number of stacks increases, the time spent on calculations also increases based on it.

---

Atas ialah kandungan terperinci Program Java untuk mengalih keluar pendua daripada timbunan tertentu. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!