
Untuk mengisih maklumat dalam susunan tertentu, selalunya dalam rangka kerja seperti tatasusunan, ialah menyusunnya. Anda boleh menggunakan keperluan urutan yang berbeza; yang popular ialah mengisih nombor daripada terkecil kepada terbesar atau sebaliknya, atau rentetan pengisihan secara leksikografi. Kami akan merangkumi algoritma yang berbeza, daripada alternatif yang tidak berkesan tetapi intuitif hingga kepada algoritma yang cekap yang dilaksanakan dengan berkesan dalam Java dan dalam bahasa lain jika anda berminat dengan cara pengisihan berfungsi.
Terdapat algoritma pengisihan yang berbeza, dan tidak semuanya sama berkesan. Untuk membandingkannya dan melihat mana yang berprestasi terbaik, kami akan menganalisis kerumitan masanya.
IKLAN Kursus Popular dalam kategori ini JAVA MASTERY - Pengkhususan | 78 Siri Kursus | 15 Ujian Olok-olokKonsep di sebalik Insertion Sort membahagikan julat kepada sub-baris yang diisih dan tidak diisih. Bahagian terperingkat adalah pada permulaan tempoh 1 dan sepadan dengan komponen pertama (sebelah kiri) dalam tatasusunan. Kami bergerak melalui tatasusunan dan mengembangkan bahagian terperingkat tatasusunan dengan satu komponen semasa setiap lelaran. Apabila kami mengembangkan, kami meletakkan elemen baharu dalam sub-tatasusunan yang diisih. Kami melakukan ini dengan mengalihkan semua elemen ke kanan sehingga kami mendapati bahawa kami tidak perlu menukar komponen pertama. Apabila bahagian tebal diisih dalam tertib menaik, contohnya, dalam tatasusunan berikut, ia berlaku:
Kod:
public class InsertionSortEx {
public static void insertionSort(int[] arr) {
for (int x = 1; x < arr.length; x++) {
int current = arr[x];
int y = x - 1;
while(y >= 0 && current < arr[y]) {
arr[y+1] = arr[y];
y--;
}
arr[y+1] = current;
}
}
public static void main(String a[]){
int[] arr1 = {3,5,7,8,4,2,1,9,6};
System.out.println("Before Sorting");
for(int x:arr1){
System.out.print(x+" ");
}
System.out.println();
insertionSort(arr1);//sorting array using insertion sort
System.out.println("After Insertion Sorting");
for(int x:arr1){
System.out.print(x+" ");
}
}
}Output:
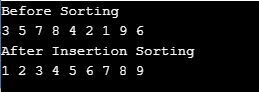
Mengikut kaedah ini, satu komponen memanjangkan bahagian yang diisih; kita kini mempunyai lima bukannya empat elemen. Setiap lelaran melakukan ini, dan keseluruhan tatasusunan akan diisih pada penghujungnya.
Nota: Ini kerana kita perlu memindahkan keseluruhan senarai terperingkat satu demi satu dalam setiap lelaran, iaitu O(n). Kita mesti melakukan ini untuk setiap komponen dalam setiap jadual, yang membayangkan bahawa ia adalah sempadan O(n^2).2.Jika gelembung tidak dalam susunan yang diperlukan, ia beroperasi dengan menggantikan komponen yang berdekatan. Ini diulang sehingga semua komponen teratur dari permulaan tatasusunan. Kami tahu bahawa jika kami berjaya melakukan keseluruhan lelaran tanpa swap, semua item berbanding dengan elemen bersebelahan mereka berada dalam susunan yang diingini dan, dengan lanjutan, keseluruhan tatasusunan. Sebab untuk algoritma Isih Buih ialah nombor seperti "buih naik" ke dalam "tanah". Jika, selepas amaun tertentu, anda melalui contoh itu sekali lagi (4 adalah contoh yang baik), anda akan perasan bahawa nombor itu perlahan-lahan bergerak ke kanan.
Langkah-langkah untuk Isih Buih adalah seperti berikut:
Kod:
public class BubbleSortExample {
public static void bubbleSort(int[] arr) {
int n = arr.length;
int tmp = 0;
for(int x=0; x < n; x++){
for(int y=1; y < (n-x); y++){
if(arr[y-1] > arr[y]){
//swap elements
tmp = arr[y-1];
arr[y-1] = arr[y];
arr[y] = tmp;
}
}
}
}
public static void main(String[] args) {
int arr[] ={4,2,1,5,3};
System.out.println("Array Before Bubble Sort");
for(int x=0; x < arr.length; x++){
System.out.print(arr[x] + " ");
}
System.out.println();
bubbleSort(arr);
System.out.println("Array After Bubble Sort");
for(int x=0; x < arr.length; x++){
System.out.print(arr[x] + " ");
}
}
}Output:
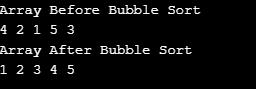
Isih Pilihan membahagi tatasusunan kepada tatasusunan klasifikasi yang tidak diisih. Kali ini, walau bagaimanapun, subbaris pengisihan dibentuk dengan memasukkan pada penghujung tatasusunan yang diisih elemen minimum subbaris yang tidak diisih dengan menukar:
Kod:
public class SelectionSortEx {
public static void selectionSort(int[] arr){
for (int x = 0; x < arr.length - 1; x++)
{
int indx = x;
for (int y = x + 1; y < arr.length; y++){
if (arr[y] < arr[indx]){
indx = y;
}
}
int smallNumber = arr[indx];
arr[indx] = arr[x];
arr[x] = smallNumber;
}
}
public static void main(String a[]){
int[] arr1 = {3,5,1,2,4};
System.out.println("Before Sorting");
for(int x:arr1){
System.out.print(x+" ");
}
System.out.println();
selectionSort(arr1);
System.out.println("After Selection Sorting");
for(int x:arr1){
System.out.print(x+" ");
}
}
}Output:
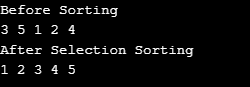
Merge Sort utilizes recursion to fix the issue of the divide and conquest method more effectively than earlier described algorithms.
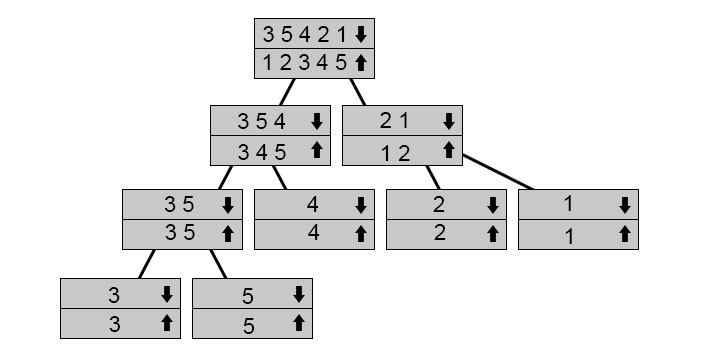
This tree shows how the recursive calls function. Down arrow marked arrays are the arrays for which we call function while we fuse up arrow arrays. Then you follow the arrow to the tree’s edge and then return and merge. We’ve got 3 5 3 1 range, so we split it into 3 5 4 and 2 1. We split them into their parts in order to sort them. We begin fusioning and sorting them as we go when we get to the bottom.
Code:
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
public class MergeSort {
static void merge(int[] array,int lowval,int midval,int highval){
int x, y ,k;
int[] c= new int[highval-lowval+1];
k = 0;
x=lowval;
y=midval+1;
while(x<=midval && y<=highval){
if(array[x]<=array[y]){
c[k++] = array[x++];
}
else{
c[k++] = array[y++];
}
}
while(x<=midval){
c[k++] = array[x++];
}
while(y<=highval){
c[k++] = array[y++];
}
k=0;
for(x = lowval; x<=highval; x++){
array[x] = c[k++];
}
}
static void mergeSort(int[] array,int lowval, int highval){
if(highval-lowval+1>1){
int midval = (lowval+highval)/2;
mergeSort(array,lowval,midval);
mergeSort(array,midval+1,highval);
merge(array,lowval,midval,highval);
}
}
public static void main(String[] args) {
BufferedReader r = new BufferedReader(new InputStreamReader(System.in));
int size;
System.out.println("Enter the array");
try {
size = Integer.parseInt(r.readLine());
} catch (Exception e) {
System.out.println("Please Enter valid Input");
return;
}
int[] array = new int[size];
System.out.println("Enter array elements");
int x;
for (x = 0; x < array.length; x++) {
try {
array[x] = Integer.parseInt(r.readLine());
} catch (Exception e) {
System.out.println("An error Occurred");
}
}
System.out.println("After Sorting");
System.out.println(Arrays.toString(array));
mergeSort(array,0,array.length-1);
System.out.println("Before Merge Sorting");
System.out.println(Arrays.toString(array));
}
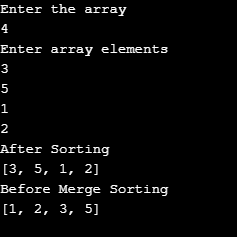
}In this program, we have asked the user to enter input. The output will be in sorted order based on the user’s input.
Output:
You first must know the framework on which Heapsort operates-the heap-in order to comprehend why it operates. We will specifically speak about a binary heap, but you can also generalize this to other heap constructions. A heap is a tree that fulfills the property of the heap, namely that all its kids have relationships to each node. A heap must also be nearly finished. A near-complete d-depth binary has a d-1 subtree with the same root, and each node has a full, left subtree, with a left descending.
In other words, you get a lower and lower number (min-heap) or larger and bigger (max-heap) when moving down the tree. Here is a max-heap instance:
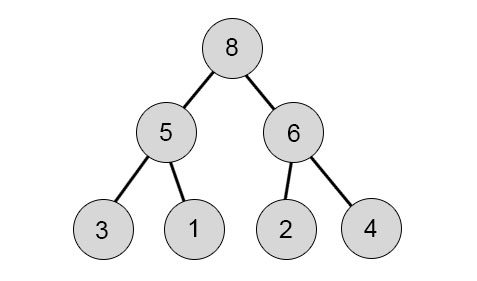
After Repeating this process again, we will get the following results:
Code:
public class HeapSort
{
public void sort(int arr[])
{
int n = arr.length;
for (int x = n / 2 - 1; x >= 0; x--)
heapify(arr, n, x);
for (int x=n-1; x>=0; x--)
int tmp = arr[0];
arr[0] = arr[x];
arr[x] = tmp;
heapify(arr, x, 0);
}
}
void heapify(int arr[], int n, int x)
{
int largest = x;
int L = 2*x + 1;
int r = 2*x + 2;
if (L < n && arr[L] > arr[largest])
largest = L;
if (r < n && arr[r] > arr[largest])
largest = r;
if (largest != x)
{
int swap = arr[x];
arr[x] = arr[largest];
arr[largest] = swap;
heapify(arr, n, largest);
}
}
static void printArray(int arr[])
{
int n = arr.length;
for (int x=0; x<n; ++x)
System.out.print(arr[x]+" ");
System.out.println();
}
public static void main(String args[])
{
int arr[] = {6,1,8,3,5,2,4};
int n = arr.length;
System.out.println("Before Sorting:");
printArray(arr);
HeapSort ob = new HeapSort();
ob.sort(arr);
System.out.println("After Heap Sorting:");
printArray(arr);
}
}Output:
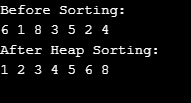
You can view it from point to level of the graph, from left to right. We achieved here that when we have the kth component in the array, the position of its children is 2\*k+1 and 2\*k+2 (assuming that indexing begins at 0). You can monitor this. The position of the parent is always (k-1)/2 for the kth component. You can readily “max heap up” any range because you know that. Check whether one of its kids is lower than that for each component. If so, pair one parent and repeat this step recursively with the parent.
Note: Since iterating for-loops across the entire array makes heapSort) (obviously O(N), it would create Heapsort O’s overall complexity(nlog n). Heapsort has an on-the-spot type, which means that it requires O(1) more room than Merge Sort, but it has some disadvantages, such as parallels that are hard.Sorting is a very prevalent procedure with datasets, whether for further analysis, speeding search with more effective algorithms relying on sorted information, filtering information, etc. Several languages endorse sorting, and often the interfaces obscure what the programmer does.
Atas ialah kandungan terperinci Mengisih Algoritma dalam Java. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!




