
Dalam artikel Patterns in Java, sebelum mempelajari mana-mana bahasa pengaturcaraan dalam Java dan mendalami konsep lanjutan, adalah penting untuk memahami cara kerja gelung. Walaupun terdapat 3 jenis gelung iaitu gelung for, while dan do-while. Setiap gelung digunakan mengikut situasi tertentu program kerana ia berbeza sedikit antara satu sama lain. Untuk menggunakan pelbagai gelung memerlukan beberapa logik pengaturcaraan, dan untuk tujuan ini, amalan corak diberikan kepada pengaturcara kerana ia melibatkan penggunaan kuasa logik dan penaakulan. Contohnya, ia boleh mencetak angka geometri (seperti segi tiga, segi empat sama, dsb.), piramid, kotak dalam pelbagai corak bintang, nombor dan gaya watak pada skrin konsol. Format atau sintaks asas gelung mungkin berbeza dari satu bahasa pengaturcaraan ke bahasa lain, tetapi logik umum untuk mencetak corak ini tetap sama.
IKLAN Kursus Popular dalam kategori ini JAVA MASTERY - Pengkhususan | 78 Siri Kursus | 15 Ujian Olok-olokMari kita fahami cara melukis corak dalam Java melalui beberapa contoh
Kod:
public class Pyramid
{
public static void main(String[] args)
{
int i, j;
//outermost loop to represent the number of rows which is 5 in this case for(i= 1; i<= 5; i++)
{
//innermost loop is to print the numbers in the specific rows for (j=1; j<=i; j++)
{
System.out.print(j +" " );
}
System.out.println();
}
}
}Output:

Dalam contoh di atas, hanya 2 gelung asas diperlukan untuk mencetak corak; yang pertama untuk gelung adalah untuk bilangan baris. Dalam kes kami, kami telah menentukan baris, iaitu 5, jika tidak, kami juga boleh mengambil input daripada pengguna dan menyimpannya dalam pembolehubah. Gelung dalam adalah untuk mencetak nombor dalam baris tertentu; Selepas selesai 1 baris atau penghujung gelung 'j', baris ditukar menggunakan println().
Kod:
public class NumberTriangle
{
public static void main(String[] args)
{
int i, j;
int rows =7;
//outermost loop to represent the number of rows which is 7 in this case
//for the upper half of arrow
for (i=1; i<= rows; i++)
{
//innermost loop is to print the numbers in the specific rows
//for the upper half of arrow
for (j=1; j<=i; j++)
{
System.out.print(j + " ");
}
System.out.println();
}
//outermost loop to represent the number of rows which is 6 in this case
//for the lower half of arrow
for (i=rows-1; i>=1; i--)
{
//innermost loop is to print the numbers in the specific rows
//for the lower half of arrow
for (j=1; j<=i; j++)
{
System.out.print(j + " ");
}
System.out.println();
}
}
}Output:
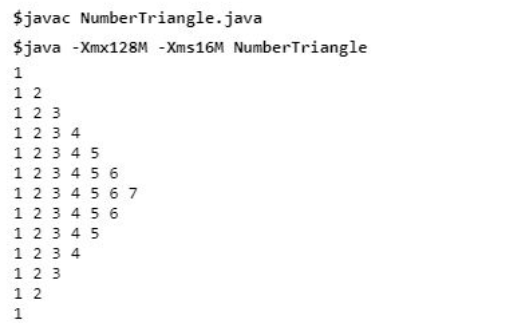
Dalam contoh di atas, kita perlu membahagikan anak panah kepada dua bahagian dan menggunakan 2 gelung untuk setiap separuh. Separuh pertama baris ialah nilai awal yang ditetapkan untuk baris, manakala kiraan baris adalah 1 kurang daripada nilai awal untuk bahagian bawah. Gelung dalam untuk kedua-dua bahagian digunakan untuk melelaran melalui setiap baris mengikut gelung luar.
Kod:
public class FullPyramid
{
public static void main(String[] args)
{
int i, j, k;
int rows = 5;
//outermost loop to represent the number of rows which is 5 in this case for(i= 1; i<= rows; i++)
{
//innermost loop to represent the spaces in pyramid for (j= 1; j<= rows-i; j++)
{
System.out.print(" ");
}
//innermost loop to represent the stars (*) in pyramid for (k= 1; k<= 2*i-1; k++)
{
System.out.print("* ");
}
System.out.println();
}
}
}Output:
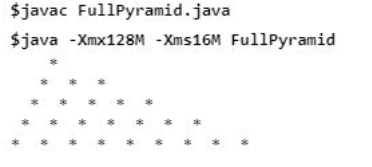
Dalam contoh di atas, kita perlu melakukan 3 perkara, iaitu mengingati jumlah bilangan baris untuk pencetakan piramid yang mana gelung pertama untuk berfungsi daripada pembolehubah 1 kepada baris. Kedua, kita perlu mencetak ruang dalam piramid dahulu dan kemudian corak (*) selepas ruang. Untuk kedua dan ketiga ini, untuk gelung digunakan di dalam gelung luar ‘i’.
Kod:
public class ReversePyramid
{
public static void main(String[] args)
{
int i, j, k;
int rows = 5;
//outermost loop to represent the number of rows which is 5 in this case for(i= 1; i<= rows; i++)
{
//innermost loop to represent the spaces
for (j= 1; j<= rows-1; j++)
{
System.out.print(" ");
}
//innermost loop to represent the stars (*) in pyramid for (k= 1; k<= i; k++)
{
System.out.print("* ");
}
System.out.println();
}
}
}Output:
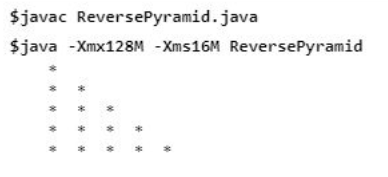
Separuh piramid mudah adalah mudah kerana kita perlu mengendalikan nombor, * atau aksara yang kita cetak, tetapi untuk piramid terbalik, kita perlu mencetak dahulu ruang dan kemudian corak, iaitu (*) dalam kes kita . Jadi 3 untuk gelung digunakan, berfungsi sama dengan gelung dalam kes piramid penuh.
Kod:
public class AlphabetPyramid
{
public static void main(String[] args)
{
int i, j;
//outermost loop to represent the number of rows which is 5 in this case for(i= 1; i<= 5; i++)
{
int ch = 65;
//innermost loop to represent the alphabets in a pyramid in particular row for (j= 1; j<= i; j++)
{
System.out.print((char)(ch + i - 1) + " ");
}
System.out.println();
}
}
}Output:
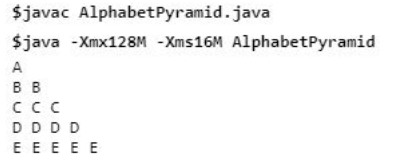
Piramid dicetak dengan logik yang sama seperti yang digunakan dalam contoh di atas, menggunakan 2 untuk gelung, satu untuk bilangan baris dan lain-lain untuk mencetak aksara dalam baris tertentu. Tetapi perkara utama yang perlu diberi perhatian ialah pengendalian data aksara. Contohnya, ‘A’ mempunyai nilai berangka 65 dalam Java, jadi semua logik matematik dilakukan menggunakan nilai berangka abjad, dan pada akhirnya, ia dicetak dalam format aksara.
Kod:
public class AlphabetPattern
{
public static void main(String[] args)
{
int i, j;
//outermost loop to represent the number of rows which is 5 in this case for(i= 1; i<= 5; i++)
{
int ch = 65;
//innermost loop to represent the alphabets for (j= 1; j<= i; j++)
{
System.out.print((char)(ch - 1 + j) + " ");
}
System.out.println();
}
}
}Output:

Corak asas yang diikuti untuk menangani nilai aksara dan 2 untuk gelung dalam contoh di atas adalah serupa dengan Contoh 5 cuma perbezaan ialah logik mudah yang digunakan untuk mencetak corak yang diingini.
Kod:
public class SquarePattern
{
public static void main(String[] args)
{
int i, j;
//outermost loop to represent the number of rows which is 5 in this case for(i= 1; i<= 5; i++)
{
int ch = 65;
//innermost loop to represent the stars (*) for (j= 1; j<= 5; j++)
{
System.out.print(" * " + " ");
}
System.out.println();
}
}
}Output:

For printing of square, we need length and width, i.e. both sides of the square should be the same, which is 5 in our case. So the first loop is used for the length or number of rows in the square, and the inner loop is used for the width of the square, i.e. 5 stars in a single row.
Code:
public class RectanglePattern
{
public static void main(String[] args)
{
int i, j;
//outermost loop to represent the number of rows which is 5 in this case for(i= 1; i<= 5; i++)
{
int ch = 65;
//innermost loop to represent columns the stars (*) for (j= 1; j<= 9; j++)
{
System.out.print(" * " + " " );
}
System.out.println();
}
}
}Output:

The basic logic of printing the rectangle of (*) is the same as printing of squares, the only difference between is the different length and width of the rectangle. Here ‘i’ loop is for the length of the rectangle, and the inner ‘j’ loop is for the width of the loop. Our program is taken as a constant value; we can also ask the user and store them in separate variables.
Printing a diamond in Java is a very simple process. It involves printing 2 pyramids, 1 in the upward direction and another in an inverted direction. Basically, we need to use the loops to do the coding to print two separate pyramids.
Code:
public class Diamond
{
public static void main(String[] args)
{
int i, j, k;
int rows = 5;
//outermost loop to represent the number of rows which is 5 in this case.
// Creating upper pyramid
for(i= 1; i<= rows; i++)
{
//innermost loop to represent the spaces in upper pyramid for (j= 1; j<= rows-i; j++)
{
System.out.print(" ");
}
//innermost loop to represent the stars (*) in upper pyramid for (k= 1; k<= 2*i-1; k++)
{
System.out.print("* ");
}
System.out.println();
}
//outermost loop for the rows in the inverted pyramid for (i = rows-1; i>0; i--)
{
//innermost loop for the space present in the inverted pyramid for (j=1; j<= rows - i; j++)
{
System.out.print(" ");
}
//innermost loop inside the outer loop to print the ( * ) pattern in inverted pyramid for (k = 1; k<= 2*i-1; k++)
{
System.out.print("* ");
}
System.out.println();
}
}
}In the above example, almost the same logic is applied to create both pyramids, one in an upward direction and another in an inverted direction. Thus, the first loop is for the number of lines or rows in the pattern, and the second is for spaces and the stars (*) pattern in the pattern.
Output:

Code:
public class BinaryStair
{
public static void main(String[] args)
{
int i, j;
//outer loop for the total rows which is 5 in this case for (i = 1; i <= 5; i++)
{
//inner loop for the pattern of 0 and 1 in each row for (j = 1; j<= i ; j++)
{
if (j % 2 ==0)
{
System.out.print(0);
}
else
{
System.out.print(1);
}
}
System.out.println();
}
}
}Output:
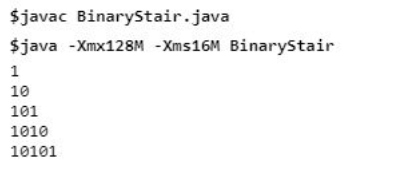
In the above example, in order to print binary pattern, outer for loop ‘i’ is used for a total number of rows, and the inner for loop ‘j’ is used to iterate till the outer loop ‘i’ because for the 1st row, we need 1 value, for the 2nd row we need 2 values, and so on. If and else statements are used in order to print the alternate value of 0 and 1. Suppose for the first time i=1, j=1 and 1%2 != 0, then 1 is printed, and execution will move out of the inner loop.
Code:
public class AlphabetReverseOrder
{
public static void main(String[] args)
{
int i, j, k;
//outer loop for the total rows which is 5 in this case for (i = 0 ; i<=5; i++)
{
int ch= 65;
//inner loop for the pattern of alphabets in till ‘i’ loop for (j = 0; j <=i ; j++)
{
System.out.print((char) (ch+j) + " ");
}
//inner loop for the pattern of alphabets in reverse order from ‘i’ loop for (k= i-1; k >=0; k--)
{
System.out.print((char) (ch+k) + " ");
}
System.out.println();
}
}
}Output:

In the above example, if we observe each row of pattern, we need to print the alphabet first in the increasing order, i.e. A B and then in the reverse order, i.e. A B A. For this, we need 3 loops, 1st for loop for the total number of rows. 2nd for loop to print the alphabets in increasing order then the 3rd for loop which remains inside the outer ‘i’ loop and prints the alphabets in the same line but in reverse order of ‘j’ loop.
The above example and their explanations clearly show how to make such patterns in Java. Though these patterns seem to be difficult in the starting, observing them deeply of how the repetition of pattern is happening in a single row and according to how many loops should be used, it becomes easy to do hands-on on this. Today also, in interviews of big companies, candidates are asked to write the logic of patterns of varying difficulty levels because this pattern making shows the basic logical and programming knowledge of an individual.
Atas ialah kandungan terperinci Corak di Jawa. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!




