Ubah suai Pemberat Tepi Graf

2699. Ubah suai Pemberat Tepi Graf

Kesukaran: Sukar

Topik: Graf, Timbunan (Baris Gilir Keutamaan), Laluan Terpendek

Anda diberi graf berwajaran tidak terarah disambungkan yang mengandungi n nod berlabel dari 0 hingga n - 1 dan tepi tatasusunan integer dengan tepi[i] = [a_i, b _i, w_i] menunjukkan bahawa terdapat tepi antara nod a_i dan b_i dengan berat w_i.

Sesetengah sisi mempunyai berat -1 (w_i = -1), manakala yang lain mempunyai berat positif (w_i > 0) .

Tugas anda ialah mengubah suai semua tepi dengan berat -1 dengan memberikannya nilai integer positif dalam julat [1, 2 * 10⁹ ] supaya jarak terpendek antara sumber nod dan destinasi menjadi sama dengan sasaran integer. Jika terdapat pelbagai pengubahsuaian yang menjadikan jarak terpendek antara sumber dan destinasi sama dengan sasaran, mana-mana daripadanya akan dianggap betul.

Kembalikan tatasusunan yang mengandungi semua tepi (walaupun yang tidak diubah suai) dalam sebarang susunan jika mungkin untuk menjadikan jarak terpendek dari sumber ke destinasi sama dengan sasaran, atau tatasusunan kosong jika mustahil .

Nota: Anda tidak dibenarkan mengubah suai pemberat tepi dengan pemberat positif awal.

Contoh 1:

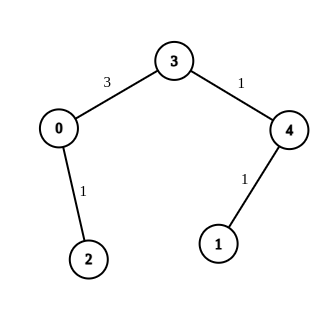
• Input: n = 5, tepi = [[4,1,-1],[2,0,-1],[0,3,-1],[4,3,-1] ], sumber = 0, destinasi = 1, sasaran = 5
• Output: [[4,1,1],[2,0,1],[0,3,3],[4,3,1]]
• Penjelasan: Graf di atas menunjukkan kemungkinan pengubahsuaian pada tepi, menjadikan jarak dari 0 hingga 1 sama dengan 5.

Contoh 2:

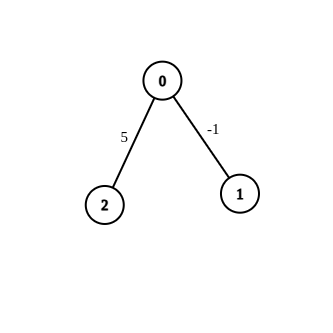
• Input: n = 3, tepi = [[0,1,-1],[0,2,5]], sumber = 0, destinasi = 2, sasaran = 6
• Output: []
• Penjelasan: Graf di atas mengandungi tepi awal. Tidak mungkin untuk membuat jarak dari 0 hingga 2 sama dengan 6 dengan mengubah suai tepi dengan berat -1. Jadi, tatasusunan kosong dikembalikan.

Contoh 3:

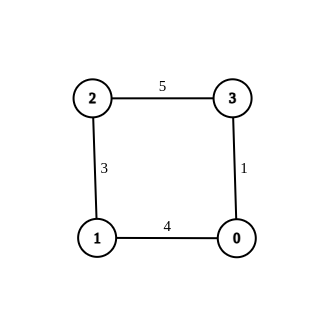
• Input: n = 4, tepi = [[1,0,4],[1,2,3],[2,3,5],[0,3,-1]], sumber = 0, destinasi = 2, sasaran = 6
• Output: [[1,0,4],[1,2,3],[2,3,5],[0,3,1]]
• Penjelasan: Graf di atas menunjukkan graf diubah suai yang mempunyai jarak terpendek dari 0 hingga 2 sebagai 6.

Kekangan:

• 1 <= n <= 100
• 1 <= tepi.panjang <= n * (n - 1) / 2
• tepi[i].panjang == 3
• 0 <= a_i, b_i < n
• w_i = -1 atau 1 <= w_i <= 10⁷
• a_i != b_i
• 0 <= sumber, destinasi < n
• sumber != destinasi
• 1 <= sasaran <= 10⁹
• Graf disambungkan dan tiada gelung kendiri atau tepi berulang

Petunjuk:

1. Pertama sekali, semak sama ada anda boleh membuat laluan terpendek dari sumber ke destinasi sama dengan sasaran.
2. Jika laluan terpendek dari sumber ke destinasi tanpa tepi untuk diubah suai, adalah kurang daripada sasaran, maka ia tidak boleh dilakukan.
3. Jika laluan terpendek dari sumber ke destinasi termasuk tepi yang akan diubah suai dan memberikan mereka berat sementara 1, adalah lebih besar daripada sasaran, maka ia juga tidak mungkin.
4. Andaikan kita boleh mencari tepi boleh diubah suai (u, v) supaya panjang laluan terpendek dari sumber ke u (dis1) ditambah panjang laluan terpendek dari v ke destinasi (dis2) adalah kurang daripada sasaran (dis1 + dis2 < target), maka kita boleh menukar beratnya kepada “target - dis1 - dis2”.
5. Untuk semua sisi lain yang masih mempunyai berat "-1", tukar pemberat kepada nombor besar yang mencukupi (sasaran, sasaran + 1 atau 200000000 dll.).

Penyelesaian:

Kita boleh memecahkan pendekatan seperti berikut:

Pendekatan:

1. Semakan Awal dengan Berat Sedia Ada:

   • Mula-mula, kami mengira laluan terpendek dari sumber ke destinasi menggunakan hanya tepi dengan pemberat positif, mengabaikan tepi dengan berat -1.
   • Jika jarak ini sudah lebih besar daripada sasaran, maka adalah mustahil untuk mengubah suai -1 tepi untuk mencapai sasaran, jadi kami mengembalikan tatasusunan kosong.

2. Tugas Sementara Berat 1:

   • Seterusnya, tetapkan berat sementara 1 pada semua tepi dengan berat -1 dan kira semula laluan terpendek.
   • Jika laluan terpendek ini masih lebih besar daripada sasaran, maka adalah mustahil untuk mencapai sasaran, jadi kami mengembalikan tatasusunan kosong.

3. Ubah suai Berat Tepi Tertentu:

   • Lelar melalui tepi dengan berat -1 dan kenal pasti tepi yang boleh dilaraskan agar sepadan dengan jarak sasaran. Ini dilakukan dengan melaraskan berat tepi supaya gabungan jarak laluan menuju dan dari tepi ini menghasilkan jarak sasaran yang tepat.
   • Untuk mana-mana baki -1 tepi, tetapkan berat yang cukup besar (cth., 2 * 10^9) untuk memastikan ia tidak menjejaskan laluan terpendek.

4. Kembalikan Tepi Ubah Suai:

   • Akhir sekali, kembalikan senarai tepi yang diubah suai.

Mari laksanakan penyelesaian ini dalam PHP: 2699. Ubah suai Pemberat Tepi Graf

  
  
  Penjelasan:



Fungsi dijkstra mengira laluan terpendek dari sumber ke semua nod lain.
Kami pada mulanya mengira laluan terpendek tanpa menghiraukan -1 tepi.
Jika laluan tanpa -1 tepi kurang daripada sasaran, fungsi mengembalikan tatasusunan kosong, menunjukkan mustahil untuk melaraskan pemberat untuk memenuhi sasaran.
Jika tidak, kami tetapkan semua -1 tepi kepada 1 buat sementara waktu dan semak sama ada laluan terpendek melebihi sasaran.
Jika ia berlaku, sekali lagi mustahil untuk mencapai sasaran, dan kami mengembalikan tatasusunan kosong.
Kami kemudian mengubah suai pemberat -1 tepi secara strategik untuk mencapai laluan terpendek yang diingini tepat sasaran.


Pendekatan ini memeriksa dan melaraskan pemberat tepi dengan cekap, memastikan jarak sasaran dipenuhi jika boleh.

Pautan Kenalan

Jika anda mendapati siri ini membantu, sila pertimbangkan untuk memberi repositori bintang di GitHub atau berkongsi siaran pada rangkaian sosial kegemaran anda ?. Sokongan anda amat bermakna bagi saya!

Jika anda mahukan kandungan yang lebih berguna seperti ini, sila ikuti saya:


LinkedIn
GitHub



          

            
  

            
        
Atas ialah kandungan terperinci Ubah suai Pemberat Tepi Graf. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!