
Tepi berwajaran boleh disimpan dalam senarai bersebelahan.
Terdapat dua jenis graf berwajaran: berwajaran puncak dan berwajaran tepi. Dalam graf berwajaran bucu, setiap bucu diberi pemberat. Dalam graf berwajaran tepi, setiap tepi diberi pemberat. Daripada kedua-dua jenis, graf berwajaran tepi mempunyai lebih banyak aplikasi. Bab ini mempertimbangkan graf berwajaran tepi.
Graf berwajaran boleh diwakili dengan cara yang sama seperti graf tidak berwajaran, kecuali anda perlu mewakili pemberat pada tepi. Seperti graf tidak berwajaran, bucu dalam graf berwajaran boleh disimpan dalam tatasusunan. Bahagian ini memperkenalkan tiga perwakilan untuk tepi dalam graf berwajaran.
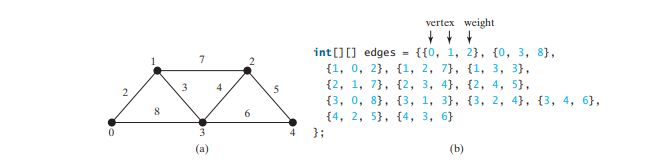
Tepi berwajaran boleh diwakili menggunakan tatasusunan dua dimensi. Sebagai contoh, anda boleh menyimpan semua tepi dalam graf dalam Rajah di bawah (a) menggunakan tatasusunan dalam Rajah di bawah (b).
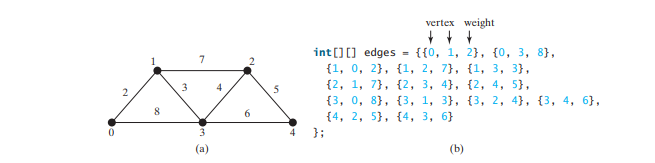
Berat boleh terdiri daripada sebarang jenis: Integer, Double, BigDecimal dan sebagainya. Anda boleh menggunakan tatasusunan dua dimensi daripada jenis Objek untuk mewakili tepi berwajaran seperti berikut:
Objek[][] tepi = {
{Integer baharu(0), Integer baharu(1), SomeTypeForWeight(2)} baharu,
{Integer baharu(0), Integer baharu(3), SomeTypeForWeight(8)} baharu,
...
};
Andaikan graf mempunyai n bucu. Anda boleh menggunakan matriks n * n dua dimensi, katakan berat, untuk mewakili pemberat pada tepi. berat[i][j] mewakili berat di tepi (i, j). Jika bucu i dan j tidak disambungkan, berat[i][j] ialah null. Sebagai contoh, pemberat dalam graf dalam Rajah di atas (a) boleh diwakili menggunakan matriks bersebelahan seperti berikut:

Cara lain untuk mewakili tepi ialah dengan mentakrifkan tepi sebagai objek. Kelas AbstractGraph.Edge ditakrifkan untuk mewakili kelebihan tidak berwajaran dalam AbstractGraph.java. Untuk tepi berwajaran, kami mentakrifkan kelas WeightedEdge seperti yang ditunjukkan dalam kod di bawah.
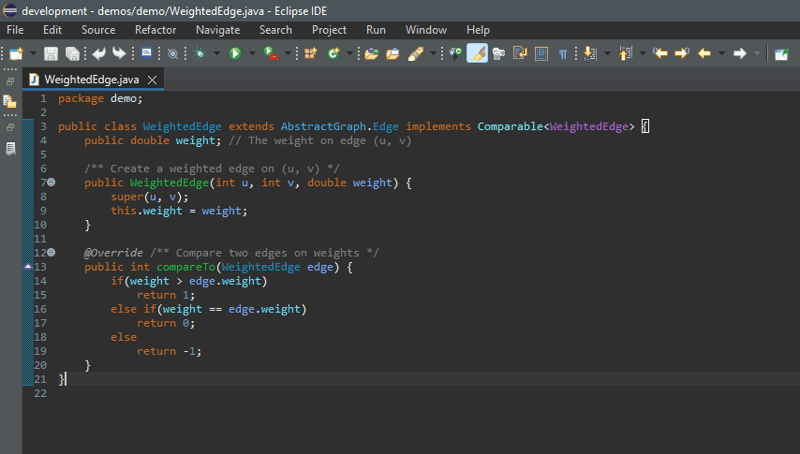
AbstractGraph.Edge ialah kelas dalaman yang ditakrifkan dalam kelas AbstractGraph. Ia mewakili tepi daripada bucu u kepada v. WeightedEdge memanjangkan AbstractGraph.Edge dengan sifat baharu berat.
Untuk mencipta objek WeightedEdge, gunakan WeightedEdge(i, j, w) baharu, dengan w ialah berat di tepi (i , j). Selalunya anda perlu membandingkan berat tepi. Atas sebab ini, kelas WeightedEdge melaksanakan antara muka Setanding.
Untuk graf tidak berwajaran, kami menggunakan senarai bersebelahan untuk mewakili tepi. Untuk graf berwajaran, kami masih menggunakan senarai bersebelahan, senarai bersebelahan untuk bucu dalam graf dalam Rajah di bawah a boleh diwakili seperti berikut:
java.util.List

senarai[i] menyimpan semua tepi bersebelahan dengan bucu i.
Untuk fleksibiliti, kami akan menggunakan senarai tatasusunan dan bukannya tatasusunan bersaiz tetap untuk mewakili senarai seperti berikut:
Senaraikan
Atas ialah kandungan terperinci Mewakili Graf Berwajaran. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
 Bagaimana untuk membaca fail py dalam python
Bagaimana untuk membaca fail py dalam python
 Mengapa saya tidak boleh mengakses penyemak imbas Ethereum?
Mengapa saya tidak boleh mengakses penyemak imbas Ethereum?
 Bagaimana untuk menggunakan pernyataan sisip dalam mysql
Bagaimana untuk menggunakan pernyataan sisip dalam mysql
 bar skrol div
bar skrol div
 Bagaimana untuk mengeksport perkataan daripada powerdesigner
Bagaimana untuk mengeksport perkataan daripada powerdesigner
 Apakah perbezaan antara webstorm dan idea?
Apakah perbezaan antara webstorm dan idea?
 Bagaimana untuk mendaftar di Matcha Exchange
Bagaimana untuk mendaftar di Matcha Exchange
 penggunaan storan setempat
penggunaan storan setempat
 Apakah yang perlu saya lakukan jika iPad saya tidak boleh dicas?
Apakah yang perlu saya lakukan jika iPad saya tidak boleh dicas?




