Kegunaan tidak munasabah numpy&#s einsum

pengenalan

Saya ingin memperkenalkan anda kepada kaedah yang paling berguna dalam Python, np.einsum.

Dengan np.einsum (dan rakan sejawatannya dalam Tensorflow dan JAX), anda boleh menulis operasi matriks dan tensor yang rumit dengan cara yang sangat jelas dan ringkas. Saya juga mendapati bahawa kejelasan dan ringkasnya melegakan banyak beban mental yang datang dengan bekerja dengan tensor.

Dan ia sebenarnya agak mudah untuk dipelajari dan digunakan. Begini caranya:

Dalam np.einsum, anda mempunyai hujah rentetan subskrip dan anda mempunyai satu atau lebih operan:

numpy.einsum(subscripts : string, *operands : List[np.ndarray])

Argumen subskrip ialah "bahasa mini" yang memberitahu numpy cara memanipulasi dan menggabungkan paksi operan. Agak sukar untuk dibaca pada mulanya, tetapi tidaklah buruk apabila anda memahaminya.

Operan Tunggal

Untuk contoh pertama, mari kita gunakan np.einsum untuk menukar paksi (a.k.a. ambil transpose) matriks A:

M = np.einsum('ij->ji', A)

Huruf i dan j diikat pada paksi pertama dan kedua A. Numpy mengikat huruf ke paksi mengikut susunan ia muncul, tetapi numpy tidak peduli huruf yang anda gunakan jika anda jelas. Kita boleh menggunakan a dan b, sebagai contoh, dan ia berfungsi dengan cara yang sama:

M = np.einsum('ab->ba', A)

Walau bagaimanapun, anda mesti membekalkan seberapa banyak huruf yang terdapat paksi dalam operan. Terdapat dua paksi dalam A, jadi anda mesti membekalkan dua huruf yang berbeza. Contoh seterusnya tidak berfungsi kerana formula subskrip hanya mempunyai satu huruf untuk diikat, i:

# broken
M = np.einsum('i->i', A)

Sebaliknya, jika operan memang mempunyai satu paksi sahaja (i.o.w., ia adalah vektor), maka formula subskrip satu huruf berfungsi dengan baik, walaupun ia tidak begitu berguna kerana ia meninggalkan vektor a apa adanya:

m = np.einsum('i->i', a)

Penjumlahan Atas Kapak

Tetapi bagaimana dengan operasi ini? Tiada i di sebelah kanan. Adakah ini sah?

c = np.einsum('i->', a)

Mengejutkan, ya!

Berikut ialah kunci pertama untuk memahami intipati np.einsum: Jika paksi diabaikan dari sebelah kanan, maka paksi itu dijumlahkan.

Kod:

c = 0
I = len(a)
for i in range(I):
   c += a[i]

Tingkah laku penjumlahan tidak terhad kepada satu paksi. Sebagai contoh, anda boleh menjumlahkan dua paksi serentak dengan menggunakan formula subskrip ini: c = np.einsum('ij->', A):

Berikut ialah kod Python yang sepadan untuk sesuatu pada kedua-dua paksi:

c = 0
I,J = A.shape
for i in range(I):
   for j in range(J):
      c += A[i,j]

Tetapi ia tidak berhenti di situ - kita boleh menjadi kreatif dan menjumlahkan beberapa paksi dan meninggalkan yang lain sahaja. Contohnya: np.einsum('ij->i', A) menjumlahkan baris matriks A, meninggalkan vektor jumlah baris panjang j:

Kod:

numpy.einsum(subscripts : string, *operands : List[np.ndarray])

Begitu juga, np.einsum('ij->j', A) menjumlahkan lajur dalam A.

Kod:

M = np.einsum('ij->ji', A)

Dua Operan

Terdapat had untuk perkara yang boleh kita lakukan dengan satu operan. Perkara menjadi lebih menarik (dan berguna) dengan dua operan.

Katakan anda mempunyai dua vektor a = [a_1, a_2, ... ] dan b = [a_1, a_2, ...].

Jika len(a) === len(b), kita boleh mengira hasil dalam (juga dipanggil produk titik) seperti ini:

M = np.einsum('ab->ba', A)

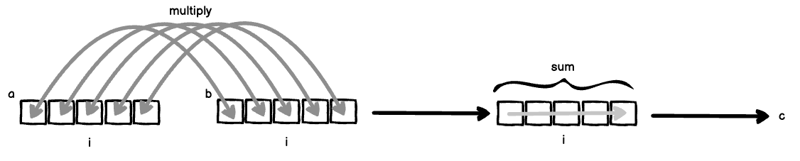
Dua perkara berlaku di sini serentak:

1. Oleh kerana i terikat kepada kedua-dua a dan b, a dan b "berbaris" dan kemudian didarab bersama: a[i] * b[i].
2. Oleh kerana indeks i dikecualikan dari sebelah kanan, paksi i dijumlahkan untuk menghapuskannya.

Jika anda menggabungkan (1) dan (2) bersama, anda akan mendapat produk dalaman klasik.

Kod:

# broken
M = np.einsum('i->i', A)

Sekarang, katakan bahawa kita tidak meninggalkan i daripada formula subskrip, kita akan mendarabkan semua a[i] dan b[i] dan bukan jumlah atas i:

m = np.einsum('i->i', a)

Kod:

c = np.einsum('i->', a)

Ini juga dipanggil pendaraban mengikut unsur (atau Produk Hadamard untuk matriks), dan biasanya dilakukan melalui kaedah numpy np.multiply.

Masih terdapat variasi ketiga formula subskrip, yang dipanggil produk luar.

c = 0
I = len(a)
for i in range(I):
   c += a[i]

Dalam formula subskrip ini, paksi a dan b terikat pada huruf yang berasingan, dan dengan itu dianggap sebagai "pembolehubah gelung" yang berasingan. Oleh itu C mempunyai entri a[i] * b[j] untuk semua i dan j, disusun menjadi matriks.

Kod:

c = 0
I,J = A.shape
for i in range(I):
   for j in range(J):
      c += A[i,j]

Tiga Operan

Melangkah lebih jauh produk luar, berikut ialah versi tiga operan:

I,J = A.shape
r = np.zeros(I)
for i in range(I):
   for j in range(J):
      r[i] += A[i,j]

Kod Python yang setara untuk produk luar tiga operan kami ialah:

I,J = A.shape
r = np.zeros(J)
for i in range(I):
   for j in range(J):
      r[j] += A[i,j]

Melangkah lebih jauh, tiada apa yang menghalang kami daripada meninggalkan paksi untuk menjumlahkan mereka selain memindahkan hasil dengan menulis ki dan bukannya ik di sebelah kanan ->:

numpy.einsum(subscripts : string, *operands : List[np.ndarray])

Kod Python yang setara akan berbunyi:

M = np.einsum('ij->ji', A)

Sekarang saya harap anda boleh mula melihat bagaimana anda boleh menentukan operasi tensor yang rumit dengan lebih mudah. Apabila saya bekerja dengan lebih meluas dengan numpy, saya mendapati diri saya mencapai np.einsum pada bila-bila masa saya terpaksa melaksanakan operasi tensor yang rumit.

Menurut pengalaman saya, np.einsum memudahkan pembacaan kod kemudian - Saya boleh membaca operasi di atas terus dari subskrip: "Hasil keluaran luar tiga vektor, dengan paksi tengah dijumlahkan, dan hasil akhir ditukarkan ". Jika saya terpaksa membaca siri operasi numpy yang rumit, saya mungkin mendapati diri saya terikat.

Contoh Praktikal

Untuk contoh praktikal, mari kita laksanakan persamaan di tengah-tengah LLM, daripada kertas klasik "Perhatian Adalah Semua yang Anda Perlukan".

Pers. 1 menerangkan Mekanisme Perhatian:

Kami akan menumpukan perhatian kami pada istilah $Q{K}^T$QKT , kerana softmax tidak boleh dikira oleh np.einsum dan faktor penskalaan $\frac{1}{\sqrt{d_k}}$dk​​1 ​ adalah remeh untuk memohon.

The $Q{K}^T$QKT istilah mewakili produk titik bagi pertanyaan m dengan kunci n. Q ialah koleksi m vektor baris d-dimensi yang disusun ke dalam matriks, jadi Q mempunyai bentuk md. Begitu juga, K ialah koleksi n vektor baris dimensi d yang disusun ke dalam matriks, jadi K mempunyai bentuk md.

Produk antara Q dan K tunggal akan ditulis sebagai:

np.einsum('md,nd->mn', Q, K)

Perhatikan bahawa kerana cara kami menulis persamaan subskrip kami, kami mengelak daripada perlu menukar K sebelum pendaraban matriks!

Jadi, itu nampaknya agak mudah - sebenarnya, ia hanyalah pendaraban matriks tradisional. Namun, kami belum selesai. Perhatian Adalah Semua yang Anda Perlu menggunakan perhatian berbilang kepala, yang bermaksud kita benar-benar mempunyai k pendaraban matriks sedemikian berlaku serentak pada koleksi matriks Q dan matriks K yang diindeks .

Untuk menjadikan perkara lebih jelas, kami mungkin menulis semula produk sebagai $Q_i{K}_i^T$Qi​K iT​ .

Ini bermakna kita mempunyai paksi tambahan i untuk kedua-dua Q dan K.

Apatah lagi, jika kami berada dalam suasana latihan, kami mungkin melaksanakan batch operasi perhatian berbilang kepala sedemikian.

Jadi berkemungkinan mahu melakukan operasi ke atas kumpulan contoh di sepanjang paksi kelompok b. Oleh itu, produk lengkap adalah seperti:

numpy.einsum(subscripts : string, *operands : List[np.ndarray])

Saya akan melangkau rajah di sini kerana kita berurusan dengan tensor 4 paksi. Tetapi anda mungkin boleh membayangkan "menyusun" rajah awal untuk mendapatkan paksi berbilang kepala kami i, dan kemudian "menyusun" "tindan" itu untuk mendapatkan paksi batch b kami.

Sukar untuk saya melihat bagaimana kami akan melaksanakan operasi sedemikian dengan mana-mana gabungan kaedah numpy yang lain. Namun, dengan sedikit pemeriksaan, jelas perkara yang berlaku: Dalam satu kelompok, atas koleksi matriks Q dan K, lakukan pendaraban matriks Qt(K).

Sekarang, bukankah itu hebat?

Palam tak tahu malu

Setelah melakukan founder mode grind selama setahun, saya sedang mencari kerja. Saya mempunyai lebih 15 tahun pengalaman dalam pelbagai bidang teknikal dan bahasa pengaturcaraan dan juga pengalaman mengurus pasukan. Matematik dan statistik adalah bidang tumpuan. DM saya dan jom bincang!

Atas ialah kandungan terperinci Kegunaan tidak munasabah numpy&#s einsum. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!