
Seorang pembaca catatan blog terakhir saya menunjukkan kepada saya bahawa untuk operasi seperti matmul slicewise, np.einsum jauh lebih perlahan daripada np.matmul melainkan anda menghidupkan bendera optima dalam senarai parameter: np.einsum(.. ., mengoptimumkan = Benar).
Memandangkan agak ragu-ragu, saya menyalakan buku nota Jupyter dan melakukan beberapa ujian awal. Dan saya akan terkutuk, ia benar-benar benar - walaupun untuk kes dua operan di mana pengoptimuman tidak sepatutnya membuat apa-apa perbezaan sama sekali!
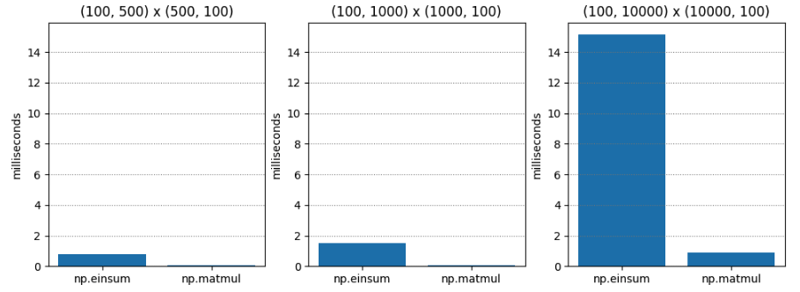
Ujian 1 agak mudah - pendaraban matriks dua matriks tertib-C (aka susunan utama baris) yang berbeza-beza dimensi. np.matmul secara konsisten kira-kira dua puluh kali lebih pantas.
| M1 | M2 | np.einsum | np.matmul | np.einsum / np.matmul |
|---|---|---|---|---|
| (100, 500) | (500, 100) | 0.765 | 0.045 | 17.055 |
| (100, 1000) | (1000, 100) | 1.495 | 0.073 | 20.554 |
| (100, 10000) | (10000, 100) | 15.148 | 0.896 | 16.899 |
Untuk Ujian 2, dengan optimize=True, hasilnya berbeza secara drastik. np.einsum masih lebih perlahan, tetapi paling teruk hanya kira-kira 1.5 kali lebih perlahan!

| M1 | M2 | np.einsum | np.matmul | np.einsum / np.matmul |
|---|---|---|---|---|
| (100, 500) | (500, 100) | 0.063 | 0.043 | 1.474 |
| (100, 1000) | (1000, 100) | 0.086 | 0.067 | 1.284 |
| (100, 10000) | (10000, 100) | 1.000 | 0.936 | 1.068 |
Pemahaman saya tentang bendera optima ialah ia menentukan susunan pengecutan optimum apabila terdapat tiga atau lebih operan. Di sini, kami hanya mempunyai dua operan. Jadi pengoptimuman tidak sepatutnya membuat perbezaan, bukan?
Tetapi mungkin pengoptimuman melakukan sesuatu yang lebih daripada sekadar memilih perintah pengecutan? Mungkin mengoptimumkan mengetahui susun atur memori, dan ini ada kaitan dengan susun atur baris-utama berbanding lajur-utama?
Dalam kaedah pendaraban matriks sekolah gred, untuk mengira satu entri, anda mengulangi satu baris dalam op1 sambil anda mengulangi satu lajur dalam op2, jadi meletakkan hujah kedua dalam susunan lajur-utama mungkin menyebabkan mempercepatkan untuk np.einsum (dengan mengandaikan bahawa np.einsum adalah seperti versi umum kaedah pendaraban matriks sekolah gred di bawah hud, yang saya syak adalah benar).
Jadi, untuk Ujian 3, saya lulus dalam matriks lajur utama untuk operan kedua untuk melihat sama ada ini mempercepatkan np.einsum apabila optimize=False.
Inilah hasilnya. Yang menghairankan, np.einsum masih jauh lebih teruk. Jelas sekali, sesuatu sedang berlaku yang saya tidak faham - mungkin np.einsum menggunakan laluan kod yang sama sekali berbeza apabila pengoptimuman adalah Benar? Masa untuk mula menggali.

| M1 | M2 | np.einsum | np.matmul | np.einsum / np.matmul |
|---|---|---|---|---|
| (100, 500) | (500, 100) | 1.486 | 0.056 | 26.541 |
| (100, 1000) | (1000, 100) | 3.885 | 0.125 | 31.070 |
| (100, 10000) | (10000, 100) | 49.669 | 1.047 | 47.444 |
Nota keluaran Numpy 1.12.0 menyebut pengenalan bendera pengoptimuman. Walau bagaimanapun, tujuan mengoptimumkan nampaknya adalah untuk menentukan susunan hujah dalam rantaian operan digabungkan (iaitu; persekutuan) - jadi pengoptimuman tidak sepatutnya membuat perbezaan untuk hanya dua operan, bukan? Berikut ialah nota keluaran:
np.einsum kini menyokong hujah optima yang akan mengoptimumkan susunan penguncupan. Contohnya, np.einsum akan melengkapkan contoh titik rantai np.einsum(‘ij,jk,kl->il’, a, b, c) dalam satu pas yang akan berskala seperti N^4; walau bagaimanapun, apabila optimize=True np.einsum akan mencipta tatasusunan perantaraan untuk mengurangkan penskalaan ini kepada N^3 atau secara berkesan np.dot(a, b).dot(c). Penggunaan tensor perantaraan untuk mengurangkan penskalaan telah digunakan pada tatatanda penjumlahan einsum am. Lihat np.einsum_path untuk mendapatkan butiran lanjut.
Untuk menambah misteri, beberapa nota keluaran kemudian menunjukkan bahawa np.einsum telah dinaik taraf untuk menggunakan tensordot (yang sendiri menggunakan BLAS jika sesuai). Sekarang, itu nampaknya menjanjikan.
Tetapi, mengapa kita hanya melihat kelajuan apabila pengoptimuman adalah Benar? Apa yang sedang berlaku?
Jika kita membaca def einsum(*operands, out=None, optimize=False, **kwargs) dalam numpy/numpy/_core/einsumfunc.py, kita akan sampai kepada logik keluar awal ini dengan segera:
# If no optimization, run pure einsum
if optimize is False:
if specified_out:
kwargs['out'] = out
return c_einsum(*operands, **kwargs)
Adakah c_einsum menggunakan tensordot? Saya meraguinya. Kemudian dalam kod, kita melihat panggilan tensordot yang nota 1.14 nampaknya merujuk:
# Start contraction loop
for num, contraction in enumerate(contraction_list):
...
# Call tensordot if still possible
if blas:
...
# Contract!
new_view = tensordot(
*tmp_operands, axes=(tuple(left_pos), tuple(right_pos))
)
Jadi, inilah yang berlaku:
Bagi saya, ini kelihatan seperti pepijat. IMHO, "awal keluar" pada permulaan np.einsum masih harus mengesan jika operan serasi tensordot dan memanggil tensordot jika boleh. Kemudian, kami akan mendapat kelajuan BLAS yang jelas walaupun pengoptimuman adalah Palsu. Lagipun, semantik pengoptimuman berkaitan dengan susunan penguncupan, bukan penggunaan BLAS, yang saya fikir harus diberikan.
Faedah di sini ialah orang yang menggunakan np.einsum untuk operasi yang bersamaan dengan doa tensordot akan mendapat kelajuan yang sesuai, yang menjadikan np.einsum agak kurang berbahaya dari sudut prestasi.
Saya menggunakan beberapa kod C untuk menyemaknya. Inti pelaksanaannya ada di sini.
Selepas banyak menghurai hujah dan penyediaan parameter, susunan lelaran paksi ditentukan dan lelaran tujuan khas disediakan. Setiap hasil daripada lelaran mewakili cara yang berbeza untuk melangkah ke atas semua operan secara serentak.
# If no optimization, run pure einsum
if optimize is False:
if specified_out:
kwargs['out'] = out
return c_einsum(*operands, **kwargs)
Dengan mengandaikan pengoptimuman kes khas tertentu tidak digunakan, fungsi jumlah produk (sop) yang sesuai ditentukan berdasarkan jenis data yang terlibat:
# Start contraction loop
for num, contraction in enumerate(contraction_list):
...
# Call tensordot if still possible
if blas:
...
# Contract!
new_view = tensordot(
*tmp_operands, axes=(tuple(left_pos), tuple(right_pos))
)
Kemudian, operasi jumlah produk (sop) ini digunakan pada setiap langkah berbilang operan yang dikembalikan daripada lelaran, seperti yang dilihat di sini:
/* Allocate the iterator */
iter = NpyIter_AdvancedNew(nop+1, op, iter_flags, order, casting, op_flags,
op_dtypes, ndim_iter, op_axes, NULL, 0);
Itu pemahaman saya tentang cara einsum berfungsi, yang diakui masih sedikit nipis - ia benar-benar layak lebih daripada jam yang saya berikan.
Tetapi ia mengesahkan syak wasangka saya, walau bagaimanapun, ia bertindak seperti versi umum gigabrain bagi kaedah pendaraban matriks sekolah gred. Akhirnya, ia mewakilkan kepada satu siri operasi "jumlah produk" yang bergantung pada "striders" yang bergerak melalui operan - tidak terlalu berbeza daripada apa yang anda lakukan dengan jari anda apabila anda mempelajari pendaraban matriks.
Jadi mengapa np.einsum secara amnya lebih pantas apabila anda memanggilnya dengan optimize=True? Ada dua sebab.
Sebab pertama (dan asal) ialah ia cuba mencari laluan penguncupan yang optimum. Walau bagaimanapun, seperti yang saya nyatakan, itu tidak penting apabila kita hanya mempunyai dua operan, seperti yang kita lakukan dalam ujian prestasi kita.
Sebab kedua (dan lebih baharu) ialah apabila optimize=True, walaupun dalam dua kes operan ia mengaktifkan laluan kod yang memanggil tensordot jika boleh, yang seterusnya cuba menggunakan BLAS. Dan BLAS dioptimumkan seperti pendaraban matriks!
Jadi, misteri percepatan dua operan telah diselesaikan! Walau bagaimanapun, kami belum benar-benar merangkumi ciri-ciri percepatan kerana perintah pengecutan. Itu perlu menunggu siaran akan datang! Nantikan!
Atas ialah kandungan terperinci Menyiasat prestasi np.einsum. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
 Akhiran nama fail pengubahsuaian kelompok Linux
Akhiran nama fail pengubahsuaian kelompok Linux
 nilai mutlak python
nilai mutlak python
 Bagaimana untuk memasang sijil ssl
Bagaimana untuk memasang sijil ssl
 Bagaimana untuk mematikan komputer anda dengan cepat
Bagaimana untuk mematikan komputer anda dengan cepat
 Cara menggunakan php sleep
Cara menggunakan php sleep
 Berapakah nilai Dimensity 9000 bersamaan dengan Snapdragon?
Berapakah nilai Dimensity 9000 bersamaan dengan Snapdragon?
 kemas kini penggunaan penyata
kemas kini penggunaan penyata
 Apakah tetapan memori maya yang sesuai?
Apakah tetapan memori maya yang sesuai?




