Songsang Aras Ganjil Pokok Binari-tutorial php-php.cn

2415. Songsang Aras Ganjil Pokok Binari

Kesukaran: Sederhana

Topik: Pokok, Carian Pertama Kedalaman, Carian Luas-Pertama, Pokok Binari

Memandangkan punca pokok perduaan sempurna, terbalikkan nilai nod pada setiap peringkat ganjil pokok itu.

Contohnya, katakan nilai nod pada tahap 3 ialah [2,1,3,4,7,11,29,18], maka ia sepatutnya menjadi [18,29,11,7,4,3,1 ,2].

Kembalikan akar pokok terbalik.

Pokok binari adalah sempurna jika semua nod induk mempunyai dua anak dan semua daun berada pada tahap yang sama.

Tahap nod ialah bilangan tepi di sepanjang laluan antaranya dan nod akar.

Contoh 1:

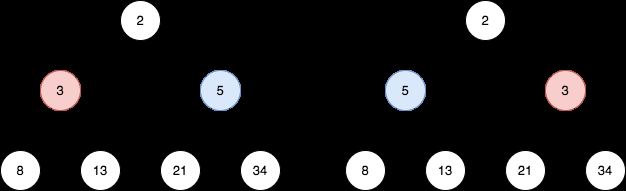
Reverse Odd Levels of Binary Tree

Input: punca = [2,3,5,8,13,21,34]
Output: [2,5,3,8,13,21,34]
Penjelasan:
- Pokok itu hanya mempunyai satu aras ganjil.
- Nod pada tahap 1 masing-masing ialah 3, 5, yang diterbalikkan dan menjadi 5, 3.

Contoh 2:

Reverse Odd Levels of Binary Tree

Input: akar = [7,13,11]
Output: [7,11,13]
Penjelasan:
- Nod pada tahap 1 ialah 13, 11, yang diterbalikkan dan menjadi 11, 13.

Contoh 3:

Input: punca = [0,1,2,0,0,0,0,0,1,1,1,1,2,2,2,2]
Output: [0,2,1,0,0,0,0,2,2,2,2,1,1,1,1]
Penjelasan:
- Tahap ganjil mempunyai nilai bukan sifar.
- Nod pada tahap 1 ialah 1, 2, dan 2, 1 selepas pembalikan.
- Nod pada tahap 3 ialah 1, 1, 1, 1, 2, 2, 2, 2 dan ialah 2, 2, 2, 2, 1, 1, 1, 1 selepas pembalikan.

Kekangan:

Bilangan nod dalam pokok adalah dalam julat [1, 2¹⁴].
0 <= Node.val <= 10⁵
akar ialah pokok binari yang sempurna.

Petunjuk:

Cuba selesaikan secara rekursif untuk setiap peringkat secara bebas.
Semasa melakukan carian mendalam-pertama, lewati nod kiri dan kanan (yang sepatutnya digandingkan) ke peringkat seterusnya. Jika tahap semasa adalah ganjil, kemudian undurkan nilainya, atau pindahkan secara rekursif ke tahap seterusnya.

Penyelesaian:

Kita perlu melakukan traversal depth-first pada pokok binari. Tugasnya adalah untuk membalikkan nilai nod pada tahap ganjil. Pokok binari yang sempurna bermakna semua nod bukan daun mempunyai dua anak dan semua nod daun berada pada tahap yang sama.

Kami akan menggunakan pendekatan DFS (Depth-First Search) dan pada setiap tahap ganjil, kami akan membalikkan nilai nod. Di bawah ialah penyelesaian yang mencapai ini.

Perkara Utama:

Pokoknya sempurna, bermakna ia seimbang sepenuhnya, dan semua nod daun berada pada tahap yang sama.
Hanya nod pada tahap ganjil perlu diterbalikkan. Tahap ganjil diindeks bermula dari tahap 1 (1, 3, 5, dsb.).
DFS boleh digunakan untuk melintasi pokok dan mengenal pasti tahap nod. Apabila kami menghadapi tahap ganjil, kami menukar nilai nod pada tahap itu.
Di setiap peringkat, kami merentasi dua nod anak: anak kiri dan anak kanan.

Pendekatan:

Lakukan rentas pokok yang mendalam terlebih dahulu.
Untuk setiap pasangan nod pada tahap semasa:
- Jika tahapnya ganjil, tukar nilai nod.
Proses anak kiri dan kanan nod semasa secara rekursif, menghantar maklumat tahap yang dikemas kini.
Kembalikan nod akar selepas memproses keseluruhan pokok.

Pelan:

Mulakan dari nod akar.
Gunakan fungsi rekursif dfs untuk melintasi pepohon dan membalikkan nilai nod pada tahap ganjil.
Jejaki tahap semasa untuk mengenal pasti tahap ganjil.
Tukar nilai pada tahap ganjil dan teruskan traversal DFS untuk kanak-kanak.
Kembalikan akar selepas diproses.

Langkah Penyelesaian:

Tentukan fungsi rekursif dfs($left, $right, $isOddLevel):
- kiri: Nod anak kiri.
- kanan: Nod anak kanan.
- isOddLevel: Boolean yang menunjukkan sama ada tahap semasa adalah ganjil.
Semak jika kiri adalah batal. Jika ya, kembalikan, kerana tiada lagi nod untuk diproses.
Jika isOddLevel adalah benar, tukar nilai nod kiri dan kanan.
Panggil fungsi dfs secara rekursif untuk:
- Anak kiri anak kiri dan kanan anak kanan (tingkat seterusnya).
- Anak kanan kiri dan anak kiri kanan (tingkat seterusnya).
Mulakan rekursi dengan dfs($root->left, $root->right, true) dan kembalikan root.

Mari laksanakan penyelesaian ini dalam PHP: 2415. Songsang Aras Ganjil Pokok Binari

<?php
class TreeNode {
    public $val = 0;
    public $left = null;
    public $right = null;

    public function __construct($val = 0, $left = null, $right = null) {
        $this->val = $val;
        $this->left = $left;
        $this->right = $right;
    }
}

class Solution {
    /**
     * @param TreeNode $root
     * @return TreeNode
     */
    public function reverseOddLevels($root) {
       ...
       ...
       ...
       /**
        * go to ./solution.php
        */
    }

    /**
     * Helper function to perform DFS
     *
     * @param $left
     * @param $right
     * @param $isOddLevel
     * @return void
     */
    private function dfs($left, $right, $isOddLevel) {
       ...
       ...
       ...
       /**
        * go to ./solution.php
        */
    }
}

// Example usage:
$root = new TreeNode(2);
$root->left = new TreeNode(3);
$root->right = new TreeNode(5);
$root->left->left = new TreeNode(8);
$root->left->right = new TreeNode(13);
$root->right->left = new TreeNode(21);
$root->right->right = new TreeNode(34);

$solution = new Solution();
$reversedRoot = $solution->reverseOddLevels($root);

// Function to print the tree for testing
function printTree($root) {
    if ($root === null) {
        return;
    }
    echo $root->val . " ";
    printTree($root->left);
    printTree($root->right);
}

printTree($reversedRoot); // Output: 2 5 3 8 13 21 34
?>

Salin selepas log masuk

Penjelasan:

Kelas Nod Pokok: Mewakili struktur nod pokok binari, yang mempunyai nilai (val) dan dua anak (kiri, kanan).
Fungsi reverseOddLevels: Memulakan DFS dengan anak kiri dan kanan nod akar dan bermula pada tahap 1 (tahap ganjil).
Fungsi dfs:
- Mengambil dua nod (kiri dan kanan) dan boolean isOddLevel untuk menentukan sama ada tahap semasa adalah ganjil.
- Jika tahap semasa adalah ganjil, nilai kiri dan kanan ditukar.
- Secara rekursif memanggil dirinya sendiri untuk tahap seterusnya, menukar nilai isOddLevel (true menjadi palsu dan sebaliknya).
Rekursi diteruskan untuk memproses pasangan nod seterusnya pada setiap peringkat, memastikan hanya nod pada tahap ganjil diterbalikkan.

Contoh Panduan:

Contoh 1:

Input:

Salin selepas log masuk

Tahap 0: [2] (sekata, tiada perubahan).
Tahap 1: [3, 5] (ganjil, terbalik kepada [5, 3]).
Tahap 2: [8, 13, 21, 34] (sekata, tiada perubahan).

Output:

Salin selepas log masuk

Contoh 2:

Input:

       7
      / \
     13  11

Salin selepas log masuk

Tahap 0: [7] (sekata, tiada perubahan).
Tahap 1: [13, 11] (ganjil, terbalik kepada [11, 13]).

Output:

       7
      / \
     11  13

Salin selepas log masuk

Kerumitan Masa:

Kerumitan Masa: O(n), dengan n ialah bilangan nod dalam pepohon binari. Kami melawati setiap nod tepat sekali secara mendalam-dahulukan.
Kerumitan Angkasa Lepas: O(h), dengan h ialah ketinggian pokok. Kedalaman rekursi sepadan dengan ketinggian pokok, dan dalam kes yang paling teruk (untuk pokok senget), ia adalah O(n), tetapi untuk pokok binari yang sempurna, ia O(log n).

Penyelesaian ini dengan cekap membalikkan nod pada tahap ganjil pepohon binari yang sempurna menggunakan carian mendalam-pertama dengan kerumitan masa O(n). Kod menukar nilai pada tahap ganjil dan menggunakan pendekatan rekursif untuk memproses pokok.

Pautan Kenalan

Jika anda mendapati siri ini membantu, sila pertimbangkan untuk memberi repositori bintang di GitHub atau berkongsi siaran pada rangkaian sosial kegemaran anda ?. Sokongan anda amat bermakna bagi saya!

Jika anda mahukan kandungan yang lebih berguna seperti ini, sila ikuti saya: