
Apabila bekerja dengan JavaScript, menulis kod berfungsi adalah penting, tetapi memastikan ia berjalan dengan cekap adalah sama penting. Di sinilah Notasi Big O masuk. Ia menyediakan cara untuk menganalisis cara skala prestasi kod anda apabila saiz input meningkat, membantu anda menulis aplikasi yang dioptimumkan dan boleh skala.
Artikel ini akan meneroka asas Notasi Big O dan kerumitan masa biasa dengan contoh mesra pemula dalam JavaScript
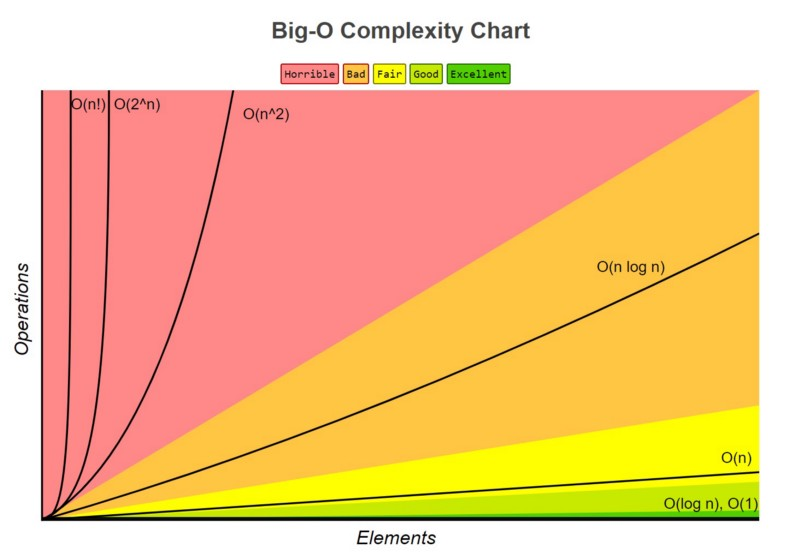
Notasi O Besar ialah perwakilan matematik yang menerangkan kecekapan algoritma. Ia membantu kami memahami:
Matlamatnya adalah untuk menilai prestasi algoritma apabila saiz input berkembang, memfokuskan pada senario terburuk.
Katakan anda ditugaskan untuk mencari nama dalam buku telefon:
Kedua-dua pendekatan menyelesaikan masalah, tetapi kecekapannya berbeza dengan ketara apabila saiz buku telefon bertambah. Big O membantu kami membandingkan pendekatan ini dan memilih yang terbaik.
Di bawah ialah kerumitan Big O biasa, dijelaskan dengan contoh praktikal dalam JavaScript.
Masa jalan kekal sama tanpa mengira saiz input. Operasi ini adalah yang paling cekap.
Contoh: Mengakses elemen dalam tatasusunan mengikut indeks.
const numbers = [10, 20, 30, 40, 50]; console.log(numbers[2]); // Always takes the same time, no matter the array size
Masa jalan berkembang secara logaritma apabila saiz input bertambah. Ini sering berlaku dalam algoritma bahagi-dan-takluk seperti carian binari.
Contoh: Carian binari pada tatasusunan yang diisih.
function binarySearch(arr, target) {
let start = 0;
let end = arr.length - 1;
while (start <= end) {
const mid = Math.floor((start + end) / 2);
if (arr[mid] === target) {
return mid;
} else if (arr[mid] < target) {
start = mid + 1; // Search the right half
} else {
end = mid - 1; // Search the left half
}
}
return -1; // Target not found
}
const arr = [1, 3, 5, 7, 9];
console.log(binarySearch(arr, 7)); // Output: 3
Masa jalan berkembang secara berkadar dengan saiz input. Ini berlaku apabila anda perlu memeriksa setiap elemen sekali.
Contoh: Mencari item dalam tatasusunan yang tidak diisih.
function linearSearch(arr, target) {
for (let i = 0; i < arr.length; i++) {
if (arr[i] === target) {
return i; // Found
}
}
return -1; // Not found
}
const items = [10, 20, 30, 40, 50];
console.log(linearSearch(items, 30)); // Output: 2
Masa jalan berkembang secara kuadratik apabila saiz input meningkat. Ini adalah tipikal dalam algoritma dengan gelung bersarang.
Contoh: Pelaksanaan isihan gelembung asas.
const numbers = [10, 20, 30, 40, 50]; console.log(numbers[2]); // Always takes the same time, no matter the array size
Waktu jalan berganda dengan setiap input tambahan. Ini berlaku dalam algoritma yang menyelesaikan masalah secara rekursif, dengan mengambil kira semua penyelesaian yang mungkin.
Contoh: Mengira nombor Fibonacci secara rekursif.
function binarySearch(arr, target) {
let start = 0;
let end = arr.length - 1;
while (start <= end) {
const mid = Math.floor((start + end) / 2);
if (arr[mid] === target) {
return mid;
} else if (arr[mid] < target) {
start = mid + 1; // Search the right half
} else {
end = mid - 1; // Search the left half
}
}
return -1; // Target not found
}
const arr = [1, 3, 5, 7, 9];
console.log(binarySearch(arr, 7)); // Output: 3
Begini perbandingan kerumitan Big O yang berbeza apabila saiz input meningkat:
| Big O | Name | Example Use Case | Growth Rate |
|---|---|---|---|
| O(1) | Constant | Array access | Flat |
| O(log n) | Logarithmic | Binary search | Slow growth |
| O(n) | Linear | Looping through an array | Moderate growth |
| O(n²) | Quadratic | Nested loops | Rapid growth |
| O(2ⁿ) | Exponential | Recursive brute force | Very fast growth |
Bayangkan anda sedang menyelesaikan masalah, dan saiz input bertambah. Begini cara algoritma dengan skala kerumitan berbeza apabila saiz input meningkat:
| Input Size | O(1) | O(log n) | O(n) | O(n²) | O(2ⁿ) |
|---|---|---|---|---|---|
| 1 | 1 ms | 1 ms | 1 ms | 1 ms | 1 ms |
| 10 | 1 ms | 3 ms | 10 ms | 100 ms | ~1 sec |
| 100 | 1 ms | 7 ms | 100 ms | 10 sec | ~centuries |
| 1000 | 1 ms | 10 ms | 1 sec | ~17 min | Unrealistic |
Berikut ialah cara untuk menggambarkan bilangan operasi untuk kerumitan yang berbeza menggunakan pembilang mudah:
const numbers = [10, 20, 30, 40, 50]; console.log(numbers[2]); // Always takes the same time, no matter the array size
Big O Notation ialah alat penting untuk menilai kecekapan algoritma dan memahami cara skala kod anda. Dengan memahami asas dan menganalisis corak biasa, anda akan berjaya menulis aplikasi JavaScript yang berprestasi.
Selamat pengekodan! ?
Atas ialah kandungan terperinci Memahami Notasi Big O dan Kerumitan Masa dalam JavaScript. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
 Bagaimana untuk membenamkan gaya CSS dalam HTML
Bagaimana untuk membenamkan gaya CSS dalam HTML
 Sepuluh kedudukan pertukaran mata wang digital teratas
Sepuluh kedudukan pertukaran mata wang digital teratas
 Apakah pernyataan untuk memadam jadual dalam sql
Apakah pernyataan untuk memadam jadual dalam sql
 rangka kerja rangkaian
rangka kerja rangkaian
 Bagaimana untuk mendapatkan panjang tatasusunan dalam js
Bagaimana untuk mendapatkan panjang tatasusunan dalam js
 Perisian sistem pengurusan harta
Perisian sistem pengurusan harta
 tiada penyelesaian fail sedemikian
tiada penyelesaian fail sedemikian
 Maksud volum paparan tajuk hari ini
Maksud volum paparan tajuk hari ini
 Tiada perkhidmatan pada data mudah alih
Tiada perkhidmatan pada data mudah alih




