求斐波那契(Fibonacci)数列通项的七种实现方法

一：递归实现
使用公式f[n]=f[n-1]+f[n-2]，依次递归计算，递归结束条件是f[1]=1，f[2]=1。
二：数组实现
空间复杂度和时间复杂度都是0(n)，效率一般，比递归来得快。
三：vector实现
时间复杂度是0(n)，时间复杂度是0(1)，就是不知道vector的效率高不高，当然vector有自己的属性会占用资源。
四：queue实现
当然队列比数组更适合实现斐波那契数列，时间复杂度和空间复杂度和vector一样，但队列太适合这里了，
f(n)=f(n-1)+f(n-2)，f(n)只和f(n-1)和f(n-2)有关，f(n)入队列后，f(n-2)就可以出队列了。
五：迭代实现
迭代实现是最高效的，时间复杂度是0(n)，空间复杂度是0(1)。
六：公式实现
百度的时候，发现原来斐波那契数列有公式的，所以可以使用公式来计算的。
由于double类型的精度还不够，所以程序算出来的结果会有误差，如果把公式展开计算，得出的结果就是正确的。
完整的实现代码如下：

#include "iostream"
#include "queue"
#include "cmath"
using namespace std;
int fib1(int index)     //递归实现
{
 if(index<1)
 {
  return -1;
 }
 if(index==1 || index==2)
  return 1;
 return fib1(index-1)+fib1(index-2);
}
int fib2(int index)     //数组实现
{
 if(index<1)
 {
  return -1;
 }
 if(index<3)
 {
  return 1;
 }
 int *a=new int[index];
 a[0]=a[1]=1;
 for(int i=2;i<index;i++)
  a[i]=a[i-1]+a[i-2];
 int m=a[index-1];
 delete a;         //释放内存空间
 return m;
}
int fib3(int index)           //借用vector<int>实现
{
 if(index<1)
 {
  return -1;
 }
 vector<int> a(2,1);      //创建一个含有2个元素都为1的向量
 a.reserve(3);
 for(int i=2;i<index;i++)
 {
  a.insert(a.begin(),a.at(0)+a.at(1));
  a.pop_back();
 }
 return a.at(0);
} 
int fib4(int index)       //队列实现
{
 if(index<1)
 {
  return -1;
 }
 queue<int>q;
 q.push(1);
 q.push(1);
 for(int i=2;i<index;i++)
 {
  q.push(q.front()+q.back());
  q.pop();
 }
 return q.back();
}
int fib5(int n)          //迭代实现
{
 int i,a=1,b=1,c=1;
 if(n<1)
 {
  return -1;
 }
 for(i=2;i<n;i++)
 {
  c=a+b;     //辗转相加法（类似于求最大公约数的辗转相除法）
  a=b;
  b=c;
 }
 return c;
}
int fib6(int n)
{
 double gh5=sqrt((double)5);
 return (pow((1+gh5),n)-pow((1-gh5),n))/(pow((double)2,n)*gh5);
} 
int main(void)
{
 printf("%d\n",fib3(6));
 system("pause");
 return 0;
}

七：二分矩阵方法

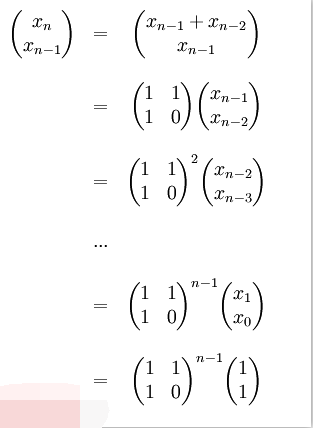
如上图，Fibonacci 数列中任何一项可以用矩阵幂算出，而n次幂是可以在logn的时间内算出的。
下面贴出代码：

void multiply(int c[2][2],int a[2][2],int b[2][2],int mod)
{
 int tmp[4];
 tmp[0]=a[0][0]*b[0][0]+a[0][1]*b[1][0];
 tmp[1]=a[0][0]*b[0][1]+a[0][1]*b[1][1];
 tmp[2]=a[1][0]*b[0][0]+a[1][1]*b[1][0];
 tmp[3]=a[1][0]*b[0][1]+a[1][1]*b[1][1];
 c[0][0]=tmp[0]%mod;
 c[0][1]=tmp[1]%mod;
 c[1][0]=tmp[2]%mod;
 c[1][1]=tmp[3]%mod;
}//计算矩阵乘法，c=a*b
int fibonacci(int n,int mod)//mod表示数字太大时需要模的数
{
 if(n==0)return 0;
 else if(n<=2)return 1;//这里表示第0项为0，第1，2项为1
 int a[2][2]={{1,1},{1,0}};
 int result[2][2]={{1,0},{0,1}};//初始化为单位矩阵
 int s;
 n-=2;
 while(n>0)
 {
  if(n%2 == 1)
   multiply(result,result,a,mod);
  multiply(a,a,a,mod);
  n /= 2;
 }//二分法求矩阵幂
 s=(result[0][0]+result[0][1])%mod;//结果
 return s;
}

附带的再贴上二分法计算a的n次方函数。

int pow(int a,int n)
{
 int ans=1;
 while(n)
 {
  if(n&1)
   ans*=a;
  a*=a;
  n>>=1;
 }
 return ans;
}

更多求斐波那契(Fibonacci)数列通项的七种实现方法相关文章请关注PHP中文网！