
之前简单介绍了动态规划的概念和解题步骤,但是学习中感觉动态规划的应用范围太灵活了,这里就挑一些常见的题目多练习一下。
1、最长公共子序列(字符串相关)
给出两个字符串,找到最长公共子序列(LCS),返回LCS的长度。例如:
例如:给出"ABCD"和"EDCA",这个LCS是 "A"(或 D或C),返回1;
给出"ABCD" 和 "EACB",这个LCS是"AC"返回2。
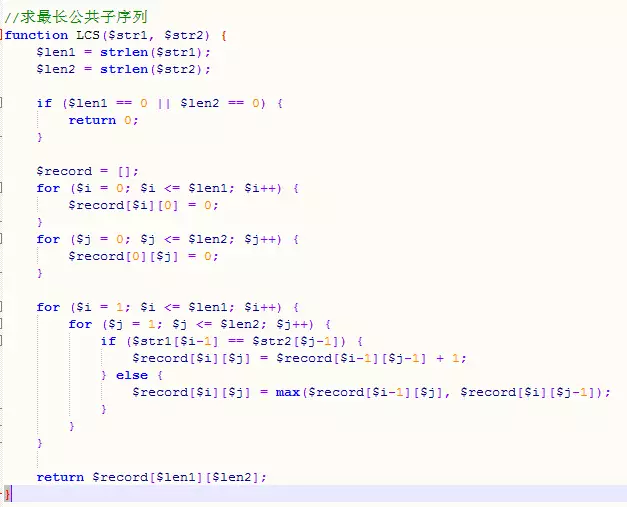
思路:长度为m的字符串a和长度为n的字符串b,他们的最长公共子序列longest[m][n]可通过m-1长度的a和n-1长度的b推得:当a[m]等于b[n]的时候,longest[m][n] = longest[m-1][n-1] + 1;当a[m]不等于b[n]时,longest[m][n]=max(longest[m-1][n], longest[m][n-1])。当字符串a或者b为空字符串时,它与另一个字符串的最长公共子序列必然是0。最后题目的解即为longest[strlen(a)][strlen(b)]。
代码:
2、编辑距离(字符串相关)
给出两个单词word1和word2,计算出将word1 转换为word2的最少操作次数。
你总共三种操作方法:插入一个字符、删除一个字符、替换一个字符。
例如:给出 work1="mart" 和 work2="karma",返回 3。
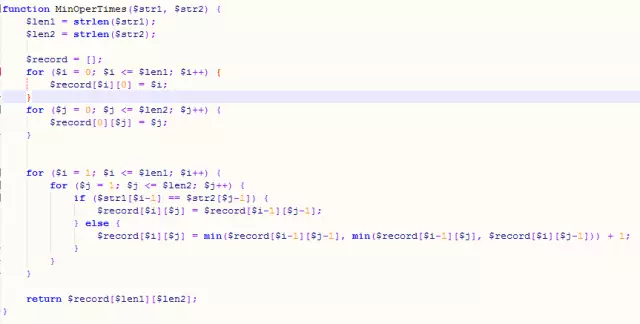
思路:对于长度为m的字符串a和长度为n的字符串b(m、n都大于0),如果a[m]不等于b[n],那么a变为b的最小操作次数=min(a[m-1]变为b[n]的最小操作次数+1,a[m]变为b[n-1]的最小操作次数+1,a[m-1]变为b[n-1]的最小操作次数);如果a[m]等于b[n],那么a[m]变为b[n]的最小操作次数=a[m-1]变为b[n-1]的最小操作次数。
代码:
3、背包问题
给出n个物品的体积A[i]和其价值V[i],将他们装入一个大小为m的背包,最多能装入的总价值有多大?
例如:对于物品体积[2, 3, 5, 7]和对应的价值[1, 5, 2, 4], 假设背包大小为10的话,最大能够装入的价值为9。
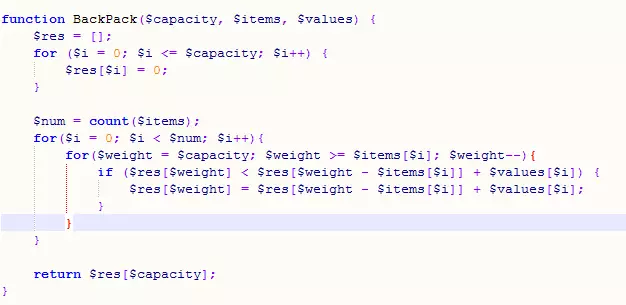
思路:当空间为v时,对于任意一个物品i,如果i可以放入(v大于等于weight[i]),则此时v空间的价值f(v)等于f(v-weight[i]) + values[i],因此通过遍历全部物品可以找到在空间为v时所能得到的最大值。
代码:
4、区间问题(谷歌面试题)
有n个硬币排成一条线,每一枚硬币有不同的价值。两个参赛者轮流一从任意一边取一枚硬币,直到没有硬币为止。计算拿到的硬币总价值,价值最高的获胜。请判定第一个玩家是输还是赢?
例如:给定数组[3,2,2],返回true;给定数组[1,20,15],返回false。
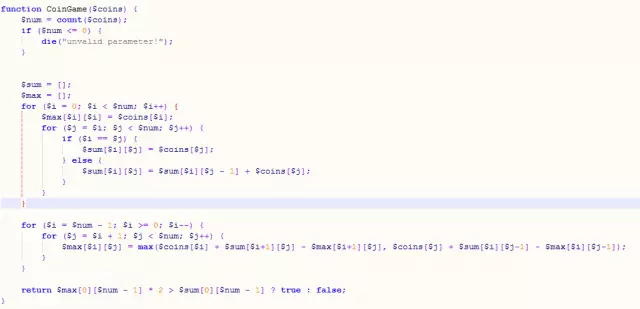
思路:对于给定的一个闭区间(i到j,j大于等于i),玩家A拿硬币只有两种拿法,从左拿或者从右拿。如果从左拿,则A能拿到的最大面值=拿到的这枚硬币的面值 + 剩余区间的总面值 - B玩家在剩余区间能拿到的最大面值;A从右拿的情况与从左拿类似。由此我们可以得到状态转移方程。而通过两次循环我们能够得到长度为n的序列里任意i到j区间的面值总和,以及j=i的情况下先手玩家拿到的最大值(即第i个硬币的面值)。
代码:
以上就是php算法学习之之动态规划(二)的内容,更多相关内容请关注PHP中文网(www.php.cn)!
 Bagaimana untuk membuka fail php
Bagaimana untuk membuka fail php
 Bagaimana untuk mengalih keluar beberapa elemen pertama tatasusunan dalam php
Bagaimana untuk mengalih keluar beberapa elemen pertama tatasusunan dalam php
 Apa yang perlu dilakukan jika penyahserialisasian php gagal
Apa yang perlu dilakukan jika penyahserialisasian php gagal
 Bagaimana untuk menyambungkan php ke pangkalan data mssql
Bagaimana untuk menyambungkan php ke pangkalan data mssql
 Bagaimana untuk menyambung php ke pangkalan data mssql
Bagaimana untuk menyambung php ke pangkalan data mssql
 Bagaimana untuk memuat naik html
Bagaimana untuk memuat naik html
 Bagaimana untuk menyelesaikan aksara bercelaru dalam PHP
Bagaimana untuk menyelesaikan aksara bercelaru dalam PHP
 Bagaimana untuk membuka fail php pada telefon bimbit
Bagaimana untuk membuka fail php pada telefon bimbit




