从无限极分类内存占用看“递归”

在PHP的无限级分类中，用到的很多方法都是递归，但是我们对递归的理解还很模糊，我们接下来就深入理解下递归的优缺点，让大家能有个全面的认识。

什么是递归？

定义

递归（英语：Recursion），又译为递回，在数学与计算机科学中，是指在函数的定义中使用函数自身的方法。

英文的Recursion从词源上分析只是"re-  (again)" + "curs- （come, happen）" 也就是重复发生，再次重现的意思。 而对应的中文翻译 ”递归“ 却表达了两个意思：”递“＋”归“。 这两个意思，正是递归思想的精华所在。从这层次上来看，中文翻译反而更达意。

在网上看到个又去的比喻：

假设你在一个电影院，你想知道自己坐在哪一排，但是前面人很多，你懒得去数了，于是你问前一排的人「你坐在哪一排？」，这样前面的人 (代号 A) 回答你以后，你就知道自己在哪一排了——只要把 A 的答案加一，就是自己所在的排了。不料 A 比你还懒，他也不想数，于是他也问他前面的人 B「你坐在哪一排？」，这样 A 可以用和你一模一样的步骤知道自己所在的排。然后 B 也如法炮制。直到他们这一串人问到了最前面的一排，第一排的人告诉问问题的人「我在第一排」。最后大家就都知道自己在哪一排了。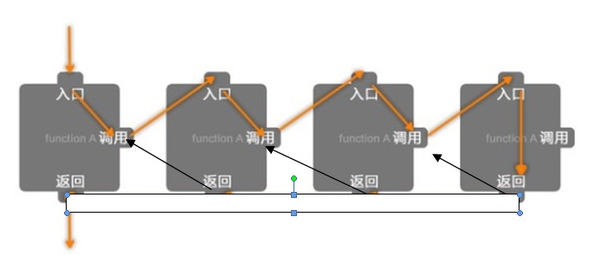

跟循环的区别

单看上面wiki的定义，貌似跟通常所说的无限死循环很像，他们的区别在哪？

递归是静中有动，有去有回。
循环是动静如一，有去无回。

举个例子，给你一把钥匙，你站在门前面，问你用这把钥匙能打开几扇门。

递归：你打开面前这扇门，看到屋里面还有一扇门（这门可能跟前面打开的门一样大小（静），也可能门小了些（动）），你走过去，发现手中的钥匙还可以打开它，你推开门，发现里面还有一扇门，你继续打开，。。。， 若干次之后，你打开面前一扇门，发现只有一间屋子，没有门了。 你开始原路返回，每走回一间屋子，你数一次，走到入口的时候，你可以回答出你到底用这钥匙开了几扇门。

循环：你打开面前这扇门，看到屋里面还有一扇门，（这门可能跟前面打开的门一样大小（静），也可能门小了些（动）），你走过去，发现手中的钥匙还可以打开它，你推开门，发现里面还有一扇门，（前面门如果一样，这门也是一样，第二扇门如果相比第一扇门变小了，这扇门也比第二扇门变小了（动静如一，要么没有变化，要么同样的变化）），你继续打开这扇门，。。。，一直这样走下去。 入口处的人始终等不到你回去告诉他答案。

递归思想

递归就是有去（递去）有回（归来）。

具体来说，为什么可以”有去“？
这要求递归的问题需要是可以用同样的解题思路来回答类似但略有不同的问题（上面例子中的那一把钥匙可以开后面门上的锁）。

为什么可以”有回“？
这要求这些问题不断从大到小，从近及远的过程中，会有一个终点，一个临界点，一个baseline，一个你到了那个点就不用再往更小，更远的地方走下去的点，然后从那个点开始，原路返回到原点。

递归的基本思想是把规模大的问题转化为规模小的相似的子问题来解决。在函数实现时，因为解决大问题的方法和解决小问题的方法往往是同一个方法，所以就产生了函数调用它自身的情况。另外这个解决问题的函数必须有明显的结束条件，这样就不会产生无限递归的情况了。

什么时候需要用递归？

当有些问题的定义本身就是递归形式的时候，最是适合用递归来解决。

计算机专业的同学最最熟悉的莫过于”树“的定义了[4,5]。还有一些定义，比如阶乘，Fibonacci数列[6]，等等。用递归来解决这些问题，往往几行代码就搞定了一些看起来相当”吓人“的问题。 当然，递归的性能问题是另一回事，栈的分配，函数调用代价都是在具体工程实践中要考虑的。 但现在只是讨论递归思想的话，不妨先放下那些，欣赏下递归的美。

---

递归在解决某些问题的时候使得我们思考的方式得以简化，代码也更加精炼，容易阅读。那么既然递归有这么多的优点，我们是不是什么问题都要用递归来解决呢？难道递归就没有缺点吗？今天我们就来讨论一下递归的不足之处。谈到递归就不得不面对它的效率问题。

为什么递归的效率低效？

还是拿斐波那契（Fibonacci）数列来做例子。在很多教科书或文章中涉及到递归或计算复杂性的地方都会将计算斐波那契数列的程序作为经典示例。如果现在让你以最快的速度用C#写出一个计算斐波那契数列第n个数的函数（不考虑参数小于1或结果溢出等异常情况），我不知你的程序是否会和下列代码类似：

public static ulong Fib(ulong n)
{
    return (n == 1 || n == 2) ? 1 : Fib(n - 1) + Fib(n - 2);
}

这段代码应该算是短小精悍（执行代码只有一行），直观清晰，而且非常符合许多程序员的代码美学，许多人在面试时写出这样的代码可能心里还会暗爽。但是如果用这段代码试试计算Fib(1000)我想就再也爽不起来了，它的运行时间也许会让你抓狂。

看来好看的代码未必中用，如果程序在效率不能接受那美观神马的就都是浮云了。如果简单分析一下程序的执行流，就会发现问题在哪，以计算Fibonacci(5)为例：

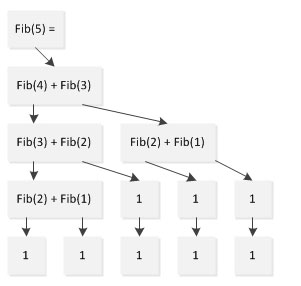
从上图可以看出，在计算Fib(5)的过程中，Fib(1)计算了两次、Fib(2)计算了3次，Fib(3)计算了两次，本来只需要5次计算就可以完成的任务却计算了9次。这个问题随着规模的增加会愈发凸显，以至于Fib(1000)已经无法再可接受的时间内算出。

我们当时使用的是简单的用定义来求 fib(n)，也就是使用公式 fib(n) = fib(n-1) + fib(n-2)。这样的想法是很容易想到的，可是仔细分析一下我们发现，当调用fib(n-1)的时候，还要调用fib(n-2)，也就是说fib(n-2)调用了两次，同样的道理，调用f(n-2)时f(n-3)也调用了两次，而这些冗余的调用是完全没有必要的。可以计算这个算法的复杂度是指数级的。

改进的斐波那契递归算法

那么计算斐波那契数列是否有更好的递归算法呢？ 当然有。让我们来观察一下斐波那契数列的前几项：

11, 1, 2, 3, 5, 8, 13, 21, 34, 55 …

注意到没有，如果我们去掉前面一项，得到的数列依然满足f(n) = f(n-1) – f(n-2), (n>2)，而我们得到的数列是以1，2开头的。很容易发现这个数列的第n-1项就是原数列的第n项。怎么样，知道我们该怎么设计算法了吧？我们可以写这样的一个函数，它接受三个参数，前两个是数列的开头两项，第三个是我们想求的以前两个参数开头的数列的第几项。

1int fib_i(int a, int b, int n);

在函数内部我们先检查n的值，如果n为3则我们只需返回a+b即可，这是简单情境。如果n>3，那么我们就调用f(b, a+b, n-1)，这样我们就缩小了问题的规模（从求第n项变成求第n-1项）。好了，最终代码如下：

int fib_i(int a, int b , int n)
{
    if(n == 3)
        return a+b;
    else
        return fib_i(b, a+b, n-1);
}

为什么对内存有很大的开销？

递归的原理是：先将要计算的变量值存到堆栈中，依次循环，直到递归结束条件满足时，才从堆栈中取出要计算的变量值，计算得到最终结果。
打个比喻：要计算   10！=
递归的话，过程：10！=10 * 9!
               9!=9 * 8!
               ……
                 2！=2 *1！
                 1！=1
计算时，它是将一个一个表达式存到内存，直到递归条件满足1！=1，这样再从内存中取出刚才存的表达式，得出最终的结果。这样的话，会花销更大的系统资源。

而且系统会设置最大递归深度。大于该深度时，就报错退出。函数递归调用过程中，函数中的参数，返回值等会不停的压栈。函数调用会不停地使用栈，报存现场，恢复现场，所以内存开销会越来越大，解决的方法是为尾递归，但是，PHP对尾递归没有优化效果，所以这个解决办法没有什么实际意义。