SPFA算法使用教程
适用范围:给定的图存在负权边,这时类似Dijkstra等算法便没有了用武之地,而Bellman-Ford算法的复杂度又过高,SPFA算法便 派上用场了。 我们约定有向加权图G不存在负权回路,即最短路径一定存在。当然,我们可以在执行该算法前做一次拓扑排序,以判断是否存在负权回路,但这不是我们讨论的重 点。
算法思想:我们用数组d记录每个结点的最短路径估计值,用邻接表来存储图G。我们采取的方法是动态逼近法:设立一个先进先出的队列用来保存待优化的 结点,优化时每次取出队首结点u,并且用u点当前的最短路径估计值对离开u点所指向的结点v进行松弛操作,如果v点的最短路径估计值有所调整,且v点不在 当前的队列中,就将v点放入队尾。这样不断从队列中取出结点来进行松弛操作,直至队列空为止
期望的时间复杂度O(ke), 其中k为所有顶点进队的平均次数,可以证明k一般小于等于2。
实现方法:
建立一个队列,初始时队列里只有起始点,再建立一个表格记录起始点到所有点的最短路径(该表格的初始值要赋为极大值,该点到他本身的路径赋为 0)。然后执行松弛操作,用队列里有的点作为起始点去刷新到所有点的最短路,如果刷新成功且被刷新点不在队列中则把该点加入到队列最后。重复执行直到队列 为空。
判断有无负环:
如果某个点进入队列的次数超过N次则存在负环(SPFA无法处理带负环的图)
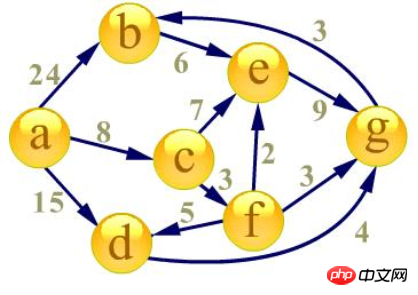
首先建立起始点a到其余各点的
最短路径表格
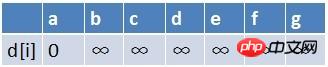
首先源点a入队,当队列非空时:
1、队首元素(a)出队,对以a为起始点的所有边的终点依次进行松弛操作(此处有b,c,d三个点),此时路径表格状态为:
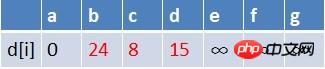
在松弛时三个点的最短路径估值变小了,而这些点队列中都没有出现,这些点
需要入队,此时,队列中新入队了三个结点b,c,d
队首元素b点出队,对以b为起始点的所有边的终点依次进行松弛操作(此处只有e点),此时路径表格状态为:
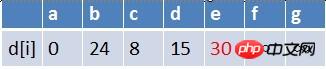
在最短路径表中,e的最短路径估值也变小了,e在队列中不存在,因此e也要
入队,此时队列中的元素为c,d,e
队首元素c点出队,对以c为起始点的所有边的终点依次进行松弛操作(此处有e,f两个点),此时路径表格状态为:

在最短路径表中,e,f的最短路径估值变小了,e在队列中存在,f不存在。因此
e不用入队了,f要入队,此时队列中的元素为d,e,f
队首元素d点出队,对以d为起始点的所有边的终点依次进行松弛操作(此处只有g这个点),此时路径表格状态为:
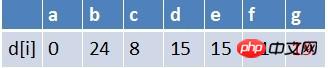
在最短路径表中,g的最短路径估值没有变小(松弛不成功),没有新结点入队,队列中元素为f,g
队首元素f点出队,对以f为起始点的所有边的终点依次进行松弛操作(此处有d,e,g三个点),此时路径表格状态为:
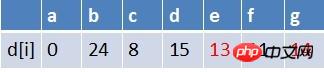
在最短路径表中,e,g的最短路径估值又变小,队列中无e点,e入队,队列中存在g这个点,g不用入队,此时队列中元素为g,e
队首元素g点出队,对以g为起始点的所有边的终点依次进行松弛操作(此处只有b点),此时路径表格状态为:
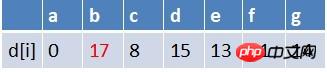
在最短路径表中,b的最短路径估值又变小,队列中无b点,b入队,此时队列中元素为e,b
队首元素e点出队,对以e为起始点的所有边的终点依次进行松弛操作(此处只有g这个点),此时路径表格状态为:
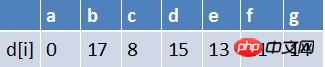
在最短路径表中,g的最短路径估值没变化(松弛不成功),此时队列中元素为b
队首元素b点出队,对以b为起始点的所有边的终点依次进行松弛操作(此处只有e这个点),此时路径表格状态为:

在最短路径表中,e的最短路径估值没变化(松弛不成功),此时队列为空了
最终a到g的最短路径为14
java代码
package spfa负权路径;
import java.awt.List;
import java.util.ArrayList;
import java.util.Scanner;
public class SPFA {
/**
* @param args
*/
public long[] result; //用于得到第s个顶点到其它顶点之间的最短距离
//数组实现邻接表存储
class edge{
public int a;//边的起点
public int b;//边的终点
public int value;//边的值
public edge(int a,int b,int value){
this.a=a;
this.b=b;
this.value=value;
}
}
public static void main(String[] args) {
// TODO Auto-generated method stub
SPFA spafa=new SPFA();
Scanner scan=new Scanner(System.in);
int n=scan.nextInt();
int s=scan.nextInt();
int p=scan.nextInt();
edge[] A=new edge[p];
for(int i=0;i<p;i++){
int a=scan.nextInt();
int b=scan.nextInt();
int value=scan.nextInt();
A[i]=spafa.new edge(a,b,value);
}
if(spafa.getShortestPaths(n,s,A)){
for(int i=0;i<spafa.result.length;i++){
System.out.println(spafa.result[i]+" ");
}
}else{
System.out.println("存在负环");
}
}
/*
* 参数n:给定图的顶点个数
* 参数s:求取第s个顶点到其它所有顶点之间的最短距离
* 参数edge:给定图的具体边
* 函数功能:如果给定图不含负权回路,则可以得到最终结果,如果含有负权回路,则不能得到最终结果
*/
private boolean getShortestPaths(int n, int s, edge[] A) {
// TODO Auto-generated method stub
ArrayList<Integer> list = new ArrayList<Integer>();
result=new long[n];
boolean used[]=new boolean[n];
int num[]=new int[n];
for(int i=0;i<n;i++){
result[i]=Integer.MAX_VALUE;
used[i]=false;
}
result[s]=0;//第s个顶点到自身距离为0
used[s]=true;//表示第s个顶点进入数组队
num[s]=1;//表示第s个顶点已被遍历一次
list.add(s); //第s个顶点入队
while(list.size()!=0){
int a=list.get(0);//获取数组队中第一个元素
list.remove(0);//删除数组队中第一个元素
for(int i=0;i<A.length;i++){
//当list数组队的第一个元素等于边A[i]的起点时
if(a==A[i].a&&result[A[i].b]>(result[A[i].a]+A[i].value)){
result[A[i].b]=result[A[i].a]+A[i].value;
if(!used[A[i].b]){
list.add(A[i].b);
num[A[i].b]++;
if(num[A[i].b]>n){
return false;
}
used[A[i].b]=true;//表示边A[i]的终点b已进入数组队
}
}
}
used[a]=false; //顶点a出数组对
}
return true;
}
}
Atas ialah kandungan terperinci SPFA算法使用教程. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1376
1376
 52
52
 CLIP-BEVFormer: Selia secara eksplisit struktur BEVFormer untuk meningkatkan prestasi pengesanan ekor panjang
Mar 26, 2024 pm 12:41 PM
CLIP-BEVFormer: Selia secara eksplisit struktur BEVFormer untuk meningkatkan prestasi pengesanan ekor panjang
Mar 26, 2024 pm 12:41 PM
Ditulis di atas & pemahaman peribadi penulis: Pada masa ini, dalam keseluruhan sistem pemanduan autonomi, modul persepsi memainkan peranan penting Hanya selepas kenderaan pemanduan autonomi yang memandu di jalan raya memperoleh keputusan persepsi yang tepat melalui modul persepsi boleh Peraturan hiliran dan. modul kawalan dalam sistem pemanduan autonomi membuat pertimbangan dan keputusan tingkah laku yang tepat pada masanya dan betul. Pada masa ini, kereta dengan fungsi pemanduan autonomi biasanya dilengkapi dengan pelbagai penderia maklumat data termasuk penderia kamera pandangan sekeliling, penderia lidar dan penderia radar gelombang milimeter untuk mengumpul maklumat dalam modaliti yang berbeza untuk mencapai tugas persepsi yang tepat. Algoritma persepsi BEV berdasarkan penglihatan tulen digemari oleh industri kerana kos perkakasannya yang rendah dan penggunaan mudah, dan hasil keluarannya boleh digunakan dengan mudah untuk pelbagai tugas hiliran.
 Penjelasan terperinci tentang mendapatkan hak pentadbir dalam Win11
Mar 08, 2024 pm 03:06 PM
Penjelasan terperinci tentang mendapatkan hak pentadbir dalam Win11
Mar 08, 2024 pm 03:06 PM
Sistem pengendalian Windows ialah salah satu sistem pengendalian yang paling popular di dunia, dan versi baharunya Win11 telah menarik perhatian ramai. Dalam sistem Win11, mendapatkan hak pentadbir adalah operasi penting Hak pentadbir membolehkan pengguna melakukan lebih banyak operasi dan tetapan pada sistem. Artikel ini akan memperkenalkan secara terperinci cara mendapatkan kebenaran pentadbir dalam sistem Win11 dan cara mengurus kebenaran dengan berkesan. Dalam sistem Win11, hak pentadbir dibahagikan kepada dua jenis: pentadbir tempatan dan pentadbir domain. Pentadbir tempatan mempunyai hak pentadbiran penuh ke atas komputer tempatan
 Melaksanakan Algoritma Pembelajaran Mesin dalam C++: Cabaran dan Penyelesaian Biasa
Jun 03, 2024 pm 01:25 PM
Melaksanakan Algoritma Pembelajaran Mesin dalam C++: Cabaran dan Penyelesaian Biasa
Jun 03, 2024 pm 01:25 PM
Cabaran biasa yang dihadapi oleh algoritma pembelajaran mesin dalam C++ termasuk pengurusan memori, multi-threading, pengoptimuman prestasi dan kebolehselenggaraan. Penyelesaian termasuk menggunakan penunjuk pintar, perpustakaan benang moden, arahan SIMD dan perpustakaan pihak ketiga, serta mengikuti garis panduan gaya pengekodan dan menggunakan alat automasi. Kes praktikal menunjukkan cara menggunakan perpustakaan Eigen untuk melaksanakan algoritma regresi linear, mengurus memori dengan berkesan dan menggunakan operasi matriks berprestasi tinggi.
 Penjelasan terperinci tentang operasi bahagian dalam Oracle SQL
Mar 10, 2024 am 09:51 AM
Penjelasan terperinci tentang operasi bahagian dalam Oracle SQL
Mar 10, 2024 am 09:51 AM
Penjelasan terperinci tentang operasi bahagi dalam OracleSQL Dalam OracleSQL, operasi bahagi ialah operasi matematik yang biasa dan penting, digunakan untuk mengira hasil pembahagian dua nombor. Bahagian sering digunakan dalam pertanyaan pangkalan data, jadi memahami operasi bahagian dan penggunaannya dalam OracleSQL adalah salah satu kemahiran penting untuk pembangun pangkalan data. Artikel ini akan membincangkan pengetahuan berkaitan operasi bahagian dalam OracleSQL secara terperinci dan menyediakan contoh kod khusus untuk rujukan pembaca. 1. Operasi bahagian dalam OracleSQL
 Terokai prinsip asas dan pemilihan algoritma bagi fungsi isihan C++
Apr 02, 2024 pm 05:36 PM
Terokai prinsip asas dan pemilihan algoritma bagi fungsi isihan C++
Apr 02, 2024 pm 05:36 PM
Lapisan bawah fungsi C++ sort menggunakan isihan gabungan, kerumitannya ialah O(nlogn), dan menyediakan pilihan algoritma pengisihan yang berbeza, termasuk isihan pantas, isihan timbunan dan isihan stabil.
 Bolehkah kecerdasan buatan meramalkan jenayah? Terokai keupayaan CrimeGPT
Mar 22, 2024 pm 10:10 PM
Bolehkah kecerdasan buatan meramalkan jenayah? Terokai keupayaan CrimeGPT
Mar 22, 2024 pm 10:10 PM
Konvergensi kecerdasan buatan (AI) dan penguatkuasaan undang-undang membuka kemungkinan baharu untuk pencegahan dan pengesanan jenayah. Keupayaan ramalan kecerdasan buatan digunakan secara meluas dalam sistem seperti CrimeGPT (Teknologi Ramalan Jenayah) untuk meramal aktiviti jenayah. Artikel ini meneroka potensi kecerdasan buatan dalam ramalan jenayah, aplikasi semasanya, cabaran yang dihadapinya dan kemungkinan implikasi etika teknologi tersebut. Kecerdasan Buatan dan Ramalan Jenayah: Asas CrimeGPT menggunakan algoritma pembelajaran mesin untuk menganalisis set data yang besar, mengenal pasti corak yang boleh meramalkan di mana dan bila jenayah mungkin berlaku. Set data ini termasuk statistik jenayah sejarah, maklumat demografi, penunjuk ekonomi, corak cuaca dan banyak lagi. Dengan mengenal pasti trend yang mungkin terlepas oleh penganalisis manusia, kecerdasan buatan boleh memperkasakan agensi penguatkuasaan undang-undang
 Algoritma pengesanan yang dipertingkatkan: untuk pengesanan sasaran dalam imej penderiaan jauh optik resolusi tinggi
Jun 06, 2024 pm 12:33 PM
Algoritma pengesanan yang dipertingkatkan: untuk pengesanan sasaran dalam imej penderiaan jauh optik resolusi tinggi
Jun 06, 2024 pm 12:33 PM
01Garis prospek Pada masa ini, sukar untuk mencapai keseimbangan yang sesuai antara kecekapan pengesanan dan hasil pengesanan. Kami telah membangunkan algoritma YOLOv5 yang dipertingkatkan untuk pengesanan sasaran dalam imej penderiaan jauh optik resolusi tinggi, menggunakan piramid ciri berbilang lapisan, strategi kepala pengesanan berbilang dan modul perhatian hibrid untuk meningkatkan kesan rangkaian pengesanan sasaran dalam imej penderiaan jauh optik. Menurut set data SIMD, peta algoritma baharu adalah 2.2% lebih baik daripada YOLOv5 dan 8.48% lebih baik daripada YOLOX, mencapai keseimbangan yang lebih baik antara hasil pengesanan dan kelajuan. 02 Latar Belakang & Motivasi Dengan perkembangan pesat teknologi penderiaan jauh, imej penderiaan jauh optik resolusi tinggi telah digunakan untuk menggambarkan banyak objek di permukaan bumi, termasuk pesawat, kereta, bangunan, dll. Pengesanan objek dalam tafsiran imej penderiaan jauh
 Penjelasan terperinci tentang peranan dan penggunaan pengendali modulo PHP
Mar 19, 2024 pm 04:33 PM
Penjelasan terperinci tentang peranan dan penggunaan pengendali modulo PHP
Mar 19, 2024 pm 04:33 PM
Operator modulo (%) dalam PHP digunakan untuk mendapatkan baki pembahagian dua nombor. Dalam artikel ini, kami akan membincangkan peranan dan penggunaan pengendali modulo secara terperinci, dan memberikan contoh kod khusus untuk membantu pembaca memahami dengan lebih baik. 1. Peranan pengendali modulo Dalam matematik, apabila kita membahagi integer dengan integer lain, kita mendapat hasil bagi dan baki. Sebagai contoh, apabila kita membahagi 10 dengan 3, hasil bahagi ialah 3 dan selebihnya ialah 1. Operator modulo digunakan untuk mendapatkan baki ini. 2. Penggunaan operator modulo Dalam PHP, gunakan simbol % untuk mewakili modulus




