详解分类评价指标和回归评价指标以及Python代码实现

这篇文章介绍的内容是详解分类评价指标和回归评价指标以及Python代码实现，有着一定的参考价值，现在分享给大家，有需要的朋友可以参考一下。

1、概念

性能度量（评价）指标，主分为两大类：
 1）分类评价指标（classification），主要分析，离散的，整数的。其具体指标包括accuracy(准确率)，precision(精确率)，recall(召回率)，F值，P-R曲线，ROC曲线和AUC。
 2）回归评价指标（regression），主要分析整数和实数之间的关系。其具体指标包括可释方差得分(explianed_variance_score)，平均绝对误差MAE(mean_absolute_error)，均方误差MSE(mean-squared_error)，均方根差RMSE，交叉熵lloss(Log loss，cross-entropy loss)，R方值(确定系数，r2_score)。

1.1、前提

假设只有两类-正类（positive）和负类（negative），通常以关注的类为正类，其他类为负类（故多类问题亦可归纳为两类）
 混淆矩阵（Confusion matrix）如下

实际类别	预测类别
	正	负	总结
正	TP	FN	P(实际为正)
负	FP	TN	N(实际为负)

表中AB模式：第一个表示预测结果的对错，第二个表示预测的类别。如TP表示，True Positive，即正确的预测为正类；FN表示，False Negative，即错误的预测为了负类。

2、评价指标（性能度量）

2.1、分类评价指标

2.1.1 值指标-Accuracy、Precision、Recall、F值

度量	Accuracy(准确率)	Precision(精确率)	Recall(召回率)	F值
定义	正确分类的样本数与总样本数之比（预测为垃圾短信中真正的垃圾短信的比例）	判定为正例中真正正例数与判定为正例数之比（所有真的垃圾短信被分类求正确找出来的比例）	被正确判定为正例数与总正例数之比	准确率与召回率的调和平均F-score
表示	accuracy=	precision=	recall=	F - score =

1.precision也常称为查准率，recall称为查全率
 2.比较常用的是F1，

python3.6代码实现：

#调用sklearn库中的指标求解from sklearn import metricsfrom sklearn.metrics import precision_recall_curvefrom sklearn.metrics import average_precision_scorefrom sklearn.metrics import accuracy_score#给出分类结果y_pred = [0, 1, 0, 0]
y_true = [0, 1, 1, 1]
print("accuracy_score:", accuracy_score(y_true, y_pred))
print("precision_score:", metrics.precision_score(y_true, y_pred))
print("recall_score:", metrics.recall_score(y_true, y_pred))
print("f1_score:", metrics.f1_score(y_true, y_pred))
print("f0.5_score:", metrics.fbeta_score(y_true, y_pred, beta=0.5))
print("f2_score:", metrics.fbeta_score(y_true, y_pred, beta=2.0))

2.1.2 相关曲线-P-R曲线、ROC曲线及AUC值

1）P-R曲线
步骤：
1、从高到低将”score”值排序并依次作为阈值threshold；
2、对于每个阈值，”score”值大于或等于这个threshold的测试样本被认为正例，其他为负例。从而形成一组预测数。
eg.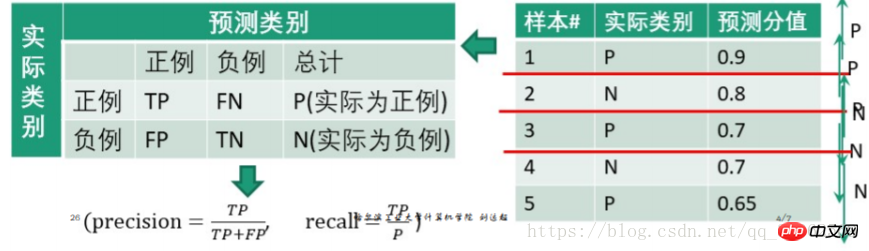

将0.9作为阈值，则第1个测试样本为正例，2、3、4、5为负例
得到

	预测为正例	预测为负例	总计
正例(score大于阈值)	0.9	0.1	1
负例(score小于阈值)	0.2+0.3+0.3+0.35 = 1.15	0.8+0.7+0.7+0.65 = 2.85	4
precision= recall=

在阈值以下的部分，当作负例，则预测为负例的取值情况是正确预测值，即如果本身是正例，则取TP；如果本身是负例，则取TN，其都为预测分值。
python实现伪代码

#precision和recall的求法如上
#主要介绍一下python画图的库
import matplotlib.pyplot ad plt
#主要用于矩阵运算的库
import numpy as np#导入iris数据及训练见前一博文
...
#加入800个噪声特征，增加图像的复杂度
#将150*800的噪声特征矩阵与150*4的鸢尾花数据集列合并
X = np.c_[X, np.random.RandomState(0).randn(n_samples, 200*n_features)]
#计算precision，recall得到数组
for i in range(n_classes):
    #计算三类鸢尾花的评价指标， _作为临时的名称使用
    precision[i], recall[i], _ = precision_recall_curve(y_test[:, i], y_score[:,i])#plot作图plt.clf()
for i in range(n_classes):
    plt.plot(recall[i], precision[i])
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel("Recall")
plt.ylabel("Precision")
plt.show()

将上述代码补充完整后得到鸢尾花数据集的P-R曲线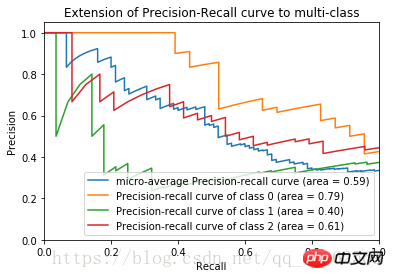

2）ROC曲线
横轴：假正例率 fp rate = FP / N
纵轴：真正例率 tp rate = TP / N
步骤：
1、从高到低将”score”值排序并依次作为阈值threshold；
2、对于每个阈值，”score”值大于或等于这个threshold的测试样本被认为正例，其他为负例。从而形成一组预测数。

同P-R曲线计算类似，不再赘述
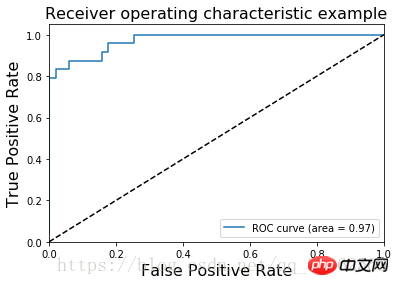
鸢尾花数据集的ROC图像为

AUC（Area Under Curve）定义为ROC曲线下的面积
AUC值提供了分类器的一个整体数值。通常AUC越大，分类器更好，取值为[0, 1]

2.2、回归评价指标

1）可释方差得分

2）平均绝对误差 MAE （Mean absolute error）

3）均方差 MSE （Mean squared error）


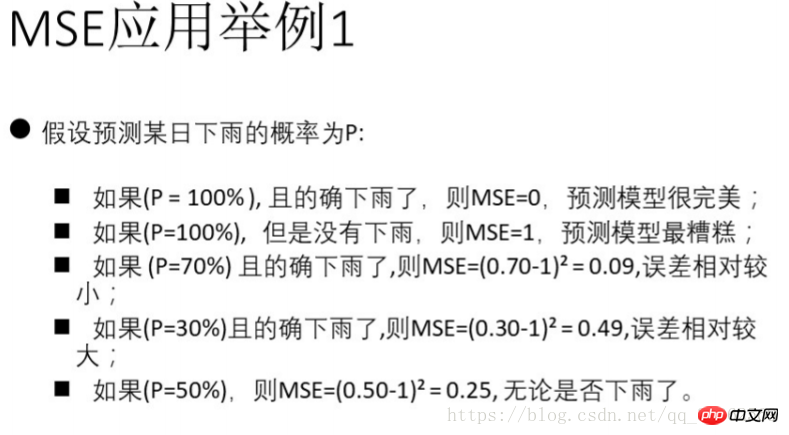
4）logistics回归损失

5）一致性评价 - pearson相关系数法

python代码实现

from sklearn.metrics import log_loss
log_loss(y_true, y_pred)from scipy.stats import pearsonr
pearsonr(rater1, rater2)from sklearn.metrics import cohen_kappa_score
cohen_kappa_score(rater1, rater2)

Atas ialah kandungan terperinci 详解分类评价指标和回归评价指标以及Python代码实现. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!