如何深入理解JavaScript中的递归
JavaScript中的递归就是指函数反复调用自己的过程,函数的调用是建立在堆栈中,在堆栈的顶部函数调用总是第一个弹出的。我们可以通过浏览器自带的开发工具来查看堆栈的调用
真正的理解JavaScript 中的递归是非常困难的,有的人甚至把它称为不必要的内存密集型和复杂版本的“for循环”。接下来将在文章中为大家详细介绍这个知识,希望对大家有所帮助。

【推荐课程:JavaScript教程】
编程中的递归是什么?
实质上, 递归是指函数或子例程反复调用自己的时候。所有递归函数调用都必须有一个基本情况。基本情况是让函数返回值而不是再次调用自身的特定条件。为了防止递归函数无限调用自身, 必须存在基本情况。如果省略或写入不正确, 就会出现错误。
不正确的基本情况指的是一个基本情况它不包括所有可能的用户输入, 这可能会导致因通过基本情况的特定输入而导致无休止的递归函数的调用, 从而导致调用堆栈溢出。
函数调用存储在调用堆栈上
函数的调用都是存储在堆栈中,调用堆栈是堆栈数据结构的特定实现。它是一个 LIFO (最后进入, 首先输出) 数据结构, 这就意味着放置在堆栈顶部的函数调用是第一个弹出的。
例:计算5的阶乘
<script>
function factorial(num) {
var nextNum = num - 1;
if (num === 1) {
return num;
}
return num * factorial(nextNum);
}
console.log(factorial(5));
</script>输出结果为:120
上述代码中,当解析到console.log(factorial(5));时,首先console.log()将被推送到堆栈上,之后factorial(5) 其结果将传递到console.log()函数中,当我们输入factorial(5)时, 调用堆栈将如下所示

语句return num * factorial(nextNum);表示阶乘函数返回num (本例中表示5) 乘以递归函数调用的返回值, 其中4被传入。实质上, 该函数返回以下值
return 5 * factorial(4);
因为factorial(4)是一个函数, 所以我们将把这个函数调用推送到调用堆栈上。现在我们将重复相同的过程, 直到我们到达基本情况 i. 当num等于1时。此时, 调用堆栈将如下所示。

一旦我们到达基本情况, 函数factorial(1)返回值1。因此现在我们知道factorial(1)等于 1, factorial(2) ) 也返回一个非函数值: 2 * factorial(1) , 即 2 * 1 = 2。
接着, factorial(3)返回3 * factorial(2), 等于6。等等, 直到我们得到factorial(5), 它返回 5 * 24 = 120。
如何查看调用堆栈
如果使用的是 chrome web 浏览器,可按 f12 (在 Windows 上), 打开chrome 开发人员工具。在顶部选项卡上, 您将看到菜单标签, 如元素、配置文件、控制台、网络、源等。单击"源"。如下所示
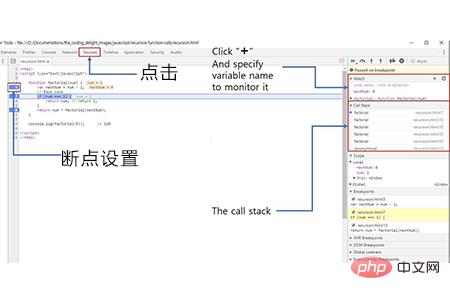
通过该开发工具可以直观地查看调用堆栈。当递归函数调用num === 1的条件时, 它将返回1。之后, 当函数调用返回时, 每个阶乘函数调用都将从堆栈中弹出。
总结:以上就是本篇文章的全部内容了,希望对大家有所帮助。
Atas ialah kandungan terperinci 如何深入理解JavaScript中的递归. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

Video Face Swap
Tukar muka dalam mana-mana video dengan mudah menggunakan alat tukar muka AI percuma kami!

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 Pelaksanaan rekursif fungsi C++: Adakah terdapat had untuk kedalaman rekursif?
Apr 23, 2024 am 09:30 AM
Pelaksanaan rekursif fungsi C++: Adakah terdapat had untuk kedalaman rekursif?
Apr 23, 2024 am 09:30 AM
Kedalaman rekursi fungsi C++ adalah terhad, dan melebihi had ini akan mengakibatkan ralat limpahan tindanan. Nilai had berbeza antara sistem dan penyusun, tetapi biasanya antara 1,000 dan 10,000. Penyelesaian termasuk: 1. Pengoptimuman rekursi ekor; 2. Panggilan ekor;
 Adakah ungkapan lambda C++ menyokong rekursi?
Apr 17, 2024 pm 09:06 PM
Adakah ungkapan lambda C++ menyokong rekursi?
Apr 17, 2024 pm 09:06 PM
Ya, ungkapan Lambda C++ boleh menyokong rekursi dengan menggunakan std::function: Gunakan std::function untuk menangkap rujukan kepada ungkapan Lambda. Dengan rujukan yang ditangkap, ungkapan Lambda boleh memanggil dirinya secara rekursif.
 Pelaksanaan rekursif fungsi C++: Analisis perbandingan algoritma rekursif dan bukan rekursif?
Apr 22, 2024 pm 03:18 PM
Pelaksanaan rekursif fungsi C++: Analisis perbandingan algoritma rekursif dan bukan rekursif?
Apr 22, 2024 pm 03:18 PM
Algoritma rekursif menyelesaikan masalah berstruktur melalui fungsi panggilan kendiri Kelebihannya ialah ia mudah dan mudah difahami, tetapi kelemahannya ialah ia kurang cekap dan boleh menyebabkan limpahan timbunan Algoritma bukan rekursif mengelakkan pengulangan dengan menguruskan secara eksplisit struktur data timbunan Kelebihannya ialah ia lebih cekap dan mengelakkan limpahan, kelemahannya ialah kod itu mungkin lebih kompleks. Pilihan rekursif atau bukan rekursif bergantung kepada masalah dan kekangan khusus pelaksanaan.
 Penalaan prestasi panggilan fungsi C++: kesan nilai lulus dan pulangan parameter
May 04, 2024 pm 12:57 PM
Penalaan prestasi panggilan fungsi C++: kesan nilai lulus dan pulangan parameter
May 04, 2024 pm 12:57 PM
Pengoptimuman prestasi panggilan fungsi C++ merangkumi dua aspek: strategi lulus parameter dan pengoptimuman jenis nilai pulangan. Dari segi lulus parameter, nilai lulus sesuai untuk objek kecil dan parameter tidak boleh diubah, manakala rujukan atau penunjuk lulus sesuai untuk objek besar dan parameter boleh diubah suai, dan penunjuk lulus adalah yang terpantas. Dari segi pengoptimuman nilai pulangan, nilai kecil boleh dikembalikan secara langsung, dan objek besar harus mengembalikan rujukan atau petunjuk. Memilih strategi yang sesuai boleh meningkatkan prestasi panggilan fungsi.
 Penjelasan terperinci tentang rekursi fungsi C++: aplikasi rekursi dalam pemprosesan rentetan
Apr 30, 2024 am 10:30 AM
Penjelasan terperinci tentang rekursi fungsi C++: aplikasi rekursi dalam pemprosesan rentetan
Apr 30, 2024 am 10:30 AM
Fungsi rekursif ialah teknik yang memanggil dirinya berulang kali untuk menyelesaikan masalah dalam pemprosesan rentetan. Ia memerlukan syarat penamatan untuk mengelakkan rekursi tak terhingga. Rekursi digunakan secara meluas dalam operasi seperti pembalikan rentetan dan pemeriksaan palindrom.
 C++ Recursion Advanced: Memahami Pengoptimuman Rekursi Ekor dan Aplikasinya
Apr 30, 2024 am 10:45 AM
C++ Recursion Advanced: Memahami Pengoptimuman Rekursi Ekor dan Aplikasinya
Apr 30, 2024 am 10:45 AM
Pengoptimuman rekursif ekor (TRO) meningkatkan kecekapan panggilan rekursif tertentu. Ia menukarkan panggilan rekursif ekor kepada arahan lompat dan menyimpan keadaan konteks dalam daftar dan bukannya pada tindanan, dengan itu menghapuskan panggilan tambahan dan operasi kembali kepada tindanan dan meningkatkan kecekapan algoritma. Menggunakan TRO, kita boleh mengoptimumkan fungsi rekursif ekor (seperti pengiraan faktorial dengan menggantikan panggilan rekursif ekor dengan pernyataan goto, pengkompil akan menukar lompatan goto kepada TRO dan mengoptimumkan pelaksanaan algoritma rekursif).
 Bagaimana untuk memanggil fungsi dalam modul yang berbeza dalam C++?
Apr 12, 2024 pm 03:54 PM
Bagaimana untuk memanggil fungsi dalam modul yang berbeza dalam C++?
Apr 12, 2024 pm 03:54 PM
Memanggil fungsi merentas modul dalam C++: Isytihar fungsi: Isytiharkan fungsi yang akan dipanggil dalam fail pengepala modul sasaran. Laksanakan fungsi: Laksanakan fungsi dalam fail sumber. Memautkan modul: Gunakan pemaut untuk memautkan bersama modul yang mengandungi pengisytiharan dan pelaksanaan fungsi. Panggil fungsi: Sertakan fail pengepala modul sasaran dalam modul yang perlu dipanggil, dan kemudian panggil fungsi tersebut.
 Penjelasan terperinci tentang rekursi fungsi C++: pengoptimuman rekursi ekor
May 03, 2024 pm 04:42 PM
Penjelasan terperinci tentang rekursi fungsi C++: pengoptimuman rekursi ekor
May 03, 2024 pm 04:42 PM
Definisi dan pengoptimuman rekursif: Rekursif: Fungsi memanggil dirinya sendiri secara dalaman untuk menyelesaikan masalah sukar yang boleh diuraikan kepada sub-masalah yang lebih kecil. Rekursi ekor: Fungsi melakukan semua pengiraan sebelum membuat panggilan rekursif, yang boleh dioptimumkan menjadi gelung. Keadaan pengoptimuman rekursif ekor: panggilan rekursif ialah operasi terakhir. Parameter panggilan rekursif adalah sama dengan parameter panggilan asal. Contoh praktikal: Kira faktorial: Fungsi tambahan factorial_helper melaksanakan pengoptimuman rekursi ekor, menghapuskan timbunan panggilan dan meningkatkan kecekapan. Kira nombor Fibonacci: Fungsi rekursif ekor fibonacci_helper menggunakan pengoptimuman untuk mengira nombor Fibonacci dengan cekap.






