必须懂的二叉树公式

1、一般二叉树的性质
性质1、在非空二叉树的i层上,至多有2^i个结点。
性质2、高度为K的二叉树中,最多有2^(k+1)-1个结点。
性质3、对于任何一棵非空的二叉树,如果叶结点的个数为n0,度为2的结点个数为n2,则有n0=n2+1。
2、完全二叉树
定义:如果一棵二叉树中,只有最下面的两层结点度数小于2,其余各层结点度数都等于2,并且最下面一层的结点,都集中在该层最左边的若干位置上,则此二叉树称为完全二叉树。
性质1、具有n个结点的完全二叉树的高度k为[log^2n]。
性质2、对于具有n个结点的完全二叉树,如果按照从上(根结点)到下(叶结点)和从左到右的顺序对二叉树中的所有结点从0开始到n-1进行编号,则对于任意的下标为i的结点,有:
(1)如果i=0,则它是根结点,它没有父结点;如果i>0,则它的父结点的下标为(i-1)/2。
(2)如果2i+1<=n-1,则下标为i的结点的左子结点的下标为2i+1;否则,下标为i的结点没有左子结点。
(3)如果2i+2<=n-1,则下标为i的结点的右子结点的下标为2i+2;否则,下标为i的结点没有右子结点。
3、满二叉树
定义:如果一棵二叉的任何结点或者是树叶,或有两棵非空子树,则此二叉树称作满二叉树。
性质、在满二叉树中,叶结点的个数比分支结点个数多1。
4、扩充二叉树
定义:扩充二叉树是对一个已有二叉树的扩充,扩充后原二叉树的结点都变为度数为2的分支结点。也是就是说,如果原结点的度数为2,则不变;度数为1,则增加一个分支;度数为0,则增加两个分支。
性质1、在扩充二叉树中,外部结点的个数比内部结点的个数多1。
性质2、对任意扩充二叉树,外部路径长度E和内部路径长度I之间满足以下关系:E=I+2n,其中n是内部结点个数。
更多常见问题的相关技术文章,请访问常见问题栏目进行学习!
Atas ialah kandungan terperinci 必须懂的二叉树公式. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1377
1377
 52
52
 Kaedah terperinci memasukkan carta alir kesan formula ke dalam PPT
Mar 26, 2024 pm 04:36 PM
Kaedah terperinci memasukkan carta alir kesan formula ke dalam PPT
Mar 26, 2024 pm 04:36 PM
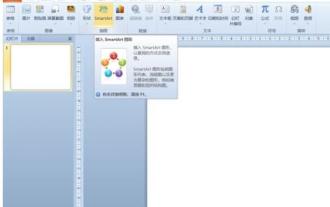
1. Buka PPT, klik tab [Sisipkan], dan klik butang [smartArt] dalam kumpulan [Ilustrasi]. 2. Klik [Proses] dalam kotak dialog [Select smartArt graphics] yang terbuka. 3. Pilih carta alir [Formula] dalam anak tetingkap [Proses] yang terbuka. 4. Klik [OK], dan carta alir [Formula] akan dimasukkan ke dalam anak tetingkap slaid. 5. Klik [Teks] dalam lajur [Type text here] atau klik [Teks] pada grafik untuk memasukkan kandungan. 6. Pilih bentuk dalam grafik, klik tab [Design] [Alat Seni Pintar] dan klik butang [Tambah Bentuk] dalam kumpulan [Buat Grafik] untuk menambah bentuk. 7. Bentuk dalam grafik juga boleh dipilih dan dipadam Sudah tentu, anda juga boleh memadamnya dalam smar seperti yang diperlukan.
 Bagaimana untuk mengendalikan formula jadual Excel
Mar 20, 2024 pm 12:07 PM
Bagaimana untuk mengendalikan formula jadual Excel
Mar 20, 2024 pm 12:07 PM
Apabila menggunakan perisian excel di tempat kerja, formula fungsi sering digunakan Jika anda ingin mahir menggunakan excel, anda mesti mahir dalam mengendalikan formula fungsi. Sebenarnya tidak sukar untuk menguasai formula Kita boleh mula belajar dari yang paling mudah Hari ini saya akan berkongsi dengan anda cara mengendalikan formula jadual Excel sebagai contoh, mari belajar bersama anda. 1. Pertama, buka excel Oleh kerana saya melakukan demonstrasi di sini, saya secara rawak memasukkan dua set data Sekarang kita perlu mengira hasil dua set data ini. Kami ingin mengira hasil darab lajur A dan B, dan meletakkan sel pada D4, seperti yang ditunjukkan dalam bulatan merah dalam rajah di bawah: 2. Kemudian, masukkan tanda sama dalam sel dan pilih sel parameter pertama B4, Masukkan tanda darab dan pilih parameter kedua C4
 Cetak paparan kiri pokok binari dalam bahasa C
Sep 03, 2023 pm 01:25 PM
Cetak paparan kiri pokok binari dalam bahasa C
Sep 03, 2023 pm 01:25 PM
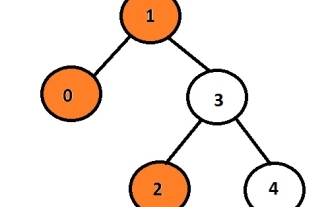
Tugasnya adalah untuk mencetak nod kiri pokok binari yang diberikan. Mula-mula, pengguna akan memasukkan data, dengan itu menjana pokok binari, dan kemudian mencetak pandangan kiri pokok yang terhasil. Setiap nod boleh mempunyai paling banyak 2 nod anak jadi atur cara ini mesti mengulangi hanya penunjuk kiri yang dikaitkan dengan nod jika penunjuk kiri tidak batal bermakna ia akan mempunyai beberapa data atau penunjuk yang dikaitkan dengannya jika tidak, ia akan dicetak dan dipaparkan sebagai anak kiri keluaran. ContohInput:10324Output:102Di sini, nod oren mewakili pandangan kiri pokok binari. Dalam graf yang diberikan, nod dengan data 1 adalah nod akar jadi ia akan dicetak dan bukannya pergi ke anak kiri ia akan mencetak 0 dan kemudian ia akan pergi ke 3 dan mencetak anak kirinya iaitu 2 . Kita boleh menggunakan kaedah rekursif untuk menyimpan tahap nod
 Penjelasan terperinci tentang struktur pokok binari di Jawa
Jun 16, 2023 am 08:58 AM
Penjelasan terperinci tentang struktur pokok binari di Jawa
Jun 16, 2023 am 08:58 AM
Pokok binari ialah struktur data biasa dalam sains komputer dan struktur data yang biasa digunakan dalam pengaturcaraan Java. Artikel ini akan memperkenalkan struktur pokok binari di Jawa secara terperinci. 1. Apakah pokok binari? Dalam sains komputer, pokok binari ialah struktur pokok di mana setiap nod mempunyai paling banyak dua nod anak. Antaranya, nod anak kiri lebih kecil daripada nod induk, dan nod anak kanan lebih besar daripada nod induk. Dalam pengaturcaraan Java, pokok binari biasanya digunakan untuk mewakili pengisihan, mencari dan meningkatkan kecekapan pertanyaan data. 2. Pelaksanaan pokok binari di Jawa Di Jawa, pokok binari
 Dalam bahasa C, cetak pandangan kanan pokok binari
Sep 16, 2023 pm 11:13 PM
Dalam bahasa C, cetak pandangan kanan pokok binari
Sep 16, 2023 pm 11:13 PM
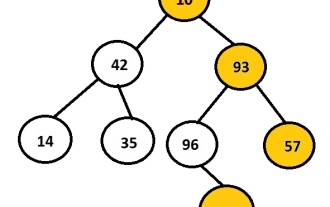
Tugasnya adalah untuk mencetak nod kanan pokok binari yang diberikan. Mula-mula pengguna akan memasukkan data untuk mencipta pokok binari dan kemudian mencetak pandangan kanan pokok yang terhasil. Imej di atas menunjukkan pepohon binari yang dicipta menggunakan nod 10, 42, 93, 14, 35, 96, 57 dan 88, dengan nod di sebelah kanan pepohon dipilih dan dipaparkan. Contohnya, 10, 93, 57, dan 88 ialah nod paling kanan bagi pokok binari. Contoh Input:1042931435965788Output:10935788 Setiap nod mempunyai dua penuding, penuding kiri dan penuding kanan. Menurut soalan ini, program hanya perlu melintasi nod yang betul. Oleh itu, anak kiri nod tidak perlu dipertimbangkan. Pandangan kanan menyimpan semua nod yang merupakan nod terakhir dalam hierarki mereka. Oleh itu, kita boleh
 Bagaimana untuk melaksanakan traversal pokok binari menggunakan Python
Jun 09, 2023 pm 09:12 PM
Bagaimana untuk melaksanakan traversal pokok binari menggunakan Python
Jun 09, 2023 pm 09:12 PM
Sebagai struktur data yang biasa digunakan, pokok binari sering digunakan untuk menyimpan data, mencari dan mengisih. Melintasi pokok binari adalah salah satu operasi yang sangat biasa. Sebagai bahasa pengaturcaraan yang mudah dan mudah digunakan, Python mempunyai banyak kaedah untuk melaksanakan traversal pokok binari. Artikel ini akan memperkenalkan cara menggunakan Python untuk melaksanakan traversal prapesanan, tertib dan pasca pesanan bagi pokok binari. Asas Pokok Binari Sebelum mempelajari cara melintasi pokok binari, kita perlu memahami konsep asas pokok binari. Pokok binari terdiri daripada nod, setiap nod mempunyai nilai dan dua nod anak (nod anak kiri dan nod anak kanan
 Cara menggunakan formula vlookup
Feb 19, 2024 pm 10:37 PM
Cara menggunakan formula vlookup
Feb 19, 2024 pm 10:37 PM
Formula VLOOKUP ialah fungsi yang sangat biasa digunakan dalam Microsoft Excel Ia digunakan untuk mencari nilai tertentu dalam jadual atau set data dan mengembalikan nilai lain yang dikaitkan dengannya. Dalam artikel ini, kita akan belajar cara menggunakan formula VLOOKUP dengan betul. Sintaks asas fungsi VLOOKUP adalah seperti berikut: VLOOKUP(lookup_value, table_array, col_index_num, [range_lookup]) di mana: lookup
 Bilangan segi tiga sama kaki dalam pokok binari
Sep 05, 2023 am 09:41 AM
Bilangan segi tiga sama kaki dalam pokok binari
Sep 05, 2023 am 09:41 AM
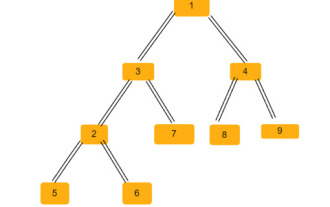
Pokok binari ialah struktur data di mana setiap nod boleh mempunyai sehingga dua nod anak. Kanak-kanak ini dipanggil anak kiri dan anak kanan masing-masing. Katakan kita diberi perwakilan tatasusunan induk, anda perlu menggunakannya untuk mencipta pokok binari. Pokok binari mungkin mempunyai beberapa segi tiga sama kaki. Kita perlu mencari jumlah bilangan segi tiga sama kaki yang mungkin dalam pokok binari ini. Dalam artikel ini, kami akan meneroka beberapa teknik untuk menyelesaikan masalah ini dalam C++. Memahami masalah memberi anda tatasusunan induk. Anda perlu mewakilinya dalam bentuk pokok binari supaya indeks tatasusunan membentuk nilai nod pokok dan nilai dalam tatasusunan memberikan nod induk indeks tertentu itu. Ambil perhatian bahawa -1 sentiasa menjadi induk akar. Diberikan di bawah adalah tatasusunan dan perwakilan pokok binarinya. Parentarray=[0,-1,3,1,



