递归算法的时间复杂度是什么

递归算法的时间复杂度是：【T(n)=o(f(n))】，它表示随问题规模n的增大，算法的执行时间增长率和f(n)增长率成正比，这称作算法的渐进时间复杂度。

递归算法的时间复杂度

时间复杂度： 

一般情况下，算法中基本操作重复的次数就是问题规模n的某个函数f（n），进而分析f（n）随n的变化情况并确定T（n）的数量级。这里用‘o’来表示数量级，给出算法时间复杂度。 

T（n）=o（f（n））； 

它表示随问题规模n的增大，算法的执行时间增长率和f（n）增长率成正比，这称作算法的渐进时间复杂度。而我们一般情况下讨论的最坏的时间复杂度。 

推荐课程：C语言教程

空间复杂度： 

算法的空间复杂度并不是实际占用的空间，而是计算整个算法空间辅助空间单元的个数，与问题的规模没有关系。算法的空间复杂度S（n）定义为该算法所耗费空间的数量级。 

S（n）=o（f（n）） 

若算法执行所需要的辅助空间相对于输入数据n而言是一个常数，则称这个算法空间复杂度辅助空间为o（1）； 

递归算法空间复杂度：递归深度n*每次递归所要的辅助空间，如果每次递归所需要的辅助空间为常数，则递归空间复杂度o（n）。

递归算法时间复杂度的计算方程式是一个递归方程：

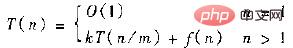
在引入递归树之前可以考虑一个例子：

T(n) = 2T(n/2) + n2

迭代2次可以得：

T(n) = n2 + 2(2T(n/4) + (n/2) 2)

还可以继续迭代，将其完全展开可得：

T(n) = n2 + 2((n/2) 2 +
2((n/22)2 + 2((n/23) 2 +
2((n/24) 2 +…+2((n/2i) 2 +
2T(n/2i + 1)))…))))……(1)

而当n/2i+1 == 1时，迭代结束。

将(1)式小括号展开，可得：

T(n) = n2 + 2(n/2)2 +
22(n/22) 2 + … + 2i(n/2i)2 +
2i+1T(n/2i+1)

这恰好是一个树形结构，由此可引出递归树法。

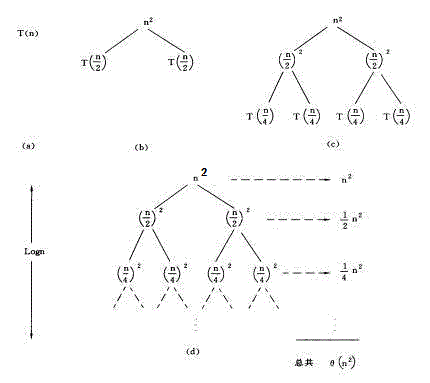
图中的(a)(b)(c)(d)分别是递归树生成的第1,2,3,n步。每一节点中都将当前的自由项n2留在其中，而将两个递归项T(n/2)
+ T(n/2)分别摊给了他的两个子节点，如此循环。

图中所有节点之和为:

[1 + 1/2 + (1/2)2 + (1/2)3 + … + (1/2)i] n2 = 2n2

可知其时间复杂度为O(n2)

可以得到递归树的规则为：

(1)每层的节点为T(n) = kT(n / m) + f(n)中的f(n)在当前的n/m下的值；

(2)每个节点的分支数为k；

(3)每层的右侧标出当前层中所有节点的和。

再举个例子：

T(n) = T(n/3) + T(2n/3) + n

其递归树如下图所示：

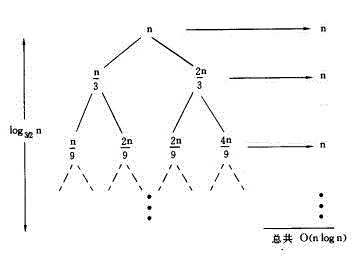
可见每层的值都为n，从根到叶节点的最长路径是：

因为最后递归的停止是在(2/3)kn == 1.则

于是　　

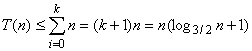
即T(n) = O(nlogn)　

总结，利用此方法解递归算法复杂度：

f(n) = af(n/b) + d(n)

1.当d(n)为常数时：

　　

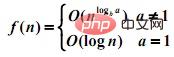
2.当d(n) = cn 时：

 

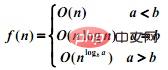
3.当d(n)为其他情况时可用递归树进行分析。

由第二种情况知，若采用分治法对原算法进行改进，则着重点是采用新的计算方法缩小a值。　　

Atas ialah kandungan terperinci 递归算法的时间复杂度是什么. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!