
Algoritma klasifikasi jiran atau K-nearest neighbor (kNN, k-NearestNeighbor) ialah salah satu kaedah paling mudah dalam teknologi pengelasan perlombongan data. Apa yang dipanggil K jiran terdekat bermaksud k jiran terdekat Ia bermakna setiap sampel boleh diwakili oleh k jiran terdekatnya.
Idea teras algoritma kNN ialah jika kebanyakan sampel bersebelahan k terdekat bagi sampel dalam ruang ciri tergolong dalam kategori tertentu, maka sampel itu juga tergolong dalam kategori ini dan mempunyai ciri sampel dalam kategori ini. Kaedah ini hanya menentukan kategori sampel yang hendak dikelaskan berdasarkan kategori satu atau beberapa sampel yang terdekat dalam menentukan keputusan pengelasan. Kaedah kNN hanya relevan kepada sebilangan kecil sampel bersebelahan apabila membuat keputusan kategori. Memandangkan kaedah kNN terutamanya bergantung pada sampel sekitar yang terhad dan bukannya kaedah mendiskriminasi domain kelas untuk menentukan kategori, kaedah kNN adalah lebih cekap daripada kaedah lain untuk set sampel yang akan dibahagikan yang mempunyai lebih banyak persilangan atau pertindihan dalam domain kelas. .
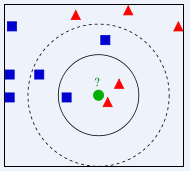
Dalam gambar di atas, bulatan hijau harus diberikan kepada kelas yang manakah ialah segi tiga merah atau segi empat sama biru? Jika K=3, kerana bahagian segi tiga merah ialah 2/3, bulatan hijau akan diberikan kelas bagi segi tiga merah Jika K=5, kerana bahagian segi empat biru ialah 3/5, bulatan hijau akan diberikan kelas jenis segi empat sama biru.
Algoritma klasifikasi K-Nearest Neighbor (KNN) ialah kaedah matang secara teori dan salah satu algoritma pembelajaran mesin yang paling mudah. Idea kaedah ini ialah: jika sampel tergolong dalam kategori tertentu antara sampel k yang paling serupa (iaitu, paling hampir dalam ruang ciri) dalam ruang ciri, maka sampel itu juga tergolong dalam kategori ini. Dalam algoritma KNN, jiran yang dipilih semuanya adalah objek yang dikelaskan dengan betul. Kaedah ini hanya menentukan kategori sampel yang akan dikelaskan berdasarkan kategori satu atau beberapa sampel yang terdekat dalam membuat keputusan pengelasan. Walaupun kaedah KNN juga bergantung pada teorem had pada dasarnya, ia hanya berkaitan dengan bilangan sampel bersebelahan yang sangat kecil apabila membuat keputusan kategori. Memandangkan kaedah KNN terutamanya bergantung pada sampel sekitar yang terhad dan bukannya kaedah mendiskriminasi domain kelas untuk menentukan kategori, kaedah KNN adalah lebih cekap daripada kaedah lain untuk set sampel dibahagikan dengan bilangan persimpangan atau pertindihan yang besar dalam domain kelas untuk kesesuaian.
Algoritma KNN boleh digunakan bukan sahaja untuk pengelasan, tetapi juga untuk regresi. Dengan mencari k jiran terdekat sampel dan memberikan purata sifat jiran ini kepada sampel, sifat sampel boleh diperolehi. Kaedah yang lebih berguna ialah memberikan pemberat yang berbeza kepada pengaruh jiran pada jarak yang berbeza pada sampel Contohnya, berat adalah berkadar songsang dengan jarak.
Gunakan algoritma kNN untuk meramalkan jantina pengguna filem Douban
Ringkasan
Artikel ini percaya bahawa jenis filem yang digemari oleh orang yang berlainan jantina adalah berbeza, jadi percubaan ini telah dijalankan. 100 filem baru-baru ini ditonton oleh 274 pengguna aktif Douban digunakan untuk membuat statistik tentang jenis mereka. 37 jenis filem yang diperoleh digunakan sebagai ciri atribut dan jantina pengguna digunakan sebagai label untuk membina set sampel. Gunakan algoritma kNN untuk membina pengelas jantina pengguna filem Douban, menggunakan 90% sampel sebagai sampel latihan dan 10% sebagai sampel ujian, dan ketepatan boleh mencapai 81.48%.
Data percubaan
Data yang digunakan dalam percubaan ini ialah filem yang ditandakan oleh pengguna Douban dan 100 filem baru-baru ini ditonton oleh 274 pengguna Douban telah dipilih. Statistik jenis filem untuk setiap pengguna. Terdapat sejumlah 37 jenis filem dalam data yang digunakan dalam percubaan ini, jadi 37 jenis ini digunakan sebagai ciri atribut pengguna, dan nilai setiap ciri ialah bilangan filem jenis itu dalam kalangan 100 filem pengguna. Pengguna dilabel mengikut jantina mereka Memandangkan Douban tidak mempunyai maklumat jantina pengguna, semuanya dilabel secara manual.
Format data adalah seperti berikut:
X1,1,X1,2,X1,3,X1,4……X1,36,X1,37,Y1 X2,1,X2,2,X2,3,X2,4……X2,36,X2,37,Y2 ………… X274,1,X274,2,X274,3,X274,4……X274,36,X274,37,Y274
Contoh:
0,0,0,3,1,34,5,0,0,0,11,31,0,0,38,40,0,0,15,8,3,9,14,2,3,0,4,1,1,15,0,0,1,13,0,0,1,1 0,1,0,2,2,24,8,0,0,0,10,37,0,0,44,34,0,0,3,0,4,10,15,5,3,0,0,7,2,13,0,0,2,12,0,0,0,0
像这样的数据一共有274行,表示274个样本。每一个的前37个数据是该样本的37个特征值,最后一个数据为标签,即性别:0表示男性,1表示女性。
在此次试验中取样本的前10%作为测试样本,其余作为训练样本。
首先对所有数据归一化。对矩阵中的每一列求取最大值(max_j)、最小值(min_j),对矩阵中的数据X_j,
X_j=(X_j-min_j)/(max_j-min_j) 。
然后对于每一条测试样本,计算其与所有训练样本的欧氏距离。测试样本i与训练样本j之间的距离为:
distance_i_j=sqrt((Xi,1-Xj,1)^2+(Xi,2-Xj,2)^2+……+(Xi,37-Xj,37)^2) ,
对样本i的所有距离从小到大排序,在前k个中选择出现次数最多的标签,即为样本i的预测值。
实验结果
首先选择一个合适的k值。 对于k=1,3,5,7,均使用同一个测试样本和训练样本,测试其正确率,结果如下表所示。
选取不同k值的正确率表
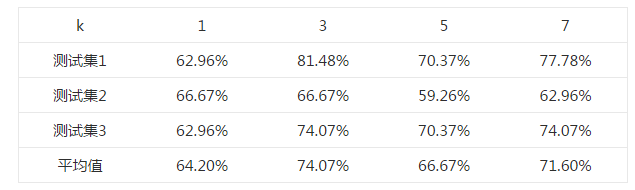
由上述结果可知,在k=3时,测试的平均正确率最高,为74.07%,最高可以达到81.48%。
上述不同的测试集均来自同一样本集中,为随机选取所得。
Python代码
这段代码并非原创,来自《机器学习实战》(Peter Harrington,2013),并有所改动。
#coding:utf-8
from numpy import *
import operator
def classify0(inX, dataSet, labels, k):
dataSetSize = dataSet.shape[0]
diffMat = tile(inX, (dataSetSize,1)) - dataSet
sqDiffMat = diffMat**2
sqDistances = sqDiffMat.sum(axis=1)
distances = sqDistances**0.5
sortedDistIndicies = distances.argsort()
classCount={}
for i in range(k):
voteIlabel = labels[sortedDistIndicies[i]]
classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1
sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)
return sortedClassCount[0][0]
def autoNorm(dataSet):
minVals = dataSet.min(0)
maxVals = dataSet.max(0)
ranges = maxVals - minVals
normDataSet = zeros(shape(dataSet))
m = dataSet.shape[0]
normDataSet = dataSet - tile(minVals, (m,1))
normDataSet = normDataSet/tile(ranges, (m,1)) #element wise divide
return normDataSet, ranges, minVals
def file2matrix(filename):
fr = open(filename)
numberOfLines = len(fr.readlines()) #get the number of lines in the file
returnMat = zeros((numberOfLines,37)) #prepare matrix to return
classLabelVector = [] #prepare labels return
fr = open(filename)
index = 0
for line in fr.readlines():
line = line.strip()
listFromLine = line.split(',')
returnMat[index,:] = listFromLine[0:37]
classLabelVector.append(int(listFromLine[-1]))
index += 1
fr.close()
return returnMat,classLabelVector
def genderClassTest():
hoRatio = 0.10 #hold out 10%
datingDataMat,datingLabels = file2matrix('doubanMovieDataSet.txt') #load data setfrom file
normMat,ranges,minVals=autoNorm(datingDataMat)
m = normMat.shape[0]
numTestVecs = int(m*hoRatio)
testMat=normMat[0:numTestVecs,:]
trainMat=normMat[numTestVecs:m,:]
trainLabels=datingLabels[numTestVecs:m]
k=3
errorCount = 0.0
for i in range(numTestVecs):
classifierResult = classify0(testMat[i,:],trainMat,trainLabels,k)
print "the classifier came back with: %d, the real answer is: %d" % (classifierResult, datingLabels[i])
if (classifierResult != datingLabels[i]):
errorCount += 1.0
print "Total errors:%d" %errorCount
print "The total accuracy rate is %f" %(1.0-errorCount/float(numTestVecs))




