java面试——数据结构

常见数据结构有：HashMap、Hashtable、 ConcurrentHashMap。

（相关视频分享：java教学视频）

下面我们分别来进行介绍：

HashMap

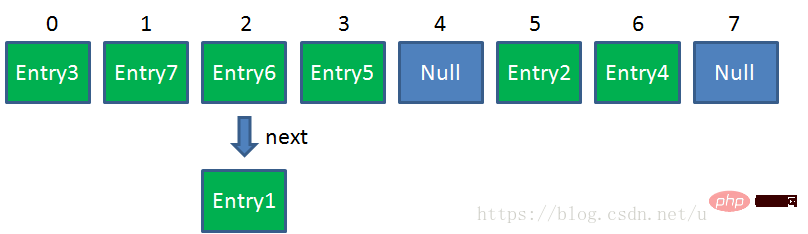
• 底层实现：HashMap底层整体结构是一个数组，数组中的每个元素又是一个链表。每次添加一个对象（put）时会产生一个链表对象（Object类型），Map中的每个Entry就是数组中的一个元素（Map.Entry就是一个<Key,Value>），它具有由当前元素指向下一个元素的引用，这就构成了链表。
• 存储原理：当向HsahMap中添加元素的时候，首先计算Key对象的Hash值，得到数组下标，如果数组该位置为空则插入，否则遍历这个位置链表。当某个节点Key对象和Node对象均和新元素的equals时，用新元素的Value对象替换该节点的Value对象，否则插入新节点。（注意：JDK 8之后加入了红黑树）

HashMap长度为2的n次幂是为了让length-1的二进制值所有位全为1，这种情况下，hash值与(table.length - 1)进行&运算计算index时，其结果就等同于hashcode后几位的值，此时只要输入的hashcode本身分布均匀，Hash算法的结果就是均匀的。所以，HashMap的默认长度为16是为了降低hash碰撞的几率，同时也是一种合适的大小。

Hashtable

比较点	HashMap	Hashtable
实现原理	见上小节	和HashMap的实现原理几乎一样
Key和Value	允许Key和Value为null	不允许Key和Value为null
扩容策略	2倍扩容oldThr << 1	2倍+1扩容(oldCapacity << 1) + 1
安全性	线程不安全	线程安全

Hashtable线程安全的策略实现代价很大，get/put所有相关操作都是synchronized的，在竞争激烈的并发场景中性能非常差。

ConcurrentHashMap

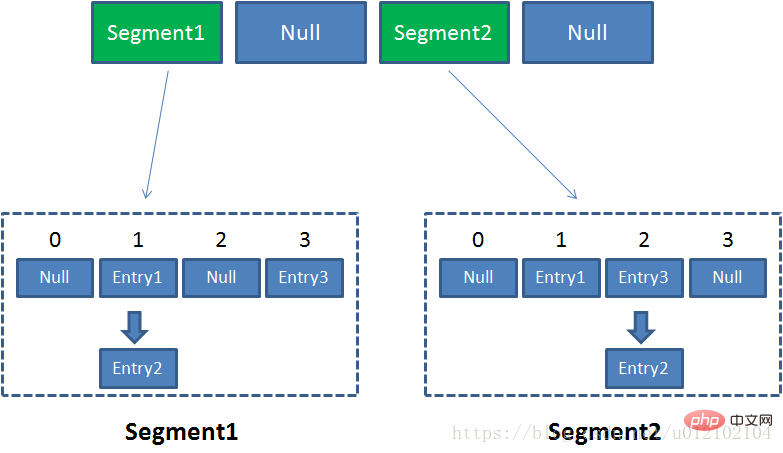
ConcurrentHashMap是Java并发包中提供的一个线程安全且高效的HashMap实现，它采用了非常精妙的分段锁策略，ConcurrentHashMap的主干是Segment数组。Segment继承于ReentrantLock，是一种可重入锁。每个Segment都是一个子哈希表，Segment里维护了一个HashEntry数组，并发环境下，对于不同Segment的数据进行操作不用考虑锁竞争。

LinkedHashMap、TreeMap、TreeSet

• LinkedHashMap：顺序存取的HashMap（基于数组和双向链表实现）。
• TreeMap：内部排序（基于红黑树实现）。
• TreeSet：有序的Set集合（基于二叉树实现）。

ArrayList、LinkedList、Vector

• ArrayList：动态数组（基于数组实现）。
• LinkedList：有序数组（基于双向链表实现）。
• Vector：对象容器，可放入不同类的对象（基于数组实现）。

Collection与Collections

• Collection：集合类的上级接口，子接口主要有List、Set 、Queue等。
• Collections：提供对集合进行搜索、排序、替换和线程安全化等操作的工具类。

（更多相关面试题推荐：java面试题及答案）

二叉树

常见二叉树概念

• B+树：见数据库部分https://blog.csdn.net/u012102104/article/details/79773362

• 平衡二叉树（AVL树）：各个结点左右子树深度差的绝对值不超过1。

• 哈夫曼树：带权路径长度最小的二叉树称为最优二叉树。哈夫曼树构造不唯一，但所有叶子结点的带权路径长度之和都是最小的。

• 红黑树：一种自平衡二叉查找树，它的性质有：

  1. 节点是红色或黑色。
  2. 根节点是黑色。
  3. 每个叶子节点都是黑色的空节点（NIL节点）。
  4. 每个红色节点的两个子节点都是黑色。
  5. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。

  从每个叶子到根的所有路径上不能有两个连续的红色节点

二叉树的遍历

// 1. 先序遍历算法 DLRvoid Preorder ( BinTree bt ) {
	if ( bt ) {
		visit ( bt->data );
		Preorder ( bt->lchild );
		Preorder ( bt->rchild );
	}}// 2. 中序遍历算法 LDRvoid Inorder ( BinTree bt ) {
	if ( bt ) {
		Inorder ( bt->lchild );
		visit ( bt->data );
		Inorder ( bt->rchild );
	}}// 3. 后序遍历 LRDvoid Postorder ( BinTree bt ) {
	if ( bt ) {
		Postorder ( bt->lchild );
		Postorder ( bt->rchild );
		visit ( bt->data );
	}}// 4. 按层次遍历。/* 思路：利用一个队列，首先将根（头指针）入队列，以后若队列不空则取队头元素 p，
如果 p 不空，则访问之，然后将其左右子树入队列，如此循环直到队列为空。*/void LevelOrder ( BinTree bt ) {
	// 队列初始化为空
	InitQueue ( Q );
	// 根入队列
	EnQueue ( Q, bt );
	// 队列不空则继续遍历
	while ( ! QueueEmpty(Q) ) {
		DeQueue ( Q, p );
		if ( p!=NULL ) {
			visit ( p->data );
			// 左、右子树入队列
			EnQueue ( Q, p->lchild );
			EnQueue ( Q, p->rchild );
		}
	}}// 非递归遍历二叉树一般借助栈实现
相关推荐：java入门教程





Atas ialah kandungan terperinci java面试——数据结构. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!