
Di kuil suci Benares (di utara India) di tengah dunia, terdapat tiga jarum permata yang dimasukkan pada pinggan tembaga. Apabila Brahma, tuhan utama agama Hindu, mencipta dunia, dia mengikat 64 keping emas dari besar ke kecil pada salah satu jarum dari bawah ke atas Ini adalah yang dipanggil Menara Hanoi. Tidak kira siang atau malam, sentiasa ada seorang sami yang menggerakkan kepingan emas ini mengikut peraturan berikut: hanya gerakkan satu keping pada satu masa, tidak kira jarum mana yang digunakan, kepingan kecil mesti berada di atas kepingan besar. Para bhikkhu meramalkan bahawa apabila semua kepingan emas dipindahkan dari jarum berulir oleh Brahma ke jarum lain, dunia akan dihapuskan dengan petir, dan Menara Vatican, kuil dan semua makhluk hidup juga akan binasa bersama.Terdapat banyak variasi lagenda ini dan tidak diketahui siapa dia, tetapi masalah matematik yang ditinggalkan adalah sangat klasik. Pengetahuan matematik yang ditinggalkan: hubungan antara bilangan keping emas dan bilangan langkah bergerak ialah
. 2^n - 1
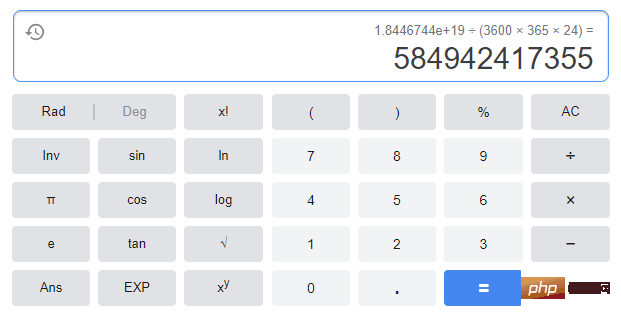
langkah untuk menyelesaikan tugas ini; dengan mengandaikan mereka memindahkan satu keping emas sesaat, ia akan mengambil masa 584.9 bilion tahun untuk diselesaikan. Seluruh alam ini hanya berusia 13.7 bilion tahun, jadi masih awal untuk kemusnahan alam semesta ... (Saya bosan, jadi saya benar-benar mengiranya, seperti yang ditunjukkan di bawah) 2^64 - 1
Peraturan asas
Algoritma Menara Hanoi mempunyai dua syarat asas, dengan mengandaikan bahawa plat dialihkan. 1. Hanya satu pinggan boleh dialihkan pada satu masa.2. Pinggan kecil mesti berada di atas pinggan besar.
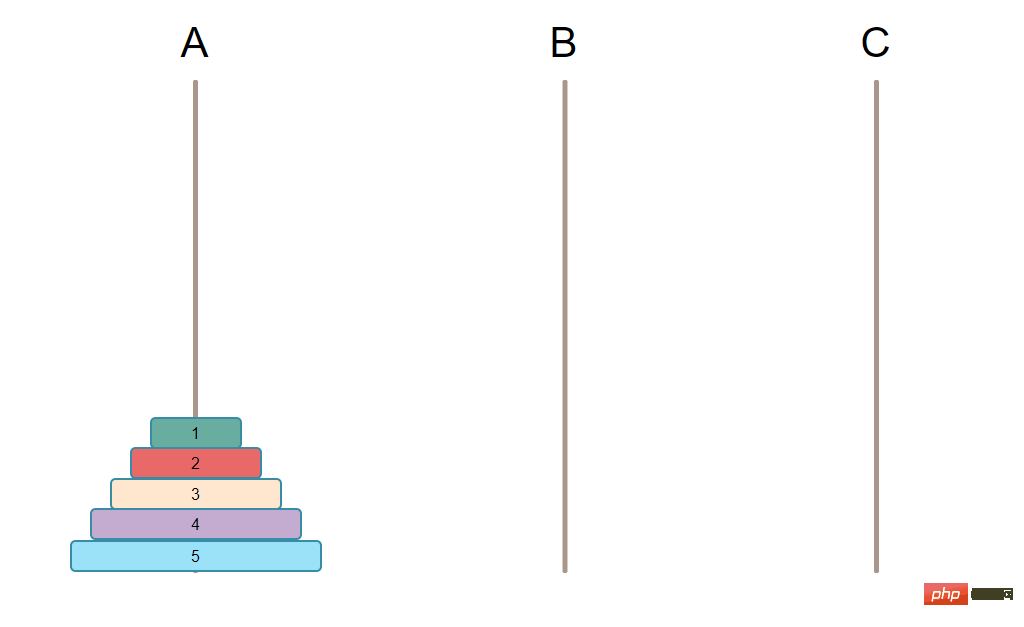
Tutorial video PHP]
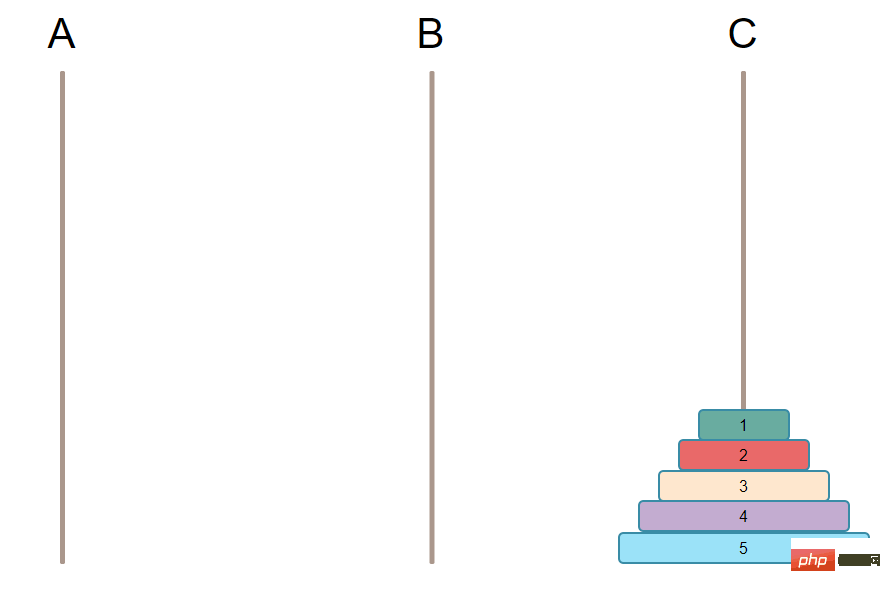
N-1
N-1 juga tertib pada tiang B. N-1
Langkah pertama ialah mengalihkan plat N-1 pada A ke B.
Kenapa alihkan N-1 ke B dahulu? Anda lihat, kerana apa yang akhirnya anda capai ialah memindahkan semua plat pada A ke C, susunannya tidak boleh diubah, hanya boleh yang besar berada di bahagian bawah dan yang kecil berada di atas. Kemudian anda pasti perlu memindahkan yang terbesar ke C terlebih dahulu, jika tidak, syarat tidak akan dipenuhi. Untuk mengalihkan plat terbesar dari A ke C, plat terbesar di A mesti dikosongkan, iaitu semua plat pada plat terbesar mesti dialihkan. Dan anda hanya mempunyai 3 tiang mesti tiada pemegang plat lain pada C, jika tidak, anda tidak akan memenuhi syarat Semua plat N-1 hanya boleh diletakkan di B, dan ia masih teratur. Ia menjadi gambar berikut: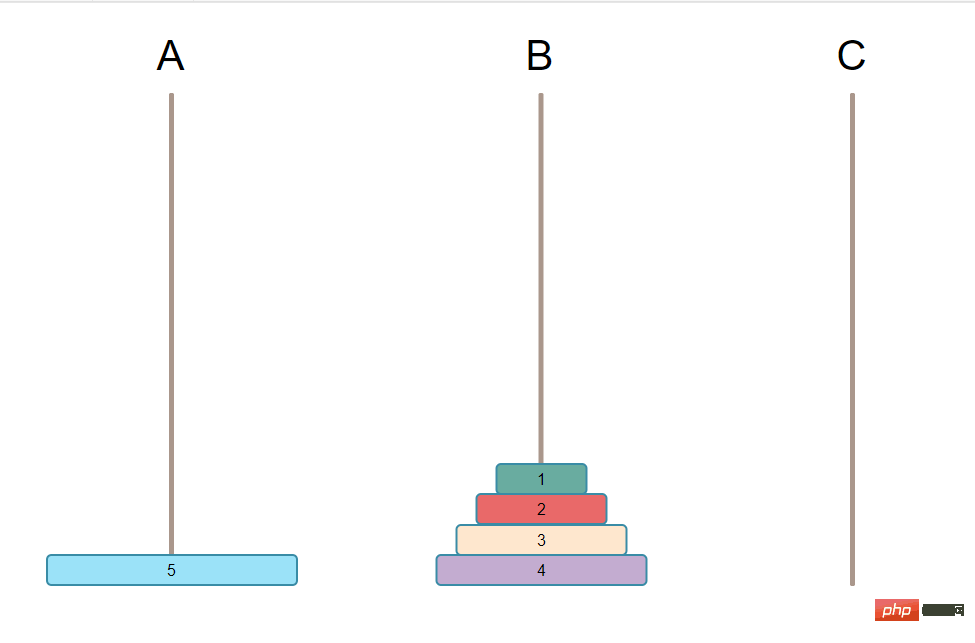
Langkah kedua ialah mengalihkan plat N pada A (iaitu plat terbesar) ke C.
Ini sangat mudah. Hanya alihkan plat terbesar dari A ke C dalam satu langkah. Seperti yang ditunjukkan di bawah:
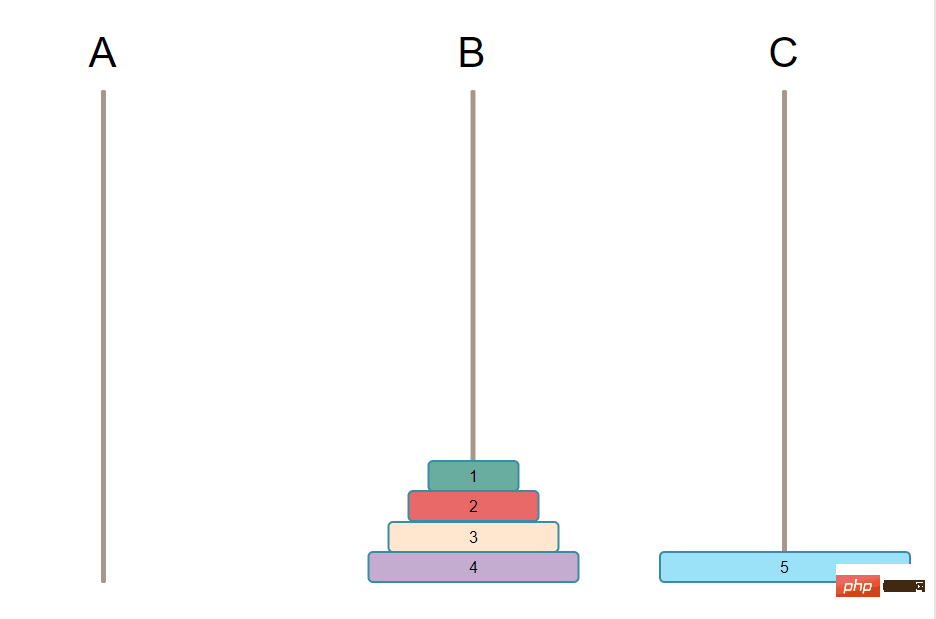
Langkah ketiga ialah mengalihkan plat N-1 pada B ke C.
Nota: Untuk mengalihkan plat N-1 ke C, adakah ia bertukar menjadi mencari plat terbesar di antara mereka, dan kemudian mengalihkan plat terbesar terlebih dahulu. Jadi di sini ia sebenarnya menjadi masalah untuk mengulangi langkah 1 dan 2, mencari yang terbesar di antara N-1 ini dan mengalihkannya ke C terlebih dahulu, dan kitaran berulang.
Langkah ketiga sebenarnya bersamaan dengan menukar keperluan.
Terdapat plat K pada tiang B, tiang A kosong, dan tiang C mempunyai plat terbesar, jadi untuk tiang B dengan plat K, ia bersamaan dengan kosong.
Langkah pertama ialah mengalihkan plat K-1 pada B ke A.
Langkah kedua ialah mengalihkan plat Kth pada B ke C.
Langkah ketiga ialah mengalihkan plat K-1 pada A ke C.
…
menjadi gambar di bawah
Mula-mula cari yang terbesar antara plat yang tinggal
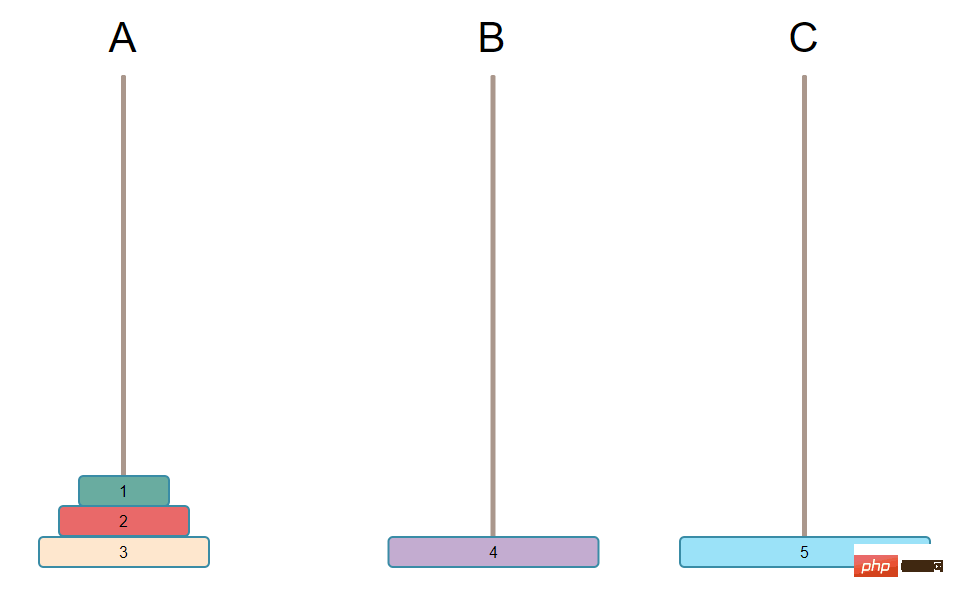
dan kemudian gerakkan plat terbesar
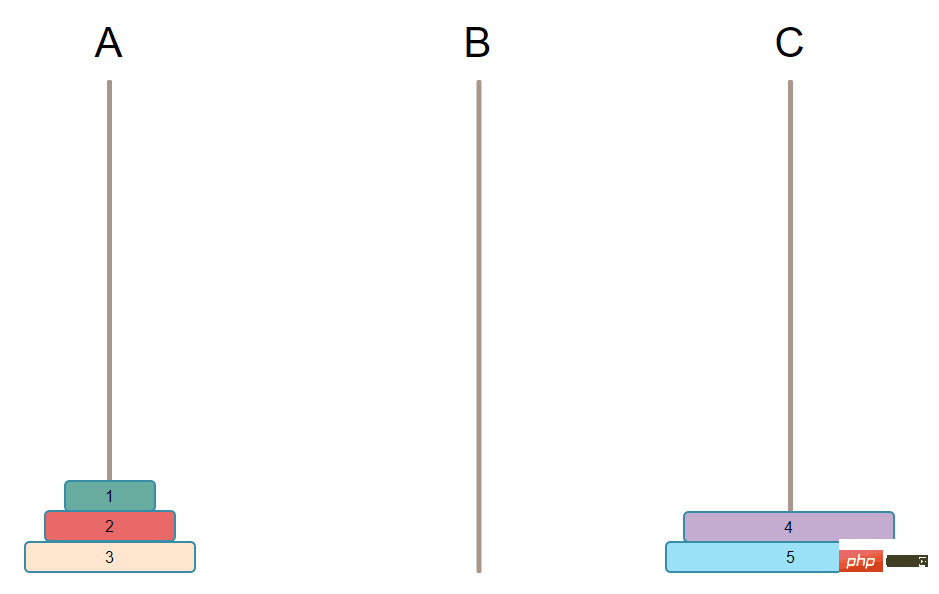
Kemudian gelung sehingga hanya tinggal satu pinggan, bergerak terus ke C, dan permainan tamat.
Apakah itu tiang bantu? Andaikan bahawa semua plat yang anda ingin alihkan berada pada A, dan matlamatnya adalah untuk bergerak ke C, maka B ialah tiang tambahan bagi plat N-1. Kerana mereka hanya boleh wujud di sini buat sementara waktu, jika tidak, mereka tidak akan memenuhi peraturan permainan.
Di sini anda perlu mencari tiang tambahan terlebih dahulu. Jangan fikirkan cara untuk melaksanakannya, tetapi jelaskan logiknya terlebih dahulu.
Daripada analisis di atas, kita dapat melihat bahawa ini sebenarnya adalah operasi berulang, yang sangat berulang. Sama seperti rekursi, semuanya di sini boleh dilaksanakan menggunakan rekursi.
Untuk menggunakan rekursi, terdapat 2 syarat yang diperlukan
1 Cari formula rekursi
2. Cari keadaan keluar
Keadaan keluar Ia mudah untuk menulis. Ia mesti dipindahkan terus ke tiang C apabila hanya ada satu pinggan.
Jadi apakah formula rekursi? Berdasarkan analisis logik di atas, ia boleh diuraikan kepada 3 langkah.
Langkah pertama ialah mengalihkan plat [N-1] dari A ke B
Langkah kedua ialah mengalihkan plat [N-1] dari A ke C
Langkah ketiga ialah mengalihkan [baki N-1] plat dari B ke C
Berikut ialah kod pseudo yang dilaksanakan dalam PHP:
class HanoiTower
{
// 计数器
public $count = 0;
/**
* 汉诺塔实现
*
* @param $n 盘子号
* @param $A 初始柱子
* @param $B 中转站
* @param $C 目标柱子
*/
public function hanoi($n, $A, $B, $C)
{
if ($n == 1) {
// 退出条件 只剩一个盘子的时候直接从A移动到C
$this->biggestOne($n, $A, $B, $C);
} else {
// Analisis bagaimana PHP melaksanakan algoritma Menara Hanoi yang menarik把 【n-1】 个盘子从A移动到B 此时C为中转站
$this->hanoi($n - 1, $A, $C, $B);
// Analisis bagaimana PHP melaksanakan algoritma Menara Hanoi yang menarik把 【第n】 个盘子从A移动到C
$this->biggestOne($n, $A, $B, $C);
// 第三步把B上 【剩余的n-1个】 盘子从B移动到C 此时A为中转站
$this->hanoi($n - 1, $B, $A, $C);
}
}
/**
* 移动最大的盘子
* 直接从A移动到C
*/
public function biggestOne($n, $A, $B, $C)
{
++$this->count;
echo '第', $this->count, '步 ', '把 ', $n, '从 ', $A, '移动到', $C, '<br />';
}
}
$n = 5;
$hanoiTower = new HanoiTower();
echo '这是一个有 【', $n, '】 个盘子的汉诺塔:', '<br />';
// 调用执行
$hanoiTower->hanoi($n, 'A', 'B', 'C');
echo '总共需要走:【', $hanoiTower->count, '】 步';Keputusannya adalah seperti berikut:
 >
>
Atas ialah kandungan terperinci Analisis bagaimana PHP melaksanakan algoritma Menara Hanoi yang menarik. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
 Bagaimana untuk membuka fail php
Bagaimana untuk membuka fail php
 Bagaimana untuk mengalih keluar beberapa elemen pertama tatasusunan dalam php
Bagaimana untuk mengalih keluar beberapa elemen pertama tatasusunan dalam php
 Apa yang perlu dilakukan jika penyahserialisasian php gagal
Apa yang perlu dilakukan jika penyahserialisasian php gagal
 Bagaimana untuk menyambungkan php ke pangkalan data mssql
Bagaimana untuk menyambungkan php ke pangkalan data mssql
 Bagaimana untuk menyambung php ke pangkalan data mssql
Bagaimana untuk menyambung php ke pangkalan data mssql
 Bagaimana untuk memuat naik html
Bagaimana untuk memuat naik html
 Bagaimana untuk menyelesaikan aksara bercelaru dalam PHP
Bagaimana untuk menyelesaikan aksara bercelaru dalam PHP
 Bagaimana untuk membuka fail php pada telefon bimbit
Bagaimana untuk membuka fail php pada telefon bimbit