
Dalam medan komputer, [folder] yang kami uruskan setiap hari dan data yang kami simpan dalam pangkalan data adalah semua aplikasi tipikal pokok. Hari ini kita akan belajar tentang definisi yang lebih teoritis bagi pokok dan pokok binari serta beberapa sifat dan cirinya.

Daripada contoh di atas dalam kehidupan sebenar, kita dapat melihat bahawa struktur pokok boleh meringkaskan beberapa cirinya.
Pokok ialah set terhingga nod N (N>0) Ia sama ada pokok kosong (N=0) atau pokok tidak kosong T.
Dalam definisi ini, kita perlu menjelaskan dua isu: Pertama, pokok mesti mempunyai nod, dan kedua, mengikut bilangan nod, ia boleh dibahagikan kepada dua jenis: pokok kosong dan pokok tidak kosong . Tetapi ini hanyalah definisi paling asas, ia mempunyai beberapa sifat.
Hanya terdapat satu nod yang dipanggil akar.
Dengan kata lain, pokok ini mesti mengembang dari nod tertentu, iaitu seperti akar pokok. Darinya mula bercabang ke luar.
Kecuali nod akar, nod yang selebihnya boleh dibahagikan kepada m ( m > 0 ) set terhingga terputus T1, T2..., Tm, setiap satunya ialah pokok sendiri, dan Subtree dipanggil akar (SubTree)
Perenggan ini mungkin tidak mudah difahami Sebenarnya, secara terang-terangan, setiap nod hanya mempunyai satu nod unggul dan tidak boleh mempunyai berbilang nod superior. Dengan cara yang sama, tidak boleh ada sebarang sambungan antara nod mendatar, tetapi ia boleh mempunyai berbilang nod bawahan.
Mengenai definisi pokok, kita boleh lihat gambar di bawah.
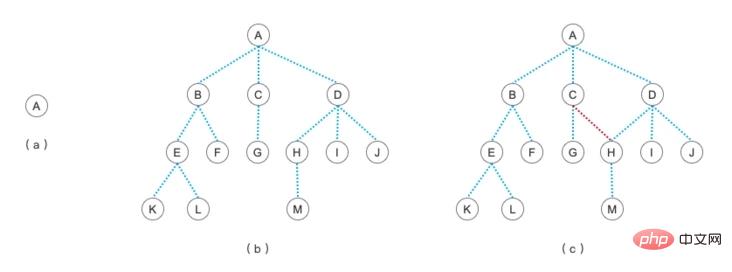
Gambar di atas hanya menyenaraikan rupa pokok standard dan bukan pokok standard. Antaranya:
(a) ialah pokok dengan hanya satu nod akar Selagi ada satu nod, ia boleh dipanggil struktur pokok
Secara umumnya, bentuk pokok boleh berubah-ubah Contohnya, satu nod mungkin mempunyai 3 nod anak, manakala nod lain mungkin mempunyai 300 nod anak. Pokok sedemikian tanpa sebarang peraturan sebenarnya akan menjadi sangat menyusahkan untuk dikendalikan, dan definisi pokok binari adalah lebih mudah Selain sifat pokok, ia juga mempunyai satu lagi kandungan: setiap nod pokok binari mempunyai paling banyak dua nod anak, iaitu, darjah keseluruhan pokok binari mestilah 2, dan darjah semua nod tidak akan melebihi 2. Mengenai mengapa pokok binari mudah dikendalikan, kami akan menerangkan secara terperinci sifat-sifat pokok binari dalam bahagian seterusnya. Semua struktur pokok boleh ditukar menjadi pokok binari melalui ubah bentuk biasa tertentu.
Kami juga menggunakan gambar rajah untuk menunjukkan apa itu pokok binari.
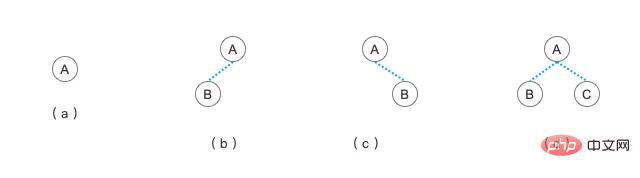
Dalam pokok binari, nod anak kiri dan keturunannya boleh dianggap sebagai subpokok kiri nod semasa. Nod kanan dan nod turunannya juga boleh dianggap sebagai subpokok kanan nod semasa. Menurut nod anak nod, terdapat beberapa bentuk pokok binari seperti yang ditunjukkan dalam rajah di atas.
(a) Pokok ialah pokok dengan hanya satu nod Ia juga boleh dikatakan sebagai pokok binari dengan hanya satu nod
(b ) Pokok itu ialah pokok binari dengan hanya satu nod kiri
(c) Pokok itu ialah pokok binari dengan hanya satu nod kanan
(d ) pokok ialah pokok binari dengan dua nod kiri dan kanan
Harta 1: Pada aras ke-i pokok binari Terdapat paling banyak 2i-1 nod (i >= 1)
Sifat 2: Pokok binari dengan kedalaman k mempunyai paling banyak 2k - 1 nod ( k >= 1)
Sifat 3: Untuk mana-mana pokok binari T, jika bilangan nod terminal ialah n0 dan bilangan nod dengan darjah 2 ialah n2, maka n0 = n2 1
Sifat 4: Pokok binari lengkap dengan n nod Kedalaman ialah log2n 1
Sifat 5: Jika nod pokok binari lengkap dengan n nod (kedalamannya ialah log2n 1) dinomborkan dalam susunan lapisan (daripada peringkat 1 ke peringkat log2n 1 , setiap lapisan dari kiri ke kanan), kemudian untuk mana-mana nod i (1
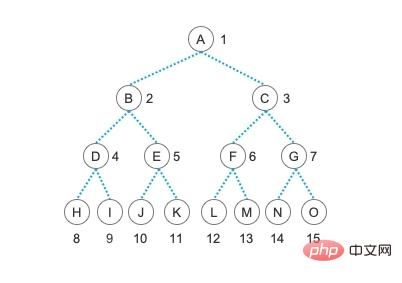
Akhir sekali, mari kita fahami secara ringkas apa itu "hutan". Pelbagai pokok disatukan membentuk "hutan". Sama seperti gambarajah penjelasan pokok binari di atas, (a) (b) (c) (d) disatukan dan dilihat secara keseluruhan, ia adalah "hutan", dan dalam "hutan" ini terdapat (a) (b) (c) (d) empat pokok ini.
Tiada kaitan antara pokok-pokok di dalam hutan Jika kita ingin beroperasi atau meredah hutan, kita sering menukar hutan menjadi pokok. Algoritma dan langkah khusus bukanlah fokus kajian kami, jadi semua orang boleh memahaminya. Pelajar yang ingin belajar secara mendalam boleh mencari kandungan yang berkaitan atau merujuk buku teks yang berkaitan.
Dari susunan dan barisan ke belakang pokok, adakah anda tiba-tiba merasakan bahawa anda telah mengambil langkah besar? Sedikit keliru? Tidak mengapa, kandungan hari ini sebenarnya adalah beberapa kandungan teori yang asas Jika anda boleh memahaminya, fahaminya.
Pembelajaran tidak melibatkan pengulangan proses kemajuan Sudah tentu, semuanya mesti berdasarkan asas. Selepas anda memahami struktur data pokok dan beberapa algoritma traversal yang mudah, kembali untuk memahami konsep ini secara mendalam dan menghafalnya.
Pembelajaran yang disyorkan: tutorial video php
Atas ialah kandungan terperinci Ketahui tentang pokok dan pokok binari dalam masa tiga minit. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
 Bagaimana untuk membuka fail php
Bagaimana untuk membuka fail php
 Bagaimana untuk mengalih keluar beberapa elemen pertama tatasusunan dalam php
Bagaimana untuk mengalih keluar beberapa elemen pertama tatasusunan dalam php
 Apa yang perlu dilakukan jika penyahserialisasian php gagal
Apa yang perlu dilakukan jika penyahserialisasian php gagal
 Bagaimana untuk menyambungkan php ke pangkalan data mssql
Bagaimana untuk menyambungkan php ke pangkalan data mssql
 Bagaimana untuk menyambung php ke pangkalan data mssql
Bagaimana untuk menyambung php ke pangkalan data mssql
 Bagaimana untuk memuat naik html
Bagaimana untuk memuat naik html
 Bagaimana untuk menyelesaikan aksara bercelaru dalam PHP
Bagaimana untuk menyelesaikan aksara bercelaru dalam PHP
 Bagaimana untuk membuka fail php pada telefon bimbit
Bagaimana untuk membuka fail php pada telefon bimbit