
Dengan pendalaman pembelajaran, pengetahuan kami sentiasa berkembang dan memperkaya. Adakah struktur pokok mengelirukan semua orang? Percayalah, selepas mempelajari gambar rajah, anda akan merasakan bahawa pokok binari adalah sangat mudah. Malah, pokok yang kita bicarakan ini juga merupakan bentuk graf yang istimewa.
Adakah anda masih ingat gambar pokok yang kita lihat dalam artikel pertama tentang pembelajaran tentang pokok?
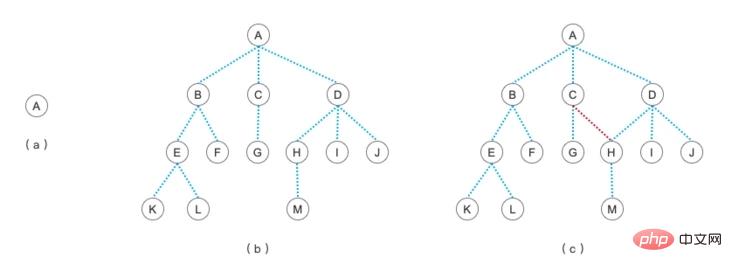
Masa tu kita kata gambar c tu bukan pokok, tapi gambar. kenapa? Daripada definisi pokok, kita dapat melihat bahawa pokok hanya boleh mempunyai satu nod akar, tidak boleh ada hubungan antara tahap, dan ia boleh mempunyai berbilang nod anak. Graf tidak perlu mengikut peraturan ini Ciri-ciri graf ialah nod boleh disambungkan antara satu sama lain. Sebagai contoh, gambar di bawah adalah semua gambar.
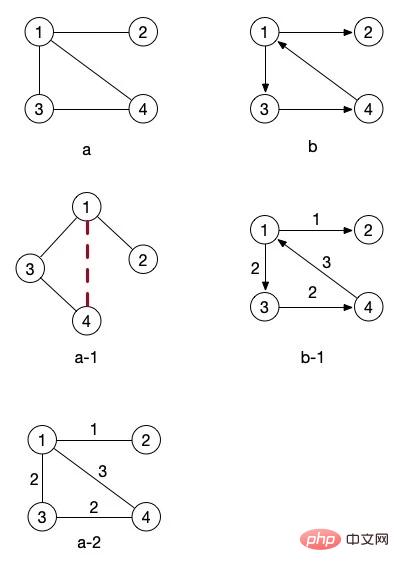
Dalam gambar yang dilukis di atas, gambar b mempunyai anak panah, manakala garis penghubung dalam gambar a tidak mempunyai arah yang jelas seperti ini graf terarah. Graf tanpa anak panah, iaitu graf tanpa arah, dipanggil graf tidak berarah.
Mula-mula kita alihkan perhatian kita kepada Rajah a-1 Sebenarnya, ia hanya berputar Rajah a. Bolehkah semua orang melihatnya? Jika anda mengabaikan sambungan antara nod 4 dan 1, maka ia adalah pokok. Adakah ia konsisten dengan konsep Rajah c dalam rajah pokok kami di atas?
Takrifan rasmi graf yang lebih formal ialah:
Graf G terdiri daripada dua set V dan E, dilambangkan sebagai G=(V, E), dengan V ialah bucu Tiada terhingga set kosong E ialah set terhingga bucu dalam V, dan bucu ini dipanggil tepi sama rata.
Dalam graf terarah, segmen garisan yang menghubungkan dua titik dari nod permulaan ke nod penunjuk boleh direkodkan sebagai
Adakah anda rasa lebih jelas apabila anda melihat gambar di atas, tetapi anda keliru apabila melihat definisi ini? Jika anda seorang pelajar yang perlu mengambil ujian, anda masih perlu menghafal definisi seperti ini. Jika anda hanya ingin fokus pada pembelajaran, aplikasi atau pemahaman seperti saya, tidak perlu menghafalnya secara hafalan. V ialah nod, dan E ialah hubungan antara nod ini Hubungan antara dua bucu, iaitu, segmen garisan yang menghubungkan nod pada graf ialah tepi.
OK, sekarang setelah ketiga-tiga konsep paling asas ini difahami, mari teruskan mempelajari istilah lain yang berkaitan dengan gambar!
Pertama sekali, kami menggunakan n untuk mewakili bilangan bucu dalam graf dan e untuk mewakili bilangan tepi Ingat kedua-dua kod ini.
(1) Subgraf: Katakan terdapat dua graf G=(V, E) dan G'=(V', E') jika V' terkandung dalam V dan E' dimasukkan dalam E, maka G' dipanggil subgraf G
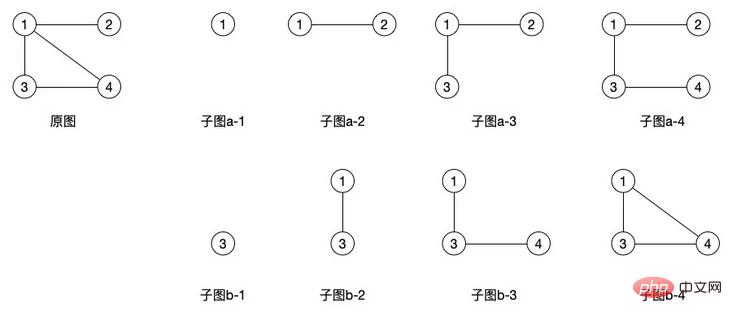
Subgraf di sebelah kanan dalam rajah di atas ialah semua subgraf asal imej , dapat dilihat bahawa subgraf boleh menjana banyak bentuk, dan graf terarah mempunyai konsep yang sama Namun, berbanding graf tidak terarah, graf terarah boleh menghasilkan lebih sedikit subgraf kerana tepinya berarah .
(2) Graf lengkap tidak berarah dan graf lengkap terarah: Untuk graf tidak berarah, jika ia mempunyai n(n-1)/2 tepi, ia ialah graf lengkap tidak berarah. Untuk graf terarah, jika ia mempunyai n(n-1) anak yatim, ia dipanggil graf lengkap terarah. (Rujuk pokok binari yang lengkap)
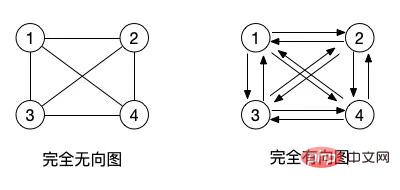
Malah, konsep graf lengkap ialah semua nod bersebelahan dalam graf mempunyai tepi yang boleh menghubungkan mereka bersama-sama.
Untuk graf terarah, walaupun tepi adalah arah, sudah tentu kita juga boleh menentukan arah ke belakang, seperti dan Kita perlu melukis dua anak panah dalam arah yang bertentangan untuk menunjukkan bahawa ia boleh pergi dari 1 ke 2 atau dari 2 ke 1. Dalam graf tidak terarah, satu tepi digunakan untuk menggantikan konsep kedua-dua tepi ini. Tepi tanpa arah anak panah adalah dua arah.
(3) Graf jarang dan graf tumpat: Graf dengan sedikit tepi atau anak yatim (seperti e
(4) Berat dan Bersih: Dalam aplikasi praktikal, setiap tepi atau tepi boleh ditandakan dengan nilai yang mempunyai beberapa makna, sama seperti jarak pada peta dipanggil pemberat. Gambar dengan kuasa boleh dipanggil rangkaian
Nombor pada sisi Rajah a-2 dan Rajah b-1 dalam gambar atas mewakili pemberat. Dua gambar ini boleh dipanggil gambar rangkaian. Kita akan mempelajari konsep pemberat kemudian apabila kita bercakap tentang algoritma yang berkaitan Daripada kedua-dua gambar ini, kita sebenarnya dapat melihat dengan jelas bahawa jika kita ingin pergi dari nod 1 ke nod 4, kita tidak pergi terus ke sebelah ini, tetapi lebih pantas untuk mengambil laluan
(5) Titik bersebelahan: Dua nod dengan tepi ialah titik bersebelahan
(6) Darjah, dalam darjah dan luar darjah : Darjah bucu v merujuk kepada bilangan tepi yang dikaitkan dengan v. Untuk graf terarah, anak panah yang menunjuk ke nod lain ialah darjah keluar, dan anak panah yang menunjuk ke arah dirinya sendiri ialah dalam darjah
Mari kita teruskan melihat Rajah b. Nod 1 mempunyai dua darjah keluar dan satu darjah. Ini nampaknya tidak memerlukan banyak penjelasan.
(7) Laluan dan panjang laluan: Semua bucu yang melalui satu bucu ke bucu lain ialah laluan. Jika ia adalah graf terarah, maka laluannya adalah dalam arah anak panah. Panjang laluan ialah bilangan tepi atau anak yatim yang melalui laluan
(8) Gelung atau gelung: Laluan yang bucu pertama dan bucu terakhirnya adalah sama dipanggil gelung atau gelung
(9) Ketersambungan, graf bersambung dan komponen bersambung: Jika terdapat laluan antara dua nod, ia dikatakan bersambung. Jika semua nod dalam keseluruhan graf boleh disambungkan antara satu sama lain, maka graf tersebut ialah graf bersambung. Komponen bersambung ialah subgraf bersambung maksimum dalam graf tidak berarah.
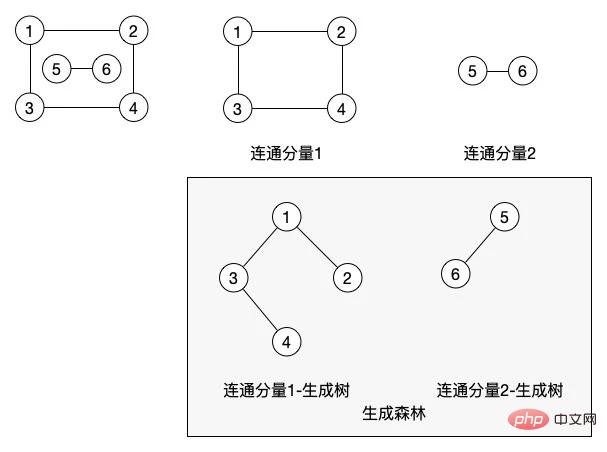
Termasuk tiga konsep berikut turut diberikan dalam gambar ini. Dalam graf tidak berarah, komponen bersambung adalah sama dengan subgraf bersambung maksimum Dalam graf ini, kita mempunyai dua komponen bersambung.
(10) Subgraf bersambung maksimum: Bilangan maksimum nod yang boleh terkandung dalam subgraf bersambung Jika satu lagi nod ditambah, subgraf itu tidak akan menjadi graf bersambung
(11) Pokok yang merangkumi: subgraph yang minimum, yang mengandungi semua simpul dalam graf, tetapi hanya tepi N-1 yang cukup untuk membentuk pokok. graf bersambung
sebenarnya adalah laluan yang menghubungkan semua nod dalam graf. Dalam graf komponen bersambung, kami menjana dua pokok rentang minimum berdasarkan dua komponen yang disambungkan. Nod pokok rentang komponen 1 yang disambungkan tidak semestinya perlu berada dalam struktur ini Kita boleh meletakkan nod 4 di bawah nod 2, bergantung pada cara kita melintasi untuk menjana pokok rentang minimum ini.
Pokok rentang minimum angka atas a kami sebenarnya boleh menjadi Rajah a-1 tanpa garis putus-putus merah. Sudah tentu, nod 4 juga boleh diletakkan di bawah nod 1. Ia juga bergantung pada cara program kami merentasi graf untuk menjana jenis pokok.
Adakah anda pening selepas membaca ini? Tidak mengapa, kami akan menggunakan istilah ini dengan kerap dalam kajian seterusnya, dan ini bukanlah yang paling komprehensif. Anda boleh merujuk kepada bibliografi dan bahan pembelajaran lain untuk kajian dan pemahaman yang lebih mendalam tentang istilah berkaitan graf.
Konsep graf telah hampir diperkenalkan Anda boleh menghadamnya sebelum meneruskan kajian kandungan berikut. Ini baru permulaan ramai pelajar akan merasakan perkara ini telah bertambah baik berbanding struktur pokok. Jangan takut, selepas mempelajari ilmu berikut, walaupun anda masih belum mengetahui kandungan berkaitan graf, anda pasti akan mempunyai pemahaman yang lebih mendalam tentang struktur pokok. kenapa? Pokok sebenarnya adalah graf tanpa gelung. Laluan mereka dicapai melalui kedalaman atau keluasan, tetapi grafnya lebih rumit. Sekarang, adakah anda merasakan bahawa masih ada harapan untuk masa depan? Pembelajaran selalunya merupakan proses yang beransur-ansur akan sentiasa ada kaitan antara pengetahuan semasa dan pengetahuan masa lalu.
Disyorkan: "Ringkasan soalan temuduga PHP 2021 (koleksi)" "tutorial video php"
Atas ialah kandungan terperinci Apakah gambar dalam php? Bagaimana ia boleh disimpan?. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
 Bagaimana untuk membuka fail php
Bagaimana untuk membuka fail php
 Bagaimana untuk mengalih keluar beberapa elemen pertama tatasusunan dalam php
Bagaimana untuk mengalih keluar beberapa elemen pertama tatasusunan dalam php
 Apa yang perlu dilakukan jika penyahserialisasian php gagal
Apa yang perlu dilakukan jika penyahserialisasian php gagal
 Bagaimana untuk menyambungkan php ke pangkalan data mssql
Bagaimana untuk menyambungkan php ke pangkalan data mssql
 Bagaimana untuk menyambung php ke pangkalan data mssql
Bagaimana untuk menyambung php ke pangkalan data mssql
 Bagaimana untuk memuat naik html
Bagaimana untuk memuat naik html
 Bagaimana untuk menyelesaikan aksara bercelaru dalam PHP
Bagaimana untuk menyelesaikan aksara bercelaru dalam PHP
 Bagaimana untuk membuka fail php pada telefon bimbit
Bagaimana untuk membuka fail php pada telefon bimbit