Pengesanan dan pemprosesan outlier data Python (contoh terperinci)

Artikel ini membawakan anda pengetahuan yang berkaitan tentang python terutamanya isu yang berkaitan dengan outlier dalam analisis data Secara amnya, kaedah pengesanan outlier termasuk kaedah statistik dan kaedah Kelas serta beberapa kaedah yang pakar dalam mengesan outlier, dsb. Kaedah ini diperkenalkan di bawah. Saya harap ia akan membantu semua orang.

Pembelajaran yang disyorkan: tutorial pembelajaran python

1 Apakah itu outlier?

Dalam pembelajaran mesin, pengesanan dan pemprosesan anomali ialah cabang yang agak kecil, atau dengan kata lain, hasil sampingan pembelajaran mesin, kerana secara umum masalah ramalan, Model biasanya merupakan ungkapan struktur data sampel keseluruhan Ungkapan ini biasanya menangkap sifat umum sampel keseluruhan, dan titik yang tidak konsisten sepenuhnya dengan sampel keseluruhan dari segi sifat ini dipanggil Titik tidak normal , biasanya. titik abnormal tidak dialu-alukan oleh pembangun dalam masalah ramalan, kerana masalah ramalan biasanya memfokuskan pada sifat sampel keseluruhan, dan mekanisme penjanaan titik abnormal adalah tidak konsisten sepenuhnya dengan sampel keseluruhan Jika model sensitif titik, model yang dihasilkan tidak boleh menyatakan sampel keseluruhan dengan baik, dan ramalannya akan menjadi tidak tepat. Sebaliknya, titik abnormal sangat menarik minat penganalisis dalam senario tertentu, seperti ramalan penyakit Biasanya penunjuk fizikal orang yang sihat adalah serupa dalam beberapa dimensi Jika seseorang itu ada kelainan pada dirinya penunjuk fizikal, maka keadaan fizikalnya mesti berubah dalam beberapa aspek Sudah tentu, perubahan ini tidak semestinya disebabkan oleh penyakit (sering dipanggil titik bunyi), tetapi kejadian dan pengesanan keabnormalan adalah titik permulaan yang penting. Senario serupa juga boleh digunakan untuk penipuan kredit, serangan siber, dsb.

2 Kaedah pengesanan untuk outlier

Kaedah pengesanan outlier am termasuk kaedah statistik, kaedah berasaskan kluster dan beberapa kaedah yang pakar dalam mengesan outlier Kaedah ini dibincangkan dengan sewajarnya.

1. Statistik mudah

Jika anda menggunakan pandas, kami boleh terus menggunakan describe() untuk memerhati huraian statistik data (hanya perhatikan secara kasar beberapa statistik), tetapi data statistik adalah jenis Berterusan, seperti berikut:

df.describe()

Atau hanya gunakan plot serakan untuk memerhati dengan jelas kewujudan outlier. Seperti yang ditunjukkan di bawah:

2. Prinsip 3∂

Prinsip ini mempunyai syarat: Data perlu mematuhi taburan normal . Di bawah prinsip 3∂, jika outlier melebihi 3 kali sisihan piawai, ia boleh dianggap sebagai outlier. Kebarangkalian positif atau negatif 3∂ ialah 99.7%, jadi kebarangkalian nilai selain daripada 3∂ daripada nilai purata yang muncul ialah P(|x-u| > 3∂) <= 0.003, yang sangat jarang dan kecil peristiwa kebarangkalian. Jika data tidak mengikut taburan normal, ia juga boleh diterangkan dengan berapa kali sisihan piawai berada jauh dari min.

Anak panah merah menghala ke luar.

3. Plot kotak

Kaedah ini menggunakan julat antara kuartil (IQR) plot kotak untuk mengesan outlier, juga dipanggil Ujian Tukey. Takrif plot kotak adalah seperti berikut:

Julat antara kuartil (IQR) ialah perbezaan antara kuartil atas dan kuartil bawah. Kami menggunakan 1.5 kali IQR sebagai standard dan menetapkan bahawa titik yang melebihi kuartil atas 1.5 kali jarak IQR, atau kuartil bawah -1.5 kali jarak IQR adalah outlier. Berikut ialah pelaksanaan kod dalam Python, terutamanya menggunakan kaedah numpy percentile.

Percentile = np.percentile(df['length'],[0,25,50,75,100])
IQR = Percentile[3] - Percentile[1]
UpLimit = Percentile[3]+ageIQR*1.5
DownLimit = Percentile[1]-ageIQR*1.5

Anda juga boleh menggunakan seaborn kaedah visualisasi boxplot untuk mencapai ini:

f,ax=plt.subplots(figsize=(10,8))
sns.boxplot(y='length',data=df,ax=ax)
plt.show()

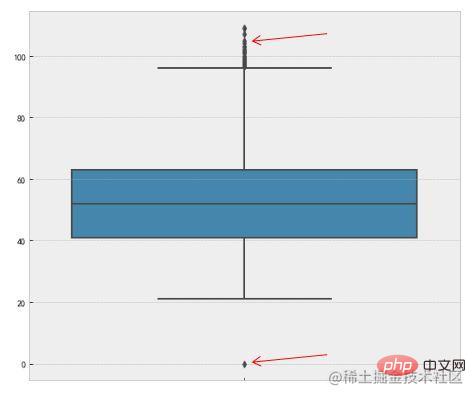
Anak panah merah menunjuk ke yang terpencil.

Di atas ialah kaedah mudah yang biasa digunakan untuk menentukan outlier. Mari perkenalkan beberapa algoritma pengesanan luar yang lebih kompleks Memandangkan ia melibatkan banyak kandungan, hanya rakan-rakan yang berminat boleh belajar secara mendalam.

4. Berdasarkan pengesanan model

Kaedah ini secara amnya membina model taburan kebarangkalian dan mengira kebarangkalian objek itu mematuhi model dan merawat objek dengan rendah kebarangkalian sebagai outlier. Jika model ialah himpunan kluster, anomali ialah objek yang tidak tergolong dalam mana-mana kluster jika model adalah regresi, anomali ialah objek yang agak jauh daripada nilai yang diramalkan.

Takrif kebarangkalian bagi outlier: Outlier ialah objek yang mempunyai kebarangkalian rendah berkenaan dengan model taburan kebarangkalian data. Prasyarat untuk situasi ini adalah untuk mengetahui pengedaran yang dipatuhi oleh set data Jika anggaran salah, ia akan menyebabkan pengedaran berat.

Sebagai contoh, kaedah RobustScaler dalam kejuruteraan ciri, apabila menskalakan nilai ciri data, akan menggunakan pengedaran kuantil ciri data untuk membahagikan data kepada berbilang segmen berdasarkan kuantil dan hanya menggunakan segmen tengah untuk penskalaan. , sebagai contoh, hanya ambil data daripada kuantil 25% kepada kuantil 75% untuk penskalaan. Ini mengurangkan kesan data yang tidak normal.

Kelebihan dan Kekurangan: (1) Terdapat asas teori yang kukuh dalam statistik, dan ujian ini boleh menjadi sangat berkesan apabila terdapat data dan pengetahuan yang mencukupi tentang jenis ujian yang digunakan; 2) Untuk Untuk data multivariate, lebih sedikit pilihan tersedia dan untuk data dimensi tinggi, kemungkinan pengesanan ini adalah lemah.

5. Pengesanan outlier berdasarkan kedekatan

Kaedah statistik menggunakan pengedaran data untuk memerhatikan outlier Sesetengah kaedah memerlukan beberapa syarat pengedaran, tetapi dalam amalan pengedaran data adalah sangat Ia adalah sukar untuk memenuhi beberapa andaian dan mempunyai had tertentu dalam penggunaan.

Lebih mudah untuk menentukan ukuran kedekatan yang bermakna bagi set data daripada menentukan taburan statistiknya. Kaedah ini lebih umum dan lebih mudah untuk digunakan berbanding kaedah statistik kerana skor outlier objek diberikan oleh jarak ke jiran k-terdekatnya (KNN).

Perlu diambil perhatian bahawa skor outlier sangat sensitif terhadap nilai k. Jika k terlalu kecil, sebilangan kecil outlier berdekatan mungkin menghasilkan skor outlier yang rendah jika K terlalu besar, semua objek dalam kelompok dengan mata kurang daripada k boleh menjadi outlier. Untuk menjadikan skema ini lebih mantap kepada pemilihan k, jarak purata k jiran terdekat boleh digunakan.

Kebaikan dan keburukan: (1) Mudah; (2) Kelemahan: Kaedah berasaskan kedekatan memerlukan masa O(m2) dan tidak sesuai untuk set data yang besar; ) Kaedah ini juga sensitif kepada pilihan parameter; (4) ia tidak boleh mengendalikan set data dengan kawasan ketumpatan yang berbeza, kerana ia menggunakan ambang global dan tidak boleh mengambil kira perubahan ketumpatan tersebut.

5. Pengesanan outlier berasaskan kepadatan

Dari perspektif berasaskan kepadatan, outlier ialah objek dalam kawasan berketumpatan rendah. Pengesanan outlier berasaskan ketumpatan berkait rapat dengan pengesanan outlier berasaskan kedekatan, kerana ketumpatan sering ditakrifkan dari segi kedekatan. Cara biasa untuk mentakrifkan ketumpatan adalah dengan mentakrifkan ketumpatan sebagai salingan jarak purata ke k jiran terdekat. Jika jarak ini kecil, ketumpatannya tinggi dan begitu juga sebaliknya. Satu lagi definisi ketumpatan ialah Takrifan ketumpatan yang digunakan oleh algoritma pengelompokan DBSCAN, iaitu, ketumpatan di sekeliling objek adalah sama dengan bilangan objek dalam jarak d tertentu dari objek.

Kebaikan dan Kelemahan: (1) Memberi ukuran kuantitatif bahawa objek adalah outlier, dan boleh mengendalikannya dengan baik walaupun data mempunyai kawasan yang berbeza; kaedah berasaskan jarak, kaedah ini semestinya mempunyai kerumitan masa O(m2). Untuk data berdimensi rendah, menggunakan struktur data tertentu boleh mencapai O(mlogm); (3) Pemilihan parameter adalah sukar. Walaupun algoritma LOF mengendalikan masalah ini dengan memerhatikan nilai k yang berbeza dan kemudian mendapatkan skor outlier maksimum, masih perlu memilih sempadan atas dan bawah untuk nilai ini.

6. Kaedah berasaskan pengelompokan untuk pengesanan terpencil

Pencilan berasaskan pengelompokan: Objek ialah pencilan berdasarkan pengelompokan Jika objek itu tidak tergolong dalam mana-mana kelompok, maka objek kepunyaan outlier.

Pengaruh outlier pada pengelompokan awal: Jika outlier dikesan melalui pengelompokan, terdapat persoalan kerana outlier mempengaruhi pengelompokan: sama ada struktur itu sah. Ini juga merupakan kelemahan algoritma k-means, yang sensitif kepada outlier. Untuk menangani masalah ini, anda boleh menggunakan kaedah berikut: objek kluster, padam outlier dan objek kluster sekali lagi (ini tidak menjamin hasil yang optimum).

Kebaikan dan Kelemahan: (1) Teknik pengelompokan berdasarkan kerumitan linear dan hampir-linear (k-means) mungkin sangat berkesan dalam menemui outlier; (2) Definisi kelompok Ia adalah biasanya pelengkap outlier, jadi adalah mungkin untuk mencari cluster dan outlier pada masa yang sama; (3) set outlier yang terhasil dan skor mereka mungkin sangat bergantung pada bilangan cluster yang digunakan dan kewujudan outlier dalam data; 4) Kualiti kluster yang dihasilkan oleh algoritma kluster mempunyai kesan yang besar terhadap kualiti kluster yang dihasilkan oleh algoritma.

7. Pengesanan outlier khusus

Malah, niat asal kaedah pengelompokan yang dinyatakan di atas adalah pengelasan tanpa pengawasan, bukan untuk mencari outlier, tetapi kebetulan fungsinya dapat Pengesanan outlier ialah fungsi terbitan.

Selain kaedah yang dinyatakan di atas, terdapat dua kaedah yang lebih biasa digunakan khusus untuk mengesan titik abnormal: One Class SVM dan Isolation Forest Butirannya tidak akan dikaji secara mendalam.

3 Cara menangani outlier

Outlier telah dikesan dan kita perlu mengendalikannya pada tahap tertentu. Kaedah umum pengendalian outlier boleh dibahagikan secara kasar kepada kategori berikut:

• Padamkan rekod yang mengandungi outlier: Padamkan rekod yang mengandungi outlier secara langsung
• Anggap sebagai nilai yang tiada: Anggap outlier sebagai Nilai yang tiada diproses menggunakan kaedah pemprosesan nilai yang hilang;
• Pembetulan nilai min: Outlier boleh dibetulkan dengan purata dua nilai yang diperhatikan sebelum dan selepas; Tiada pemprosesan
: Menjalankan perlombongan data secara langsung pada set data dengan outlier;
• Sama ada outlier perlu dipadamkan boleh dipertimbangkan berdasarkan situasi sebenar. Oleh kerana sesetengah model tidak begitu sensitif kepada outlier, walaupun terdapat outlier, kesan model tidak akan terjejas Walau bagaimanapun, sesetengah model seperti LR regresi logistik sangat sensitif terhadap outlier Jika tidak diproses, kesan yang sangat buruk seperti overfitting mungkin berlaku.

4 Ringkasan outlier

Di atas ialah ringkasan kaedah pengesanan dan pemprosesan outlier.

Kita boleh mencari outlier melalui beberapa kaedah pengesanan, tetapi keputusan yang diperolehi tidak betul-betul betul Situasi khusus perlu dinilai berdasarkan pemahaman perniagaan. Begitu juga cara menangani outlier, sama ada ia perlu dipadam, diperbetulkan, atau tidak diproses, juga perlu dipertimbangkan berdasarkan situasi sebenar dan tidak diperbaiki.

Pembelajaran yang disyorkan:

tutorial python

Atas ialah kandungan terperinci Pengesanan dan pemprosesan outlier data Python (contoh terperinci). Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!