Penjelasan terperinci tentang pokok AVL struktur data Java
Artikel ini membawakan anda pengetahuan yang berkaitan tentang java, yang terutamanya memperkenalkan pengetahuan yang berkaitan tentang pokok binari seimbang (pokok AVL pada dasarnya adalah pokok binari dengan fungsi pengimbangan lihatlah, semoga bermanfaat untuk semua.

Pembelajaran yang disyorkan: "tutorial video java"
Pengenalan pokok AVL
Pencarian pokok binari mempunyai sangat tinggi Kecekapan carian adalah tinggi, tetapi situasi melampau berikut akan berlaku apabila mencari pepohon binari: 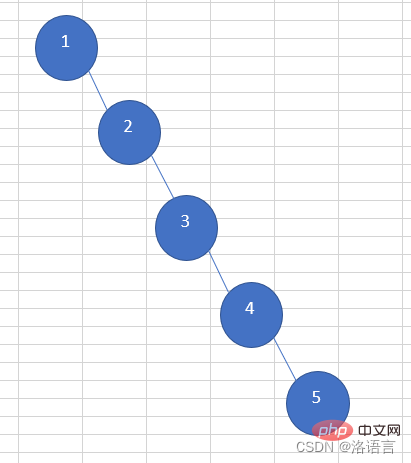
Kecekapan carian pepohon perduaan sedemikian adalah lebih rendah daripada senarai terpaut. Pokok binari seimbang (pokok AVL) yang muncul berdasarkan pokok binari carian menyelesaikan masalah ini. Apabila nilai mutlak perbezaan ketinggian antara subpokok kiri dan kanan nod dalam pokok binari seimbang (pokok AVL) lebih besar daripada 1, perbezaan ketinggian mereka akan dikurangkan melalui operasi putaran.
Konsep asas
Pokok AVL pada asasnya ialah pepohon carian binari ialah:
- itu sendiri adalah yang pertama
二叉搜索树. -
高度之差的绝对值(平衡因子)最多为1subpokok kiri dan kanan setiap nod. Dalam erti kata lain, pokok AVL pada dasarnya ialah pokok carian binari dengan平衡功能(pokok pengisihan binari, pokok carian binari). - Apabila nod dimasukkan atau dipadamkan, nilai mutlak perbezaan ketinggian antara subpokok kiri dan kanan nod adalah lebih besar daripada 1. Dalam kes ini, pokok binari perlu diseimbangkan semula melalui operasi daripada
左旋dan右旋negeri.
Faktor Baki (balanceFactor)
-
高度之差subpokok kiri dan subpokok kanan nod. - BF mana-mana nod dalam pepohon AVL hanya boleh
-1,0和1。
Reka bentuk asas
Berikut ialah kaedah dan atribut mudah yang diperlukan oleh AVL pokok:
public class AVLTree <e>>{
class Node{
E value;
Node left;
Node right;
int height;
public Node(){}
public Node(E value){
this.value = value;
height = 1;
left = null;
right = null;
}
public void display(){
System.out.print(this.value + " ");
}
}
Node root;
int size;
public int size(){
return size;
}
public int getHeight(Node node) {
if(node == null) return 0;
return node.height;
}
//获取平衡因子(左右子树的高度差,大小为1或者0是平衡的,大小大于1不平衡)
public int getBalanceFactor(){
return getBalanceFactor(root);
}
public int getBalanceFactor(Node node){
if(node == null) return 0;
return getHeight(node.left) - getHeight(node.right);
}
//判断一个树是否是一个平衡二叉树
public boolean isBalance(Node node){
if(node == null) return true;
int balanceFactor = Math.abs(getBalanceFactor(node.left) - getBalanceFactor(node.right));
if(balanceFactor > 1) return false;
return isBalance(node.left) && isBalance(node.right);
}
public boolean isBalance(){
return isBalance(root);
}
//中序遍历树
private void inPrevOrder(Node root){
if(root == null) return;
inPrevOrder(root.left);
root.display();
inPrevOrder(root.right);
}
public void inPrevOrder(){
System.out.print("中序遍历:");
inPrevOrder(root);
}}</e>RR (kidal)
Masukkan nod ke dalam subpokok kanan subpokok kanan pokok, menyebabkan pokok binari menjadi tidak seimbang seperti yang ditunjukkan dalam rajah di bawah, masukkan 5 ke dalam pokok binari seimbang Akibatnya, pokok menjadi tidak seimbang, dan operasi belok kiri diperlukan, seperti berikut: 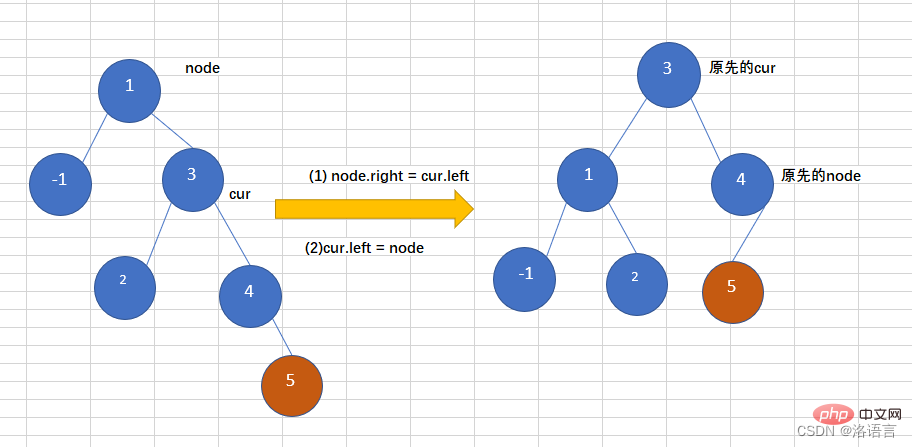
Kodnya adalah seperti berikut:
//左旋,并且返回新的根节点
public Node leftRotate(Node node){
System.out.println("leftRotate");
Node cur = node.right;
node.right = cur.left;
cur.left = node;
//跟新node和cur的高度
node.height = Math.max(getHeight(node.left),getHeight(node.right)) + 1;
cur.height = Math.max(getHeight(cur.left),getHeight(cur.right)) + 1;
return cur;
}LL (belok kanan)
Ke arah Memasukkan nod ke dalam subpokok kiri subpokok kiri pokok AVL menyebabkan pokok binari menjadi tidak seimbang, seperti yang ditunjukkan dalam rajah di bawah 2 ke dalam pokok binari seimbang menyebabkan pokok menjadi tidak seimbang Pada masa ini, operasi belok kiri diperlukan, seperti berikut: 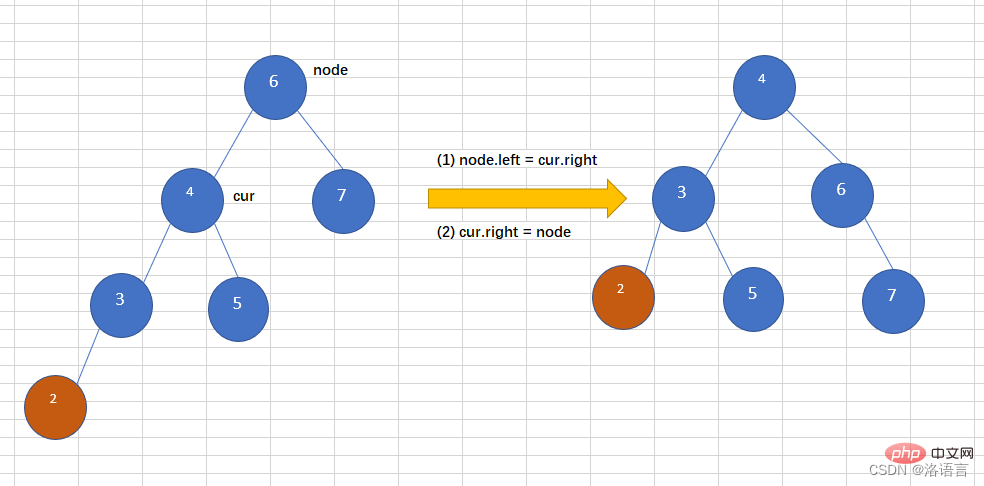
Kodnya adalah seperti berikut:
//右旋,并且返回新的根节点
public Node rightRotate(Node node){
System.out.println("rightRotate");
Node cur = node.left;
node.left = cur.right;
cur.right = node;
//跟新node和cur的高度
node.height = Math.max(getHeight(node.left),getHeight(node.right)) + 1;
cur.height = Math.max(getHeight(cur.left),getHeight(cur.right)) + 1;
return cur;
}, menyebabkan pokok menjadi tidak seimbang Anda perlu menjajarkan
dahulu, dan kemudian di bawah, nod yang dimasukkan ialah 2.左子树的右子树左子树进行左旋整棵树右旋
Tambah nod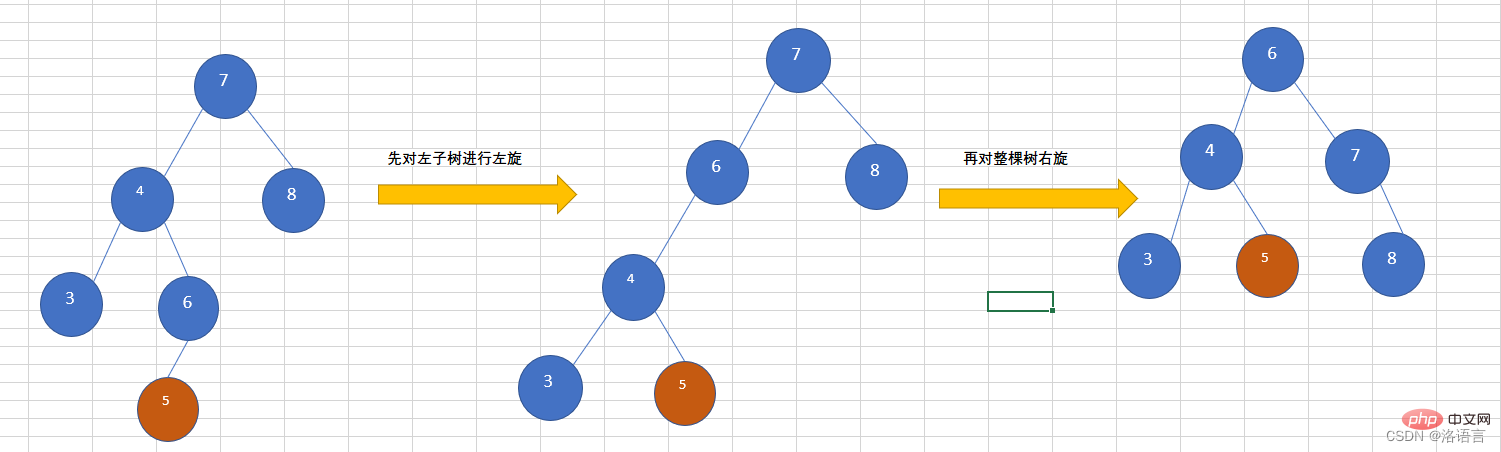
Padam nod
右子树的左子树Pembelajaran yang disyorkan: "右子树进行右旋java tutorial video整棵树左旋"
Atas ialah kandungan terperinci Penjelasan terperinci tentang pokok AVL struktur data Java. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

Video Face Swap
Tukar muka dalam mana-mana video dengan mudah menggunakan alat tukar muka AI percuma kami!

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1393
1393
 52
52
 1205
1205
 24
24
 Nombor Sempurna di Jawa
Aug 30, 2024 pm 04:28 PM
Nombor Sempurna di Jawa
Aug 30, 2024 pm 04:28 PM
Panduan Nombor Sempurna di Jawa. Di sini kita membincangkan Definisi, Bagaimana untuk menyemak nombor Perfect dalam Java?, contoh dengan pelaksanaan kod.
 Weka di Jawa
Aug 30, 2024 pm 04:28 PM
Weka di Jawa
Aug 30, 2024 pm 04:28 PM
Panduan untuk Weka di Jawa. Di sini kita membincangkan Pengenalan, cara menggunakan weka java, jenis platform, dan kelebihan dengan contoh.
 Nombor Smith di Jawa
Aug 30, 2024 pm 04:28 PM
Nombor Smith di Jawa
Aug 30, 2024 pm 04:28 PM
Panduan untuk Nombor Smith di Jawa. Di sini kita membincangkan Definisi, Bagaimana untuk menyemak nombor smith di Jawa? contoh dengan pelaksanaan kod.
 Soalan Temuduga Java Spring
Aug 30, 2024 pm 04:29 PM
Soalan Temuduga Java Spring
Aug 30, 2024 pm 04:29 PM
Dalam artikel ini, kami telah menyimpan Soalan Temuduga Spring Java yang paling banyak ditanya dengan jawapan terperinci mereka. Supaya anda boleh memecahkan temuduga.
 Cuti atau kembali dari Java 8 Stream Foreach?
Feb 07, 2025 pm 12:09 PM
Cuti atau kembali dari Java 8 Stream Foreach?
Feb 07, 2025 pm 12:09 PM
Java 8 memperkenalkan API Stream, menyediakan cara yang kuat dan ekspresif untuk memproses koleksi data. Walau bagaimanapun, soalan biasa apabila menggunakan aliran adalah: bagaimana untuk memecahkan atau kembali dari operasi foreach? Gelung tradisional membolehkan gangguan awal atau pulangan, tetapi kaedah Foreach Stream tidak menyokong secara langsung kaedah ini. Artikel ini akan menerangkan sebab -sebab dan meneroka kaedah alternatif untuk melaksanakan penamatan pramatang dalam sistem pemprosesan aliran. Bacaan Lanjut: Penambahbaikan API Java Stream Memahami aliran aliran Kaedah Foreach adalah operasi terminal yang melakukan satu operasi pada setiap elemen dalam aliran. Niat reka bentuknya adalah
 TimeStamp to Date in Java
Aug 30, 2024 pm 04:28 PM
TimeStamp to Date in Java
Aug 30, 2024 pm 04:28 PM
Panduan untuk TimeStamp to Date di Java. Di sini kita juga membincangkan pengenalan dan cara menukar cap waktu kepada tarikh dalam java bersama-sama dengan contoh.
 Program Java untuk mencari kelantangan kapsul
Feb 07, 2025 am 11:37 AM
Program Java untuk mencari kelantangan kapsul
Feb 07, 2025 am 11:37 AM
Kapsul adalah angka geometri tiga dimensi, terdiri daripada silinder dan hemisfera di kedua-dua hujungnya. Jumlah kapsul boleh dikira dengan menambahkan isipadu silinder dan jumlah hemisfera di kedua -dua hujungnya. Tutorial ini akan membincangkan cara mengira jumlah kapsul yang diberikan dalam Java menggunakan kaedah yang berbeza. Formula volum kapsul Formula untuk jumlah kapsul adalah seperti berikut: Kelantangan kapsul = isipadu isipadu silinder Dua jumlah hemisfera dalam, R: Radius hemisfera. H: Ketinggian silinder (tidak termasuk hemisfera). Contoh 1 masukkan Jejari = 5 unit Ketinggian = 10 unit Output Jilid = 1570.8 Unit padu menjelaskan Kirakan kelantangan menggunakan formula: Kelantangan = π × r2 × h (4
 Cipta Masa Depan: Pengaturcaraan Java untuk Pemula Mutlak
Oct 13, 2024 pm 01:32 PM
Cipta Masa Depan: Pengaturcaraan Java untuk Pemula Mutlak
Oct 13, 2024 pm 01:32 PM
Java ialah bahasa pengaturcaraan popular yang boleh dipelajari oleh pembangun pemula dan berpengalaman. Tutorial ini bermula dengan konsep asas dan diteruskan melalui topik lanjutan. Selepas memasang Kit Pembangunan Java, anda boleh berlatih pengaturcaraan dengan mencipta program "Hello, World!" Selepas anda memahami kod, gunakan gesaan arahan untuk menyusun dan menjalankan program, dan "Hello, World!" Pembelajaran Java memulakan perjalanan pengaturcaraan anda, dan apabila penguasaan anda semakin mendalam, anda boleh mencipta aplikasi yang lebih kompleks.




