Artikel ini membawakan anda pengetahuan yang berkaitan tentang python Ia terutamanya memperkenalkan isu berkaitan tentang pengisihan gelembung, termasuk penerangan algoritma, analisis, pelaksanaan kod, dsb. Berikut ialah Mari kita lihat, harap ia membantu semua orang. .
Pembelajaran yang disyorkan: tutorial video python
Isih Buih (Isih Buih) ialah algoritma pengisihan yang mudah. Ia berulang kali berulang melalui tatasusunan untuk diisih, membandingkan dua elemen pada satu masa dan menukarnya jika ia berada dalam susunan yang salah. Kerja melintasi tatasusunan diulang sehingga tiada lagi pertukaran diperlukan, yang bermaksud tatasusunan telah diisih. Nama algoritma ini berasal dari fakta bahawa elemen yang lebih kecil akan perlahan-lahan "terapung" ke bahagian atas tatasusunan melalui pertukaran.
1. Jika yang pertama lebih besar daripada yang kedua (dalam tertib menaik), tukar kedua-duanya.
2. Lakukan perkara yang sama untuk setiap pasangan elemen bersebelahan, daripada pasangan pertama di awal hingga pasangan terakhir di penghujung. Selepas langkah ini selesai, elemen terakhir akan menjadi nombor terbesar.
3. Ulang langkah di atas untuk semua elemen kecuali yang terakhir.
4 Teruskan mengulangi langkah di atas untuk semakin sedikit elemen setiap kali sehingga tiada pasangan nombor yang tinggal. Perlu membandingkan.
Kemudian kita perlu melakukan proses menggelegak n-1, dan bilangan perbandingan yang sepadan untuk setiap kali adalah seperti yang ditunjukkan di bawah:
Sekarang kita memahami proses berjalan, mari kita lihat pelaksanaan GIF:
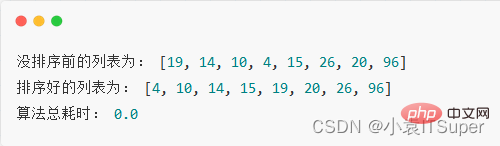
Kami mengisih senarai tidak tertib berikut
Pelaksanaan kod:
import timepop_list = [19, 14, 10, 4, 15, 26, 20, 96]print("没排序前的列表为：", pop_list)# 记录开始时间start = time.time()# 外层循环控制轮数for i in range(len(pop_list) - 1):
# 内层循环控制比较次数
for j in range(len(pop_list) - i - 1):
# 如果前一个数字比后一个数字大，就交换位置
if pop_list[j] > pop_list[j + 1]:
# python特有交换位置方式
pop_list[j], pop_list[j + 1] = pop_list[j + 1], pop_list[j]print("排序好的列表为：", pop_list)# 记录结束时间end = time.time()print("算法总耗时：", end - start)Hasil berjalan:
Bilangan pembolehubah ditakrifkan dalam gelung. , jika kiraan tidak berubah selepas gelung pertama, ini bermakna input adalah urutan tertib Pada masa ini, kami terus kembali untuk keluar dari gelung Kerumitan masa pada masa ini ialah
O(n)
Kod pelaksanaan:
import timedef bubble_sort(pop_list):
for j in range(len(pop_list) - 1, 0, -1):
count = 0
for i in range(0, j):
if pop_list[i] > pop_list[i + 1]:
pop_list[i], pop_list[i + 1] = pop_list[i + 1], pop_list[i]
count += 1
if count == 0:
returnpop_list = [19, 14, 10, 4, 15, 26, 20, 96]print("没排序前的列表为：", pop_list)# 记录开始时间start = time.time()bubble_sort(pop_list)print("排序好的列表为：", pop_list)# 记录结束时间end = time.time()print("算法总耗时：", end - start)Hasil jalankan: 
tutorial video python
- Kerumitan masa optimum:
O(n)(Menunjukkan bahawa selepas merentasi, didapati tiada unsur yang boleh ditukar, dan pengisihan tamat.)- Kerumitan masa paling teruk:
O(n^2)- Kestabilan: Stabil
Apabila jumlah bilangan elemen tatasusunan ialah N, jumlah bilangan perbandingan yang diperlukan ialah:- perbandingan. Oleh kerana data ditukar hanya apabila elemen sebelumnya lebih besar daripada elemen berikut, bilangan swap adalah kurang daripada bilangan perbandingan. Jika data adalah rawak dan kira-kira separuh daripada data perlu ditukar, bilangan pertukaran ialah
(N-1) (N-2) (N-3) ...1=N*(N-1)/2
Algoritma membuat kira-kira- (tetapi dalam kes yang paling teruk, apabila data awal dalam susunan terbalik, setiap perbandingan memerlukan pertukaran).
.N^2/2N^2/4
Bilangan pertukaran dan operasi perbandingan adalah berkadar dengan N^2 Memandangkan dalam tatatanda O besar, pemalar diabaikan, pengisihan gelembung adalah kompleks masa ijazah ialah- Pembelajaran yang disyorkan:
O(N^2)
Atas ialah kandungan terperinci Penjelasan grafik terperinci algoritma jenis gelembung Python. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
![[Web front-end] Permulaan pantas Node.js](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
