
Artikel ini membawakan anda pengetahuan yang berkaitan tentang Python Ia terutamanya menganjurkan isu yang berkaitan dengan model hutan rawak, termasuk pengenalan kepada model ensemble, prinsip asas model hutan rawak dan penggunaan. sklearn untuk melaksanakan rawak Mari kita lihat model hutan dan kandungan lain saya harap ia akan membantu semua orang.

[Cadangan berkaitan: Tutorial video Python3 ]
Menggunakan pembelajaran ensemble model Satu siri pelajar lemah (juga dipanggil model asas atau model asas) mempelajari dan menyepadukan keputusan setiap pelajar lemah untuk memperoleh hasil pembelajaran yang lebih baik daripada pelajar tunggal.
Terdapat dua algoritma biasa untuk model pembelajaran bersepadu: Algoritma Bagging dan Algoritma Boosting.
Model pembelajaran mesin biasa bagi algoritma Bagging ialah model hutan rawak, manakala model pembelajaran mesin biasa bagi algoritma Boosting ialah model AdaBoost, GBDT, XGBoost dan LightGBM.
Prinsip algoritma Bagging adalah serupa dengan undian Setiap pelajar lemah mempunyai satu undian Akhirnya, berdasarkan undian semua pelajar lemah, ia dijana mengikut prinsip "minoriti patuh majoriti" Keputusan ramalan akhir ditunjukkan dalam rajah di bawah.
Andaikan terdapat 10,000 keping data asal, dan 10,000 data diekstrak secara rawak dengan penggantian untuk membentuk set latihan baharu (kerana ia rawak dengan penggantian) Pensampelan belakang, jadi sekeping data tertentu boleh dijadikan sampel beberapa kali, atau sekeping data tertentu tidak boleh dijadikan sampel sekali), setiap kali set latihan digunakan untuk melatih pelajar yang lemah. Dengan cara ini, selepas pensampelan secara rawak n kali dengan penggantian, pada akhir latihan, n pelajar lemah yang dilatih oleh set latihan yang berbeza boleh diperolehi Mengikut keputusan ramalan pelajar lemah ini, mengikut prinsip "the minoriti mematuhi majoriti" , untuk mendapatkan keputusan ramalan akhir yang lebih tepat dan munasabah.
Khususnya, dalam masalah klasifikasi, n pelajar lemah digunakan untuk mengundi untuk mendapatkan keputusan akhir, dan dalam masalah regresi, n pelajar lemah digunakan untuk memperoleh keputusan akhir Nilai purata pelajar digunakan sebagai hasil akhir.
Intipati algoritma Boosting adalah untuk menggalakkan pelajar yang lemah menjadi pelajar yang kuat Perbezaan antara algoritma Bagging ialah algoritma Bagging memperlakukan semua pelajar yang lemah secara sama rata algoritma akan "melayan" pelajar lemah secara berbeza Dalam istilah orang awam, ia memberi tumpuan kepada "memupuk golongan elit" dan "memperhatikan kesilapan."
"Memupuk golongan elit" bermaksud memberi berat yang lebih besar kepada pelajar lemah dengan keputusan ramalan yang lebih tepat selepas setiap pusingan latihan, dan mengurangkan berat pelajar lemah yang berprestasi rendah . Dengan cara ini, dalam ramalan akhir, "model yang sangat baik" mempunyai berat yang besar, yang bersamaan dengan ia boleh membuang berbilang undi, manakala "model umum" hanya boleh membuang satu undi atau tidak boleh mengundi.
"Beri perhatian kepada kesilapan" bermaksud menukar berat atau taburan kebarangkalian set latihan selepas setiap pusingan latihan, dengan meningkatkan berat contoh yang telah diramalkan secara salah oleh pelajar lemah dalam pusingan sebelumnya, mengurangkan Berat sampel yang diramalkan dengan betul oleh pelajar lemah dalam pusingan sebelumnya adalah untuk meningkatkan penekanan pelajar lemah pada data yang telah diramalkan secara salah, sekali gus meningkatkan kesan ramalan keseluruhan model.
Hutan Rawak (Hutan Rawak) ialah model bagging klasik, dan pelajar lemahnya ialah model pokok keputusan. Seperti yang ditunjukkan dalam rajah di bawah, model hutan rawak akan mengambil sampel secara rawak daripada set data asal untuk membentuk n set data sampel yang berbeza, dan kemudian membina n model pepohon keputusan yang berbeza berdasarkan set data ini Akhirnya, berdasarkan purata daripada nilai model pokok keputusan ini (untuk model regresi) atau undian (untuk model klasifikasi) untuk mendapatkan keputusan akhir.
Untuk memastikan kebolehan generalisasi (atau keupayaan umum) model, model hutan rawak sering mengikuti "data" semasa membina setiap pokok. Dua prinsip asas ialah "rawak" dan "rawak ciri".
Data rawak: Ekstrak data secara rawak daripada semua data dengan penggantian sebagai data latihan untuk salah satu model pepohon keputusan. Sebagai contoh, terdapat 1,000 data asal, diekstrak 1,000 kali dengan penggantian, untuk membentuk set data baharu untuk melatih model pokok keputusan tertentu.
Ciri rawak: Jika dimensi ciri setiap sampel ialah M, nyatakan k
Berbanding dengan model pepohon keputusan tunggal, model hutan rawak menyepadukan berbilang pepohon keputusan, jadi keputusan ramalannya akan lebih tepat, ia tidak akan mudah menyebabkan pemadanan yang berlebihan, dan ia akan mempunyai generalisasi yang lebih kukuh kebolehan.
Model hutan rawak boleh melakukan kedua-dua analisis pengelasan dan analisis regresi Model yang sepadan ialah:
· Model Pengelasan hutan rawak. (RandomForestClassifier)
·Model Regresi Hutan Rawak (RandomForestRegressor)
Pelajar lemah model pengelasan hutan rawak ialah model pokok keputusan pengelasan, hutan rawak regresi Pelajar model yang lemah ialah model pepohon keputusan regresi.
Kodnya adalah seperti berikut.
from sklearn.ensemble import RandomForestClassifier X = [[1,2],[3,4],[5,6],[7,8],[9,10]] y = [0,0,0,1,1] # 设置弱学习器数量为10 model = RandomForestClassifier(n_estimators=10,random_state=123) model.fit(X,y) model.predict([[5,5]]) # 输出为:array([0])
Bahagian ini menerangkan cara menggunakan data asas saham untuk mendapatkan beberapa derivatif data berubah-ubah, seperti Penunjuk purata bergerak yang biasa digunakan dalam analisis teknikal saham termasuk harga purata bergerak 5 hari MA5 dan harga purata bergerak 10 hari MA10, penunjuk kekuatan relatif RSI, penunjuk momentum MOM, purata bergerak eksponen EMA, persamaan dan perbezaan purata bergerak MACD, dsb.
Mula-mula gunakan fungsi get_k_data() untuk mendapatkan data stok asas dari 2015-01-01 hingga 2019-12-31 Kodnya adalah seperti berikut .
5 baris pertama data ditunjukkan dalam rajah di bawah. Data yang hilang ialah data hari cuti (bukan hari dagangan).
Gunakan fungsi set_index() untuk menetapkan lajur tarikh kepada indeks baris , kodnya adalah seperti berikut.
Sesetengah data pembolehubah terbitan ringkas boleh dijana melalui kod berikut.
maksud tutup-buka (harga tutup - harga pembukaan)/harga pembukaan
bermaksud tinggi-rendah (harga tertinggi - Harga terendah)/harga terendah;
pre_close mewakili harga penutupan semalam Gunakan shift(1) untuk mengalihkan semua data dalam lajur tutup ke bawah 1 baris dan membentuk lajur baharu. - 1) bermaksud naik 1 baris;
harga_perubahan mewakili harga tutup hari ini - harga penutup semalam, iaitu perubahan harga saham pada hari tersebut; perubahan harga saham pada hari tersebut, juga dikenali sebagai Ia adalah kenaikan atau penurunan harga saham pada hari tersebut.
4.1.3 Jana nilai MA penunjuk purata bergerak
Contohnya: Pengiraan MA5Antaranya, MA bermaksud purata bergerak, " "Purata " merujuk kepada min aritmetik bagi harga penutupan n hari terakhir, dan "bergerak" bermakna data harga bagi n hari terakhir sentiasa digunakan dalam pengiraan.
Apabila mengira data seperti MA5, kerana jumlah data dalam 4 hari pertama tidak mencukupi, purata bergerak sepadan dengan 4 hari ini tidak boleh dikira, jadi nilai nol NaN akan dijana. Biasanya, fungsi dropna() digunakan untuk memadam nilai nol untuk mengelakkan masalah yang disebabkan oleh nilai nol dalam pengiraan berikutnya.
Mengikut data di atas, nilai MA5 No. 5 ialah (1.2+1.4+1. 6+1.8+2.0 )/5=1.6, dan nilai MA5 No. 6 ialah (1.4+1.6+1.8+2.0+2.2)/5=1.8 dan seterusnya. Purata pergerakan harga saham dalam satu tempoh masa disambungkan ke dalam lengkung, iaitu purata bergerak. Begitu juga, MA10 ialah harga saham purata 10 hari sebelumnya dari hari pengiraan.
Anda boleh melihat bahawa baris sebelum ke-16 dipadamkan.
4.1.4 Gunakan perpustakaan TA-Lib untuk menjana nilai RSI penunjuk kekuatan relatif
Nilai RSI boleh mencerminkan kekuatan pertumbuhan harga saham berbanding penurunan dalam jangka pendek
, membantu kami membuat pertimbangan yang lebih baik Trend kenaikan dan penurunan harga saham. Semakin besar nilai RSI, semakin kukuh aliran menaik berbanding aliran menurun, dan sebaliknya, aliran menaik yang lemah adalah relatif kepada aliran menurun. Formula pengiraan nilai RSI adalah seperti berikut. Contoh: Menurut data dalam jadual di atas, ambil N=6 , boleh didapati bahawa harga kenaikan purata 6 hari ialah (2+2+2)/6=1, dan harga kejatuhan purata 6 hari ialah (1+1+1)/6=0.5 , jadi nilai RSI ialah (1/(1+0.5))×100=66.7. Biasanya nilai RSI adalah antara 20 dan 80. Jika melebihi 80, ia terlebih beli, jika di bawah 20, ia terlebih jual Jika ia bersamaan dengan 50, ia dianggap begitu kuasa pembeli dan penjual adalah sama. Sebagai contoh, jika harga saham meningkat selama 6 hari berturut-turut, purata harga jatuh pada hari ke-6 akan menjadi 0, dan nilai RSI pada hari ke-6 akan menjadi 100. Ini menunjukkan bahawa pembeli saham berada dalam kedudukan yang sangat kukuh pada kali ini, tetapi pelabur juga diingatkan untuk berhati-hati bahawa ini juga mungkin tempoh yang berlebihan Dalam keadaan membeli, anda perlu mengelakkan risiko kejatuhan harga saham. Nilai MOM penunjuk momentum boleh dijana melalui kod berikut. MOM ialah singkatan momentum, yang mencerminkan kadar kenaikan dan penurunan harga saham dalam tempoh masa , formula pengiraan seperti berikut. Contoh: Katakan anda ingin mengira nilai MOM bagi No 6, Dalam kod sebelumnya, tempoh masa parameter ditetapkan kepada 5, maka anda perlu menolak harga penutup No 1 daripada harga penutup No 6, iaitu nilai MOM No 6 ialah 2.2 -1.2=1 Begitu juga, nilai MOM No. 7 ialah 2.4-1.4=1. Menghubungkan nilai MOM untuk hari berturut-turut membentuk keluk yang mencerminkan kenaikan dan kejatuhan harga saham. Anda boleh menjana purata pergerakan eksponen EMA melalui kod berikut. EMA ialah purata bergerak wajaran yang menurun secara eksponen, yang dianalisis berdasarkan hasil pengiraan digunakan untuk menilai perubahan pada masa hadapan trend harga saham. Formula pengiraan EMA adalah seperti berikut. Antaranya, EMAtoday ialah nilai EMA hari ini; EMA semalam ialah nilai EMA; indeks pelicinan, secara amnya Nilai ialah 2/(N+1), N mewakili bilangan hari, apabila N ialah 6, α ialah 2/7, dan EMA yang sepadan dipanggil EMA6, iaitu pergerakan eksponen 6 hari purata. Formula terus berulang sehingga nilai EMA pertama muncul (nilai EMA pertama biasanya purata lima nombor pertama). Contoh: EMA6 Nilai EMA pertama ialah purata 5 nombor pertama, jadi tiada nilai EMA dalam 5 pertama hari; Nilai EMA pada No. 6 ialah nilai EMA pertama, iaitu purata lima hari sebelumnya, iaitu, 1 nilai EMA pada No. 7 ialah nilai EMA kedua. Kod berikut boleh digunakan untuk menjana nilai MACD Moving Average Convergence dan Divergence. MACD ialah penunjuk yang biasa digunakan dalam pasaran saham Ia adalah pembolehubah derivatif berdasarkan nilai EMA. Pembaca yang berminat boleh belajar. Di sini anda hanya perlu tahu bahawa MACD ialah penunjuk arah aliran, dan perubahannya mewakili perubahan dalam arah aliran pasaran MACD pada tahap K-line yang berbeza mewakili arah aliran belian dan jualan dalam kitaran tahap semasa. 首先强调最核心的一点:应该是用当天的股价数据预测下一天的股价涨跌情况,所以目标变量y应该是下一天的股价涨跌情况。为什么是用当天的股价数据预测下一天的股价涨跌情况呢?这是因为特征变量中的很多数据只有在当天交易结束后才能确定(例如,收盘价close只有收盘了才有),所以当天正在交易时的股价涨跌情况是无法预测的,而等到收盘时尽管所需数据齐备,但是当天的股价涨跌情况已成定局,也就没有必要预测了,所以是用当天的股价数据预测下一天的股价涨跌情况。 第2行代码中使用了NumPy库中的where()函数,传入的3个参数的含义分别为判断条件、满足条件的赋值、不满足条件的赋值。其中df['price_change'].shift(-1)是利用shift()函数将price_change(股价变化)这一列的所有数据向上移动1行,这样就获得了每一行对应的下一天的股价变化。因此,这里的判断条件就是下一天的股价变化是否大于0,如果大于0,说明下一天股价涨了,则y赋值为1;如果不大于0,说明下一天股价不变或跌了,则y赋值为-1。预测结果就只有1或-1两种分类。 这里需要注意的是,划分要按照时间序列进行,而不能用train_test_split()函数进行随机划分。这是因为股价的变化趋势具有时间性特征,而随机划分会破坏这种特征,所以需要根据当天的股价数据预测下一天的股价涨跌情况,而不能根据任意一天的股价数据预测下一天的股价涨跌情况。 将前90%的数据作为训练集,后10%的数据作为测试集,代码如下。 设置模型参数:决策树的最大深度max_depth设置为3,即每个决策树最多只有3层;弱学习器(即决策树模型)的个数n_estimators设置为10,即该随机森林中共有10个决策树;叶子节点的最小样本数min_samples_leaf设置为10,即如果叶子节点的样本数小于10则停止分裂;随机状态参数random_state的作用是使每次运行结果保持一致,这里设置的数字123没有特殊含义,可以换成其他数字。 用predict_proba()函数可以预测属于各个分类的概率,代码如下。 通过如下代码可以查看整体的预测准确度。 打印输出score为0.40,说明模型对整个测试集中约40%的数据预测正确。这一预测准确度并不算高,也的确符合股票市场千变万化的特点。 通过如下代码可以分析各个特征变量的特征重要性。 由图可知,当日收盘价close、MA5、MACDhist相关指标等特征变量对下一天股价涨跌结果的预测准确度影响较大。 前面已经评估了模型的预测准确度,不过在商业实战中,更关心它的收益回测曲线(又称为净值曲线),也就是看根据搭建的模型获得的结果是否比不利用模型获得的结果更好。 可视化结果如下图所示。图中上方的曲线为根据模型得到的收益率曲线,下方的曲线为股票本身的收益率曲线,可以看到,利用模型得到的收益还是不错的。 要说明的是,这里讲解的量化金融内容比较浅显,搭建的模型过于理想化,真正的股市是错综复杂的,股票交易也有很多限制,如不能做空、不能T+0交易,还要考虑手续费等因素。 随机森林模型是一种非常重要的集成模型,它集成了决策树模型的众多优点,又规避了决策树模型容易过度拟合等缺点,在实战中应用较为广泛。 【相关推荐:Python3视频教程 】
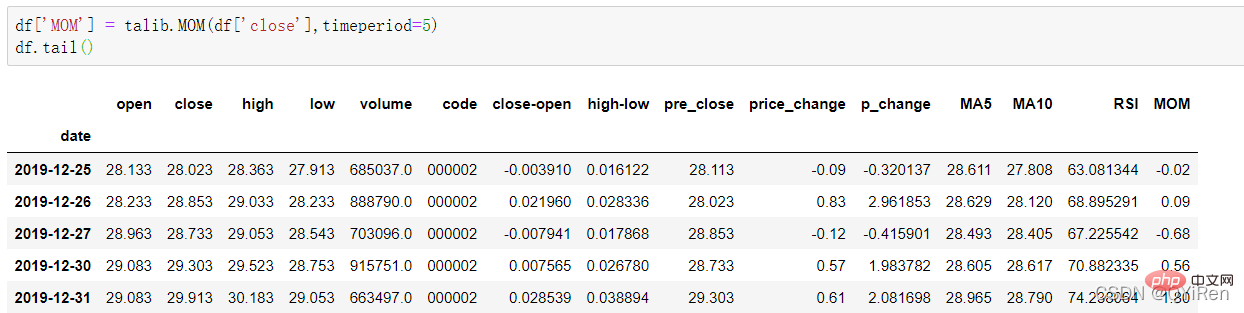
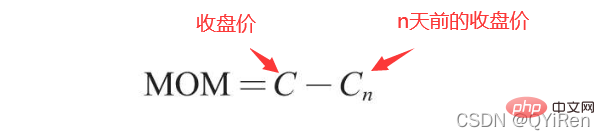
4.1.5 Gunakan perpustakaan TA-Lib untuk menjana nilai MOM penunjuk momentum

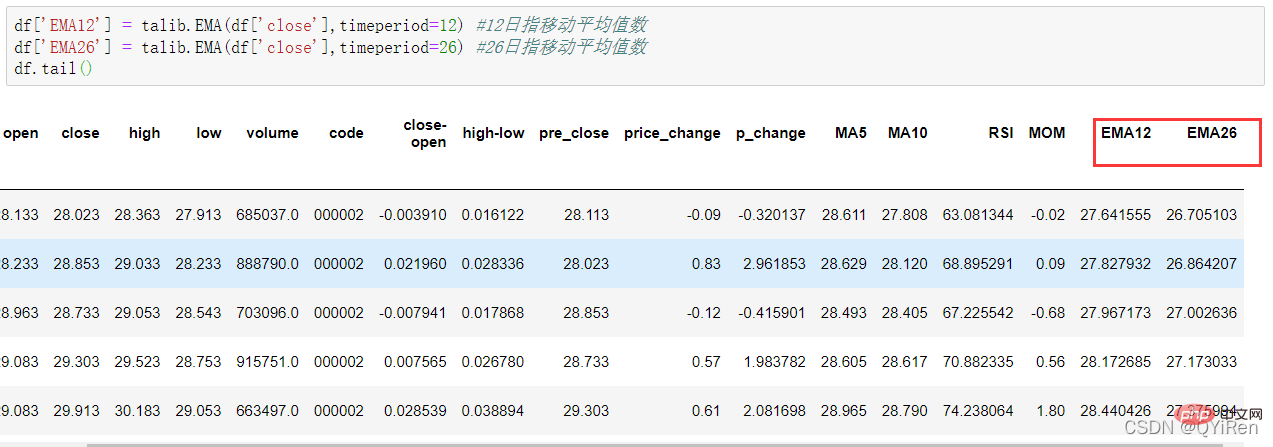
4.1.6 Gunakan perpustakaan TA-Lib untuk menjana purata pergerakan eksponen EMA
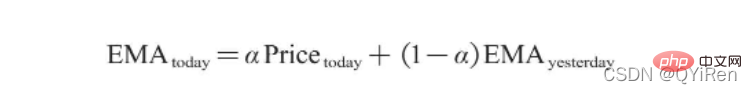

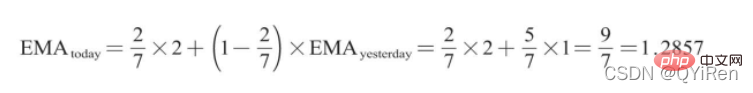
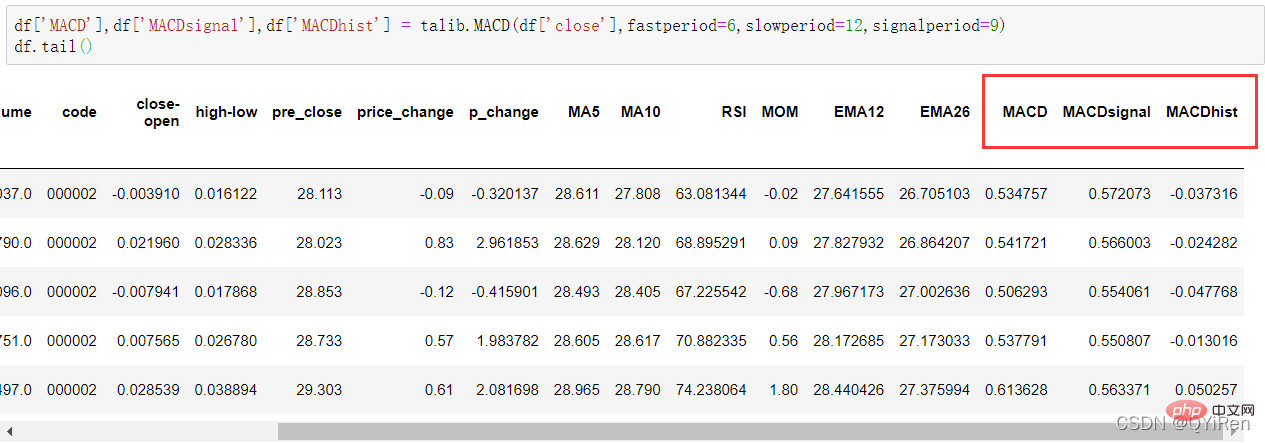
4.1.7 Gunakan perpustakaan TA-Lib untuk menjana nilai MACD Moving Average Convergence dan Divergence
4.2 模型搭建
4.2.1 引入需要搭建的库
# 导入相关库
import tushare as ts
import numpy as np
import pandas as pd
import talib
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score
4.2.2 获取数据
# 1.股票基本数据获取
import tushare as ts
df = ts.get_k_data('000002',start='2015-01-01',end='2019-12-31')
df = df.set_index('date')
# 2.简单衍生变量数据构造
df['close-open'] = (df['close'] - df['open']) / df['open']
df['high-low'] = (df['high'] - df['low']) / df['low']
df['pre_close'] = df['close'].shift(1)
df['price_change'] = df['close'] - df['pre_close']
df['p_change'] = (df['close'] - df['pre_close']) / df['pre_close'] * 100
# 3.移动平均线相关数据构造
df['MA5'] = df['close'].rolling(5).mean()
df['MA10'] = df['close'].rolling(10).mean()
df.dropna(inplace=True)
# 4.通过TA-Lib库构造衍生变量数据
df['RSI'] = talib.RSI(df['close'],timeperiod=12)
df['MOM'] = talib.MOM(df['close'],timeperiod=5)
df['EMA12'] = talib.EMA(df['close'],timeperiod=12) #12日指移动平均值数
df['EMA26'] = talib.EMA(df['close'],timeperiod=26) #26日指移动平均值数
df['MACD'],df['MACDsignal'],df['MACDhist'] = talib.MACD(df['close'],fastperiod=6,slowperiod=12,signalperiod=9)
df.dropna(inplace=True)4.2.3 提取特征变量和目标变量
X = df[['close','volume','close-open','MA5','MA10','high-low','RSI','MOM','EMA12','MACD','MACDsignal','MACDhist']]
y = np.where(df['price_change'].shift(-1) > 0,1,-1)
4.2.4 划分训练集和测试集
X_length = X.shape[0]
split = int(X_length * 0.9)
X_train,X_test = X[:split],X[split:]
y_train,y_test = y[:split],y[split:]
4.2.5 模型搭建
model = RandomForestClassifier(max_depth=3,n_estimators=10,min_samples_leaf=10,random_state=123)
model.fit(X_train,y_train)
4.3 模型评估与使用
4.3.1 预测下一天的股价涨跌情况
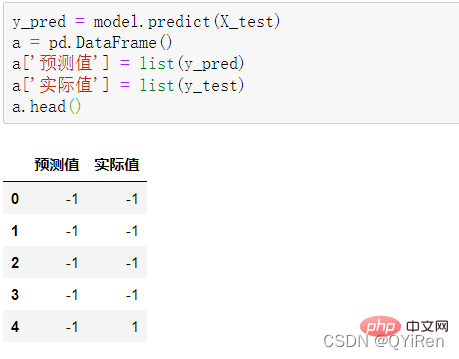
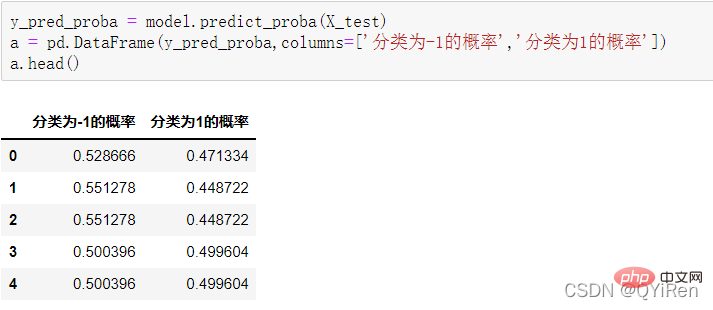
4.3.2 模型准确度评估
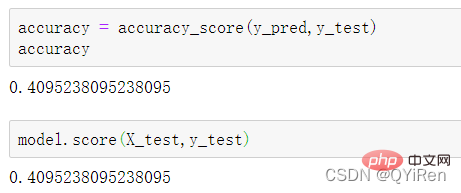
4.3.3 分析特征变量的特征重要性
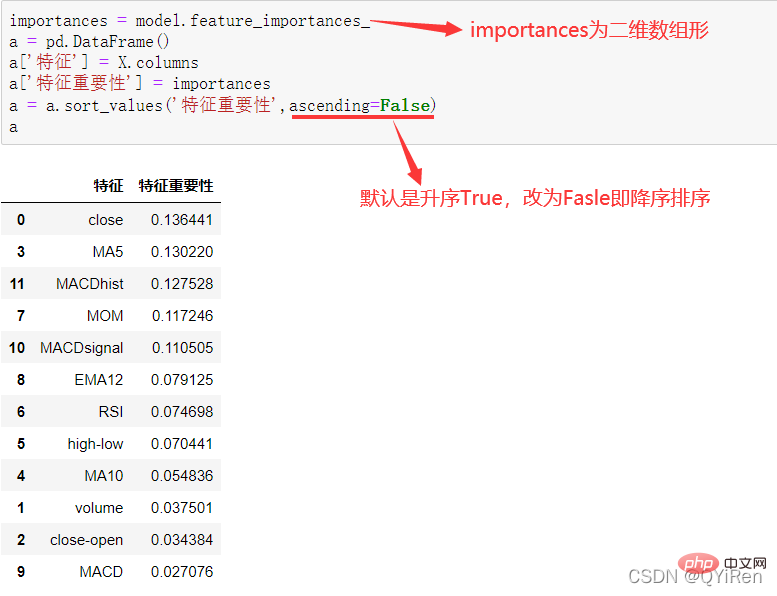
4.4 参数调优
from sklearn.model_selection import GridSearchCV
parameters={'n_estimators':[5,10,20],'max_depth':[2,3,4,5,6],'min_samples_leaf':[5,10,20,30]}
new_model = RandomForestClassifier(random_state=123)
grid_search = GridSearchCV(new_model,parameters,cv=6,scoring='accuracy')
grid_search.fit(X_train,y_train)
grid_search.best_params_
# 输出
# {'max_depth': 5, 'min_samples_leaf': 20, 'n_estimators': 5} 4.5 收益回测曲线绘制
# 在测试数据上添加一列,预测收益
X_test['prediction'] = model.predict(X_test)
# 计算每天的股价变化率
X_test['p_change'] = (X_test['close'] - X_test['close'].shift(1)) / X_test['close'].shift(1)
# 计算累积收益率
# 例如,初始股价是1,2天内的价格变化率为10%
# 那么用cumprod()函数可以求得2天后的股价为1×(1+10%)×(1+10%)=1.21
# 此结果也表明2天的收益率为21%。
X_test['origin'] = (X_test['p_change'] + 1).cumprod()
# 计算利用模型预测后的收益率
X_test['strategy'] = (X_test['prediction'].shift(1) * X_test['p_change'] + 1).cumprod()
X_test[['strategy','origin']].dropna().plot()
# 设置自动倾斜
plt.gcf().autofmt_xdate()
plt.show()
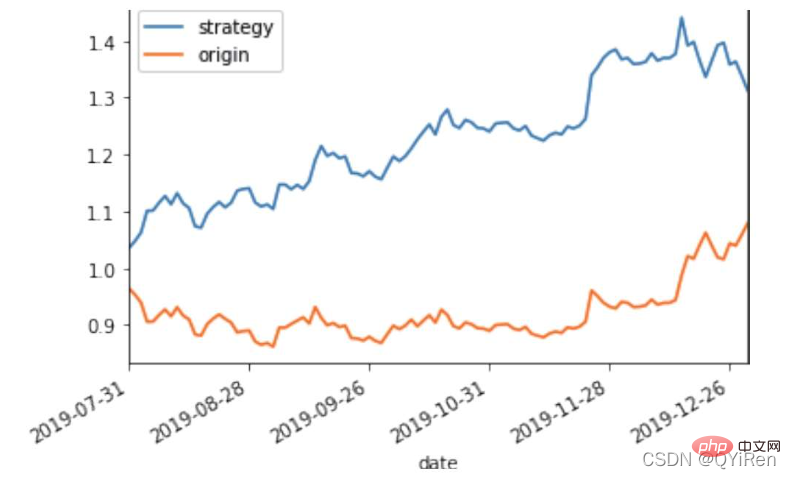
Atas ialah kandungan terperinci Penjelasan terperinci tentang contoh model hutan rawak Python. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!