Prinsip dan pelaksanaan algoritma Perdana dalam Java (perkongsian ringkasan)-javaTutorial-php.cn

Artikel ini membawa anda pengetahuan yang berkaitan tentang java Algoritma Prime ialah algoritma carian yang lengkap untuk membina pepohon rentang minimum daripada graf yang disambungkan. Artikel ini terutamanya memperkenalkan prinsip dan pelaksanaan algoritma Perdana dalam Java Jika anda berminat, anda boleh mempelajarinya.

Prinsip dan pelaksanaan algoritma Perdana dalam Java (perkongsian ringkasan)

Pembelajaran yang disyorkan: "tutorial video java"

Pengenalan kepada algoritma Prim

1

Dalam proses spanning tree, nod yang sudah ada dalam spanning tree dianggap sebagai satu set, nod selebihnya dianggap sebagai set lain, dan tepi dengan berat terkecil dipilih daripada tepi yang menghubungkan kedua-dua set, iaitu, Boleh.

2. Pengenalan Algoritma

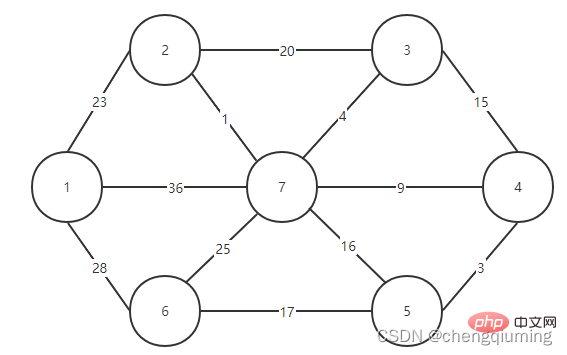
Mula-mula pilih nod, seperti nod 1, dan letakkan dalam set U, U={1}, kemudian Nod yang tinggal ialah V-U={2,3,4,5,6,7}, dan set V ialah set semua nod graf.

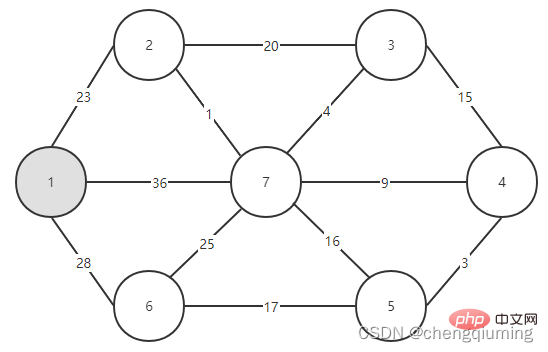
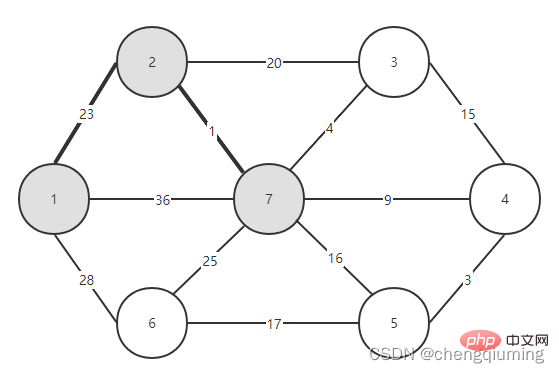
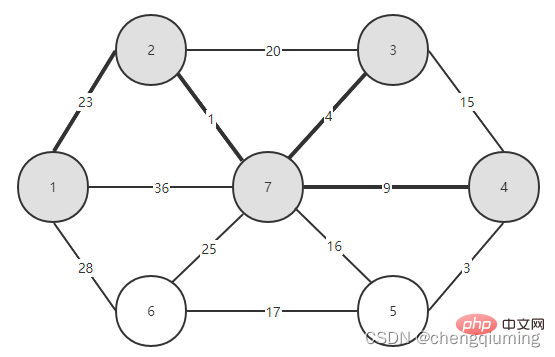
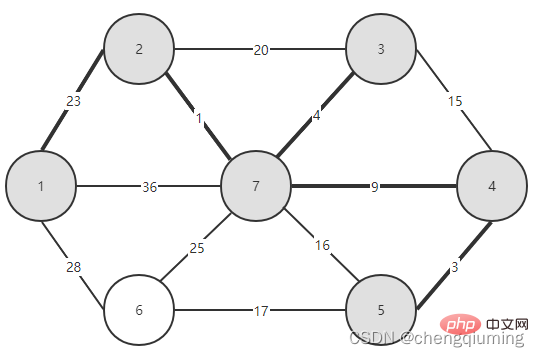
Kini anda hanya perlu melihat tepi mana yang mempunyai berat terkecil antara tepi yang menghubungkan dua set (U dan V-U), dan kaitkan nod dengan tepi terkecil Sertai tetapkan U. Seperti yang dapat dilihat daripada rajah di atas, antara 3 tepi yang menghubungkan dua set, tepi 1-2 mempunyai berat terkecil Pilihnya dan tambah nod 2 pada set U, U={1,2}, V - U= { 3,4,5,6}, seperti yang ditunjukkan dalam rajah di bawah.

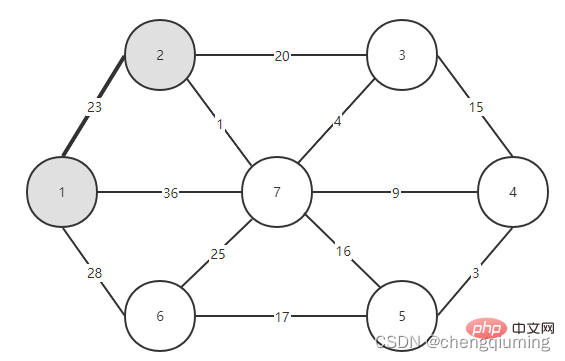
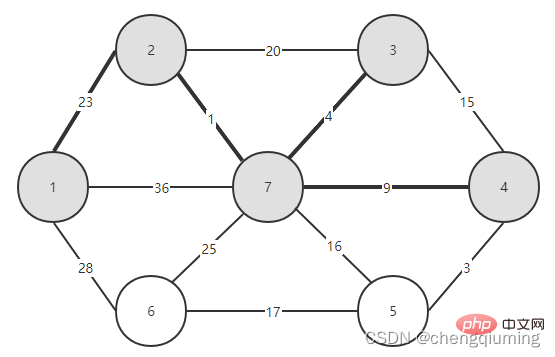
Kemudian pilih tepi dengan berat terkecil daripada tepi yang menyambungkan dua set (U dan V-U). Seperti yang dapat dilihat dari rajah di atas, antara empat tepi yang menghubungkan dua set, berat tepi dari nod 2 ke nod 7 adalah yang paling kecil Pilih tepi ini dan tambah nod 7 pada set U={1,2,7} , V-U ={3,4,5,6}.

Ini berterusan sehingga U=V tamat, dan graf yang terdiri daripada tepi yang dipilih dan semua nod ialah pokok rentang minimum. Ini adalah algoritma Prim.

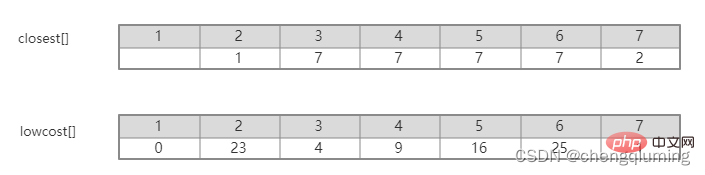
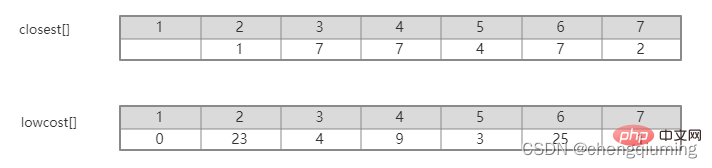
Melihat graf secara intuitif, adalah mudah untuk mengetahui tepi mana dari set U ke set U-V yang mempunyai berat terkecil Namun, ia memakan masa untuk menyenaraikan tepi ini secara menyeluruh dan kemudian cari nilai minimum Darjahnya terlalu tinggi. Masalah ini boleh diselesaikan dengan bijak dengan menetapkan tatasusunan Closet[j] mewakili titik jiran terdekat dari nod j dalam set V-U hingga set U. Kos rendah[j] mewakili nilai tepi dari nod j dalam set V-U ke titik jiran terdekat dalam. set U. Iaitu, berat tepi (j, paling hampir[j]).

Sebagai contoh, dalam rajah di atas, titik jiran terdekat dari nod 7 ke set U ialah 2, paling hampir[7]=2. Nilai tepi dari nod 7 ke titik jiran terdekat 2 ialah 1, iaitu berat tepi (2,7), direkodkan sebagai kos rendah[7]=1, seperti yang ditunjukkan dalam rajah di bawah.

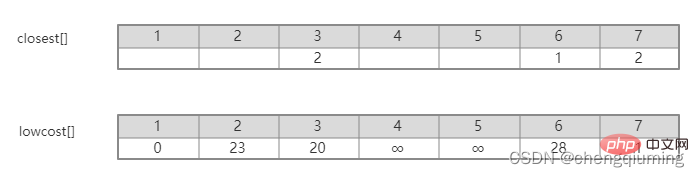
Jadi cari nod[] kos rendah terendah dalam set V - U.

3. Langkah-langkah algoritma

1. Permulaan

Biar set U={u0}, u0 milik V dan mulakan tatasusunan yang paling hampir[], kos rendah[] dan s[].

2. Cari nod t dengan nilai kos rendah terkecil dalam set V-U, iaitu kos rendah[t]=min{kos rendah[j]}, j tergolong dalam V-U Nod t yang memenuhi formula ini ialah sambungan U dalam set V-U titik terdekat.

3. Tambahkan nod t pada set U.

4 Jika set V - U kosong, algoritma tamat, jika tidak pergi ke langkah 5.

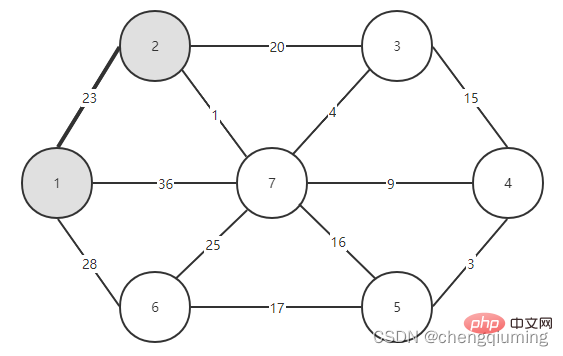
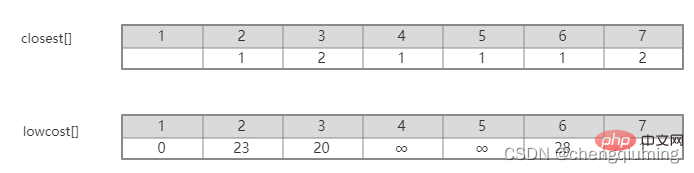
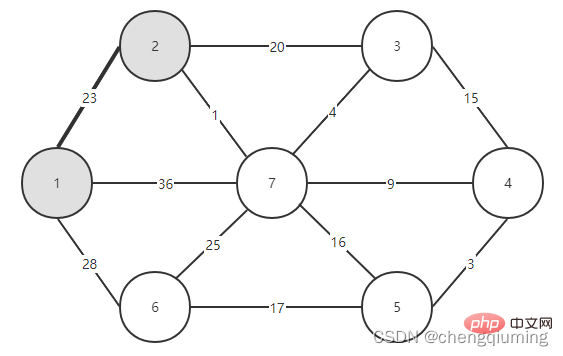
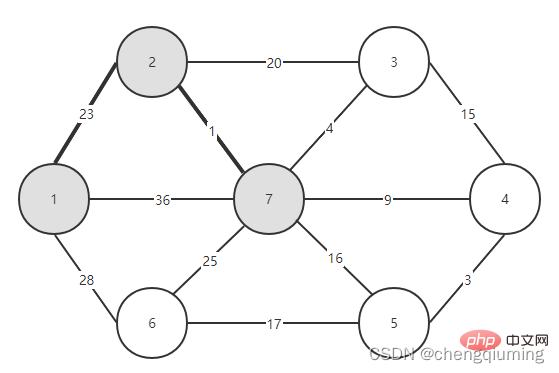
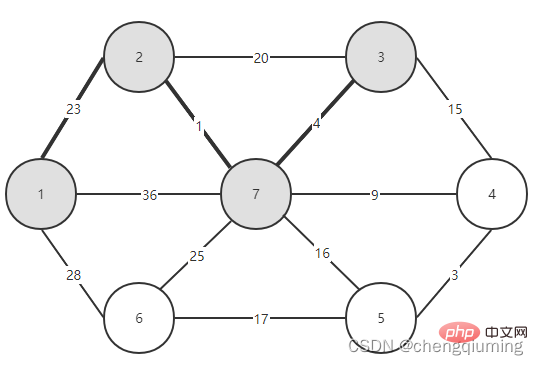
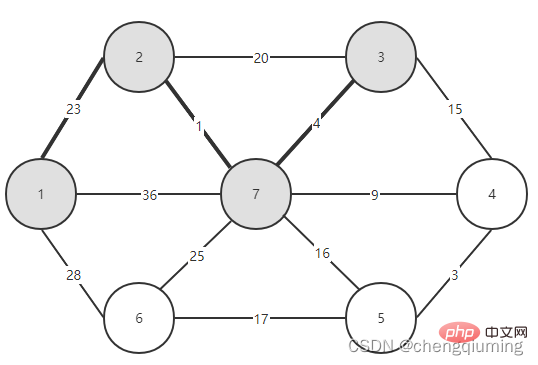
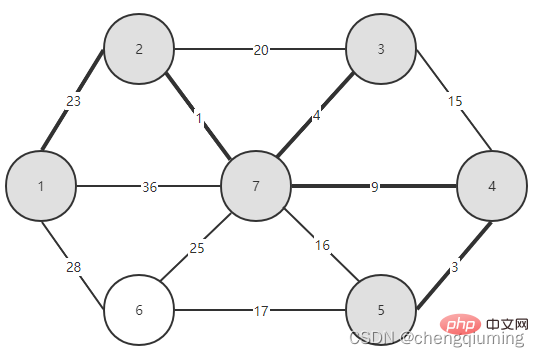
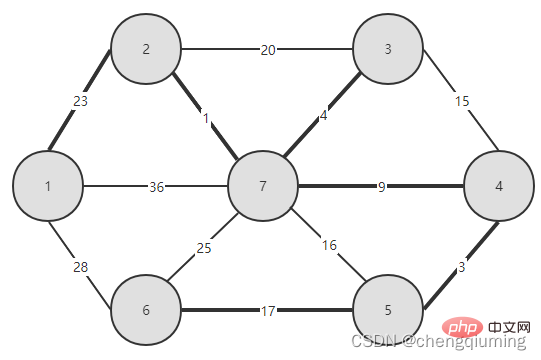
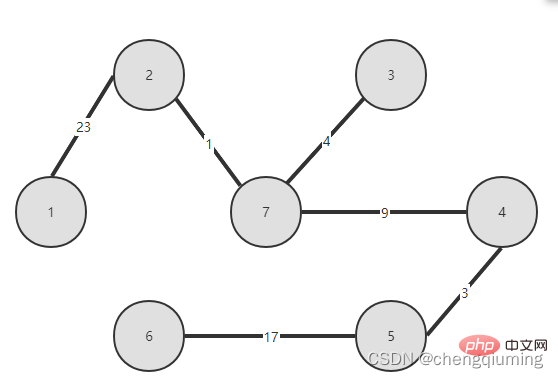
5. Kemas kini kos rendah[] dan paling hampir[] untuk semua nod j dalam set V-U. jika(C[t][j]

Ikuti langkah di atas, dan akhirnya anda boleh mendapatkan pokok rentang dengan jumlah pemberat terkecil.

4. Gambar rajah

Graf G=(V,E) ialah graf wajaran bersambung tidak berarah, seperti yang ditunjukkan dalam rajah di bawah.

1 Permulaan. Andaikan u0=1, biarkan set U={1}, set V-U={2,3,4,5,6,7}, s[1]=true, mulakan tatasusunan yang paling hampir[]: kecuali nod 1, semua nod lain ialah 1, yang bermaksud bahawa titik jiran terdekat dari nod dalam set V-U kepada set U adalah semua 1.kos rendah[]: nilai tepi dari nod 1 ke nod dalam set V-U. terdekat[] dan kos rendah[] ditunjukkan dalam rajah di bawah.

Gambar selepas pemula ialah:

2 Cari nod dengan kos rendah terkecil, sepadan dengan t=2 Tepi dan nod yang dipilih adalah seperti yang ditunjukkan di bawah.

3 Tambahkan pada set U. Tambahkan nod t pada set U, U={1,2} dan kemas kini V-U={3,4,5,6,7}

4 pada masa yang sama. Bagi setiap titik j yang bersebelahan bagi t dalam set V-U, ia boleh dikemas kini dengan bantuan t. Titik bersebelahan nod 2 ialah nod 3 dan nod 7.

C[2][3]=20

C [2][7]=1

kemas kini paling hampir[] dan kos rendah[] seperti yang ditunjukkan di bawah.

Set yang dikemas kini adalah seperti yang ditunjukkan di bawah:

5 Cari nod dengan kos rendah terkecil, sepadan t= 7. Tepi dan nod yang dipilih adalah seperti yang ditunjukkan di bawah.

6 Tambahkan pada set U. Tambahkan nod t pada set U, U={1,2,7} dan kemas kini V-U={3,4,5,6}

7 pada masa yang sama. Bagi setiap titik j yang bersebelahan bagi t dalam set V-U, ia boleh dikemas kini dengan bantuan t. Titik bersebelahan nod 7 ialah nod 3, 4, 5, dan 6.

C[7][3]=4
C[7][4]=4
C[7 ][ 5]=4
C[7][6]=4< ;kos rendah[ 6]=28, kemas kini jarak jiran terdekat kos rendah[3]=25, jiran terdekat terdekat[6]=7;

Terhampir[] dan kos rendah[] yang dikemas kini adalah seperti ditunjukkan di bawah.

Set yang dikemas kini adalah seperti yang ditunjukkan di bawah:

8 Cari nod dengan kos rendah terkecil, sepadan t= 3. Tepi dan nod yang dipilih adalah seperti yang ditunjukkan di bawah.

9 Tambahkan pada set U. Tambahkan nod t pada set U, U={1,2,3,7} dan kemas kini V-U={4,5,6}

10 kemas kini pada masa yang sama. Bagi setiap titik j yang bersebelahan bagi t dalam set V-U, ia boleh dikemas kini dengan bantuan t. Jiran nod 3 ialah nod 4.

C[3][4]=15>kos rendah[4]=9, tatasusunan

terhampir[] dan kos rendah[] tidak dikemas kini tidak berubah.

Set yang dikemas kini adalah seperti yang ditunjukkan di bawah:

11 Cari nod dengan kos rendah terkecil, sepadan t=4, dan tepi serta nod yang dipilih ialah seperti yang ditunjukkan di bawah.

12 ditambahkan pada set U. Tambahkan nod t pada set U, U={1,2,3,4,7} dan kemas kini V-U={5,6}

13 pada masa yang sama. Bagi setiap titik j yang bersebelahan bagi t dalam set V-U, ia boleh dikemas kini dengan bantuan t. Jiran nod 4 ialah nod 5.

C[4][5]=3

dikemas kini paling hampir [] dan kos rendah[] ditunjukkan dalam rajah di bawah.

Set yang dikemas kini adalah seperti yang ditunjukkan di bawah:

14 Cari nod dengan kos rendah terkecil, sepadan t= 5. Tepi dan nod yang dipilih adalah seperti yang ditunjukkan di bawah.

15 ditambah pada set U. Tambahkan nod t pada set U, U={1,2,3,4,5,7} dan kemas kini V-U={6}

16 kemas kini pada masa yang sama. Bagi setiap titik j yang bersebelahan bagi t dalam set V-U, ia boleh dikemas kini dengan bantuan t. Jiran nod 5 ialah nod 6.

C[5][6]=17

Dikemas kini Set ialah seperti yang ditunjukkan di bawah:

17 Cari nod dengan kos rendah terkecil, sepadan dengan t=6, dan tepi serta nod yang dipilih adalah seperti yang ditunjukkan di bawah.

18 ditambah pada set U. Tambahkan nod t pada set U, U={1,2,3,4,5,6,7} dan kemas kini V-U={}

19 pada masa yang sama. Bagi setiap titik j yang bersebelahan bagi t dalam set V-U, ia boleh dikemas kini dengan bantuan t. Nod 6 tidak mempunyai titik bersebelahan dalam set V-U. Tidak perlu mengemas kini[] dan kos rendah[].

20 Pokok rentang minimum yang diperolehi adalah seperti berikut. Jumlah pemberat bagi pokok rentang minimum ialah 57.

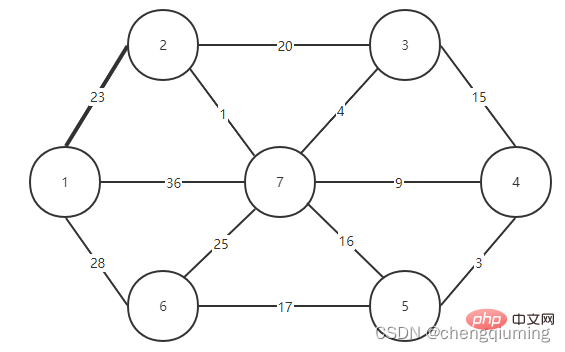
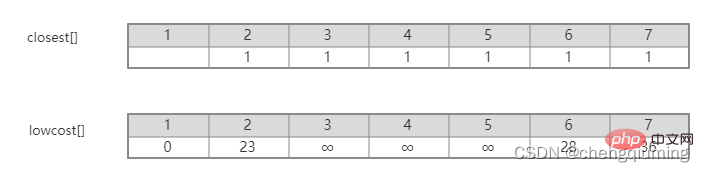
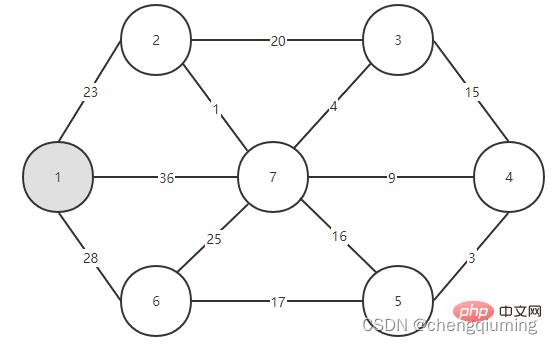
Pelaksanaan algoritma perdana

1. Graf yang dibina

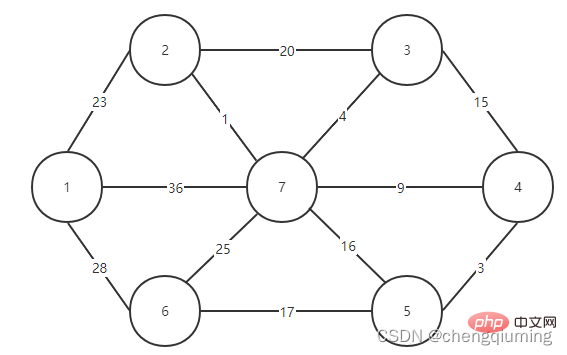
2. Kod

package graph.prim;
 
import java.util.Scanner;
 
public class Prim {
    static final int INF = 0x3f3f3f3f;
    static final int N = 100;
    // 如果s[i]=true,说明顶点i已加入U
    static boolean s[] = new boolean[N];
    static int c[][] = new int[N][N];
    static int closest[] = new int[N];
    static int lowcost[] = new int[N];
 
    static void Prim(int n) {
        // 初始时，集合中 U 只有一个元素，即顶点 1
        s[1] = true;
        for (int i = 1; i <= n; i++) {
            if (i != 1) {
                lowcost[i] = c[1][i];
                closest[i] = 1;
                s[i] = false;
            } else
                lowcost[i] = 0;
        }
        for (int i = 1; i < n; i++) {
            int temp = INF;
            int t = 1;
            // 在集合中 V-u 中寻找距离集合U最近的顶点t
            for (int j = 1; j <= n; j++) {
                if (!s[j] && lowcost[j] < temp) {
                    t = j;
                    temp = lowcost[j];
                }
            }
            if (t == 1)
                break; // 找不到 t，跳出循环
            s[t] = true; // 否则，t 加入集合U
            for (int j = 1; j <= n; j++) { // 更新 lowcost 和 closest
                if (!s[j] && c[t][j] < lowcost[j]) {
                    lowcost[j] = c[t][j];
                    closest[j] = t;
                }
            }
        }
    }
 
    public static void main(String[] args) {
        int n, m, u, v, w;
        Scanner scanner = new Scanner(System.in);
        n = scanner.nextInt();
        m = scanner.nextInt();
        int sumcost = 0;
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= n; j++)
                c[i][j] = INF;
        for (int i = 1; i <= m; i++) {
            u = scanner.nextInt();
            v = scanner.nextInt();
            w = scanner.nextInt();
            c[u][v] = c[v][u] = w;
        }
        Prim(n);
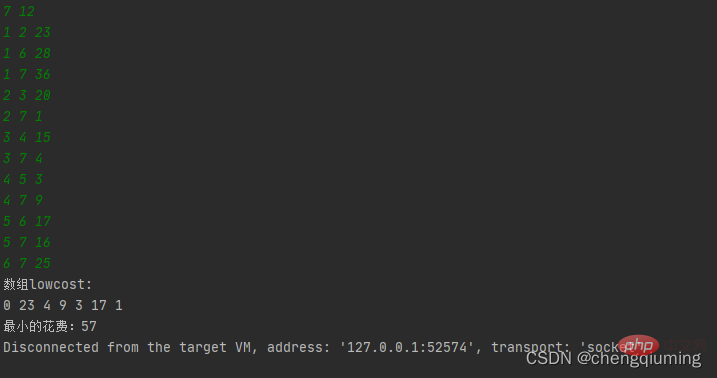
        System.out.println("数组lowcost:");
 
        for (int i = 1; i <= n; i++)
            System.out.print(lowcost[i] + " ");
 
        System.out.println();
        for (int i = 1; i <= n; i++)
            sumcost += lowcost[i];
        System.out.println("最小的花费：" + sumcost);
    }
}

Salin selepas log masuk

3.

tutorial video java

》

Atas ialah kandungan terperinci Prinsip dan pelaksanaan algoritma Perdana dalam Java (perkongsian ringkasan). Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!