Fahami algoritma Vue Diff dalam satu artikel-View.js-php.cn

Artikel ini membawakan anda pengetahuan yang berkaitan tentang vue, yang terutamanya memperkenalkan isu berkaitan tentang algoritma diff Fungsi algoritma diff adalah untuk mencari perbezaan antara dua set nod vdom nod sebanyak mungkin supaya operasi kemas kini dapat diselesaikan dengan penggunaan prestasi yang minimum Mari kita lihat bersama-sama.

Fahami algoritma Vue Diff dalam satu artikel

[Cadangan berkaitan: tutorial video javascript, tutorial vue.js]

Mengapa Perlu algoritma berbeza?

Untuk bekas (seperti #app yang biasa kami gunakan), kandungannya biasanya mempunyai tiga situasi:

Jenis rentetan, iaitu teks .
tatasusunan nod anak, iaitu, ia mengandungi satu atau lebih nod anak
null, iaitu tiada nod anak

Dalam vue, elemen dom akan diproses sebagai vdom Atribut HTML dan pengikatan peristiwa kami akan diproses pada vdom, dan akhirnya dijadikan dom sebenar.

Virtual Dom: Objek JavaScript yang digunakan untuk menerangkan nod dom sebenar.

Sebab penggunaan vdom ialah jika setiap operasi dilakukan terus pada dom sebenar, ia akan menyebabkan banyak overhead. Apabila menggunakan vdom, penggunaan prestasi boleh dikurangkan daripada tahap operasi dom sebenar kepada tahap JavaScript, yang secara relatifnya lebih baik. Vdom mudah adalah seperti berikut:

const vdom = {
    type:"div",
    props:{
        class: "class",
        onClick: () => { console.log("click") }
    },
    children: [] // 简单理解这就是上述三种内容
}

Salin selepas log masuk

Untuk kemas kini nod vue, vdom digunakan untuk perbandingan.

Algoritma perbezaan ialah kes kedua yang digunakan untuk kandungan kontena. Apabila kandungan dalam bekas sebelum mengemas kini ialah satu set nod anak, dan kandungan selepas mengemas kini masih merupakan satu set nod. Jika algoritma diff tidak digunakan, operasi paling mudah ialah menyahpasang semua DOM sebelumnya dan kemudian melekapkan semua nod baharu semasa.

Tetapi mengendalikan objek dom secara langsung adalah sangat intensif prestasi, jadi peranan algoritma diff adalah untuk mencari perbezaan antara dua set nod vdom dan menggunakan semula nod dom sebanyak mungkin untuk meminimumkan penggunaan prestasi. Selesaikan operasi kemas kini.

Seterusnya, mari kita bincangkan tentang tiga algoritma perbezaan, bermula daripada mudah kepada kompleks.

Algoritma Beza Mudah

Mengapa anda memerlukan kunci?

Seterusnya, kami akan menerangkan mengapa kunci diperlukan melalui dua situasi?

Jika terdapat dua set tatasusunan nod lama dan baharu seperti berikut:

const oldChildren = [
    {type: &#39;p&#39;},
    {type: &#39;span&#39;},
    {type: &#39;div&#39;},
]
const newChildren = [
    {type: &#39;div&#39;},
    {type: &#39;p&#39;},
    {type: &#39;span&#39;},
    {type: &#39;footer&#39;},
]

Salin selepas log masuk

Jika kita melakukan perbandingan biasa, langkahnya hendaklah seperti berikut:

Cari yang lebih pendek Sekumpulan perbandingan bulat

Teg p pertama tidak sepadan dengan teg div Anda perlu menyahpasang teg p dahulu dan kemudian memasang teg div.
Teg spam pertama tidak sepadan dengan teg p Anda perlu menyahpasang teg span dahulu dan kemudian memasang teg p.
Teg div pertama tidak sepadan dengan teg span Anda perlu menyahpasang teg div dahulu dan kemudian melekapkan teg span.
Pengaki label tambahan terakhir wujud dalam tatasusunan nod baharu, cuma lekapkannya.

Kemudian kami mendapati bahawa 7 operasi DOM telah dilakukan, tetapi tiga nama pertama boleh digunakan semula, tetapi kedudukan telah berubah. Jika kita menggunakan semula nod, kita perlu menentukan sama ada kedua-dua nod adalah sama, tetapi keadaan sedia ada semasa tidak dapat dipenuhi.

Jadi, kami perlu memperkenalkan kunci, yang bersamaan dengan nombor ID nod maya selagi jenis dan kunci kedua-dua nod maya adalah sama, kami menganggapnya sama dan boleh menggunakan semula DOM.

Pada masa ini, kita boleh mencari elemen yang digunakan semula dan menggerakkan dom, yang secara relatifnya lebih baik daripada sentiasa memasang dan memunggah nod.

Walau bagaimanapun, penggunaan semula dom tidak bermakna tidak perlu mengemas kini:

const oldVNode = {type: &#39;p&#39;, children: &#39;old&#39;, key: 1}
const newVNode = {type: &#39;p&#39;, children: &#39;new&#39;, key: 2}

Salin selepas log masuk

Nod di atas mempunyai jenis dan kunci yang sama, kami boleh menggunakannya semula dan hanya mengemas kini nod kanak-kanak pada masa ini.

Langkah algoritma perbezaan mudah

Mula-mula gunakan contoh untuk menggambarkan keseluruhan proses, dan kemudian terangkan kaedah

const oldChildren = [
    {type: &#39;p&#39;, children: &#39;p&#39;, key: 1},
    {type: &#39;span&#39;, children: &#39;span&#39;, key: 2},
    {type: &#39;div&#39;, children: &#39;div&#39;, key: 3},
    {type: &#39;section&#39;, children: &#39;section&#39;, key : 4},
]
const newChildren = [
    {type: &#39;div&#39;, children: &#39;new div&#39;, key: 3},
    {type: &#39;p&#39;, children: &#39;p&#39;, key: 1},
    {type: &#39;span&#39;, children: &#39;span&#39;, key: 2},
    {type: &#39;footer&#39;, children: &#39;footer&#39;, key: 5},
]

Salin selepas log masuk

Untuk memudahkan penerangan, label berbeza digunakan di sini. Keseluruhan proses adalah seperti berikut:

Fahami algoritma Vue Diff dalam satu artikel

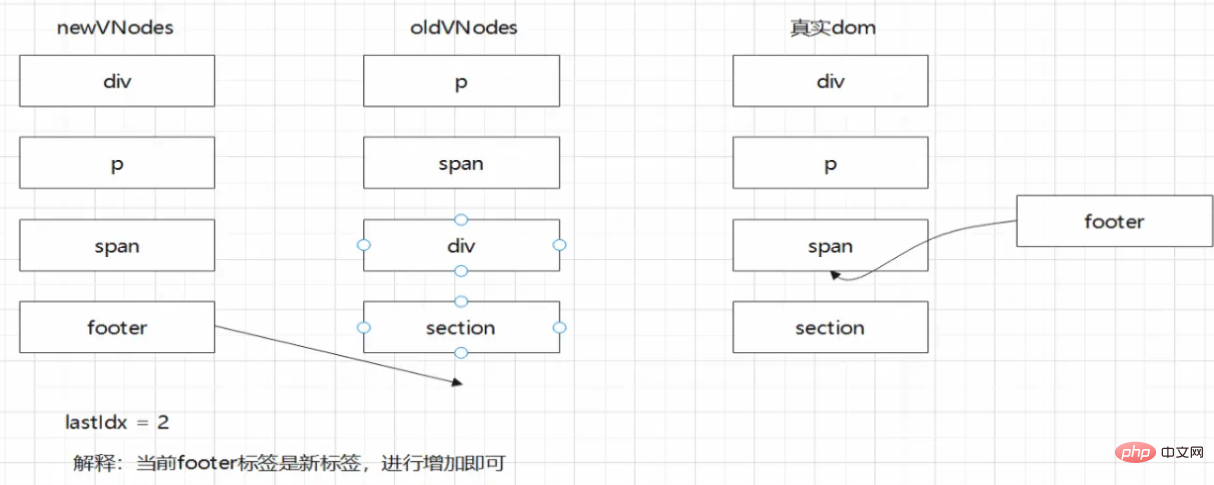
Mula melintasi dari tatasusunan nod baharu
Yang pertama ialah teg div, pada masa ini Subskrip bagi ialah 0, dan subskrip sebelumnya ialah 2. Kedudukan relatif tidak berubah, tiada pergerakan diperlukan, hanya kandungan nod yang perlu dikemas kini.
Yang kedua ialah tag p, subskrip semasa ialah 1 dan subskrip sebelumnya ialah 0. Dari segi kedudukan relatif, p telah berubah secara relatif kepada tag div dan perlu dialihkan. Kedudukan yang dialihkan adalah selepas tag div.
第三个是span标签，当前的下标是2，之前的下标是1。就相对位置而言，p相对于div标签有变化，需要进行移动。移动的位置就是在p标签之后。
第四个标签是footer，遍历旧节点数组发现并无匹配的元素。代表当前的元素是新节点，将其插入，插入的位置是span标签之后。
最后一步，遍历旧节点数组，并去新节点数组中查找是否有对应的节点，没有则卸载当前的元素。

如何找到需要移动的元素？

上述声明了一个lastIdx变量，其初始值为0。作用是保存在新节点数组中，对于已经遍历了的新节点在旧节点数组的最大的下标。那么对于后续的新节点来说，只要它在旧节点数组中的下标的值小于当前的lastIdx，代表当前的节点相对位置发生了改变，则需要移动，

举个例子：div在旧节点数组中的位置为2，大于当前的lastIdx，更新其值为2。对于span标签，它的旧节点数组位置为1，其值更小。又因为当前在新节点数组中处于div标签之后，就是相对位置发生了变化，便需要移动。

当然，lastIdx需要动态维护。

总结

简单diff算法便是拿新节点数组中的节点去旧节点数组中查找，通过key来判断是否可以复用。并记录当前的lastIdx，以此来判断节点间的相对位置是否发生变化，如果变化，需要进行移动。

双端diff算法

简单diff算法并不是最优秀的，它是通过双重循环来遍历找到相同key的节点。举个例子：

const oldChildren = [
    {type: &#39;p&#39;, children: &#39;p&#39;, key: 1},
    {type: &#39;span&#39;, children: &#39;span&#39;, key: 2},
    {type: &#39;div&#39;, children: &#39;div&#39;, key: 3},
]
const newChildren = [
    {type: &#39;div&#39;, children: &#39;new div&#39;, key: 3},
    {type: &#39;p&#39;, children: &#39;p&#39;, key: 1},
    {type: &#39;span&#39;, children: &#39;span&#39;, key: 2},
]

Salin selepas log masuk

其实不难发现，我们只需要将div标签节点移动即可，即进行一次移动。不需要重复移动前两个标签也就是p、span标签。而简单diff算法的比较策略即是从头至尾的循环比较策略，具有一定的缺陷。

顾名思义，双端diff算法是一种同时对新旧两组子节点的两个端点进行比较的算法

Fahami algoritma Vue Diff dalam satu artikel

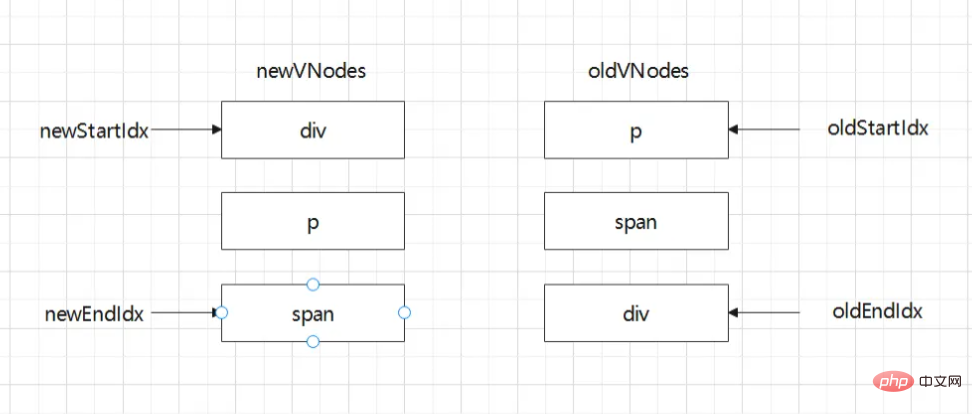
那么双端diff算法开始的步骤如下：

比较 oldStartIdx节点与 newStartIdx 节点，相同则复用并更新，否则
比较 oldEndIdx节点与 newEndIdx 节点，相同则复用并更新，否则
比较 oldStartIdx节点与 newEndIdx 节点，相同则复用并更新，否则
比较 oldEndIdx节点与 newStartIdx 节点，相同则复用并更新，否则

简单概括：

旧头 === 新头？复用，不需移动
旧尾 === 新尾？复用，不需移动
旧头 === 新尾？复用，需要移动
旧尾 === 新头？复用，需要移动

对于上述例子而言，比较步骤如下：

Fahami algoritma Vue Diff dalam satu artikel

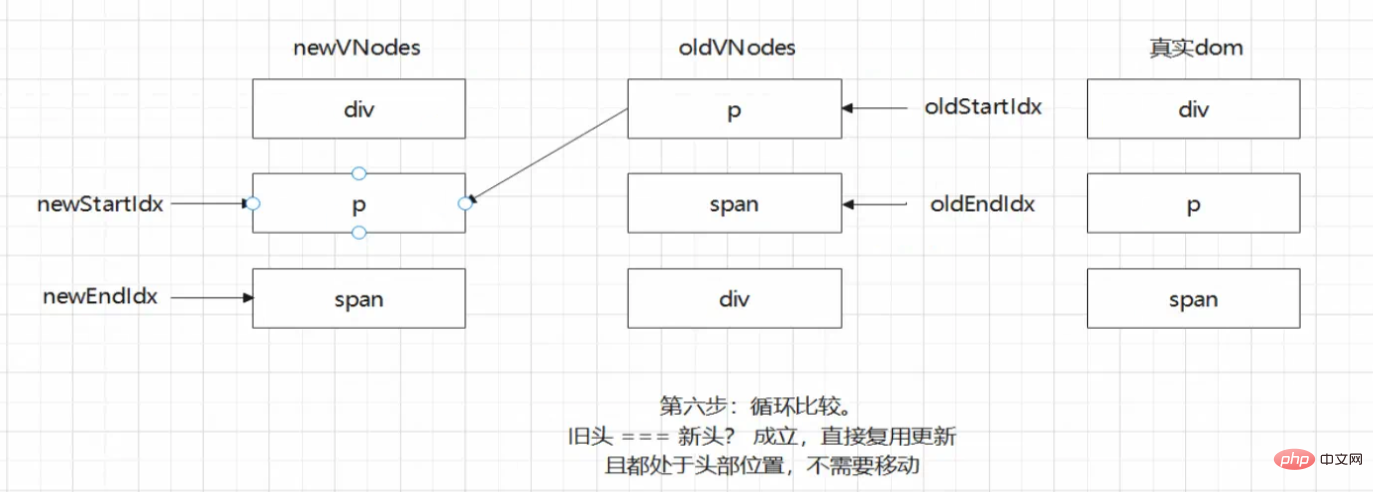
上述的情况是一种非常理想的情况，我们可以根据现有的diff算法完全的处理两组节点，因为每一轮的双端比较都会命中其中一种情况使得其可以完成处理。

但往往会有其他的情况，比如下面这个例子：

const oldChildren = [
    {type: &#39;p&#39;, children: &#39;p&#39;, key: 1},
    {type: &#39;span&#39;, children: &#39;span&#39;, key: 2},
    {type: &#39;div&#39;, children: &#39;div&#39;, key: 3},
    {type: &#39;ul&#39;, children: &#39;ul&#39;, key: 4},
]
const newChildren = [
    {type: &#39;div&#39;, children: &#39;new div&#39;, key: 3},
    {type: &#39;p&#39;, children: &#39;p&#39;, key: 1},
    {type: &#39;ul&#39;, children: &#39;ul&#39;, key: 4},
    {type: &#39;span&#39;, children: &#39;span&#39;, key: 2},
]

Salin selepas log masuk

此时我们会发现，上述的四个步骤都会无法命中任意一步。所以需要额外的步骤进行处理。即是：在四步比较失败后，找到新头节点在旧节点中的位置，并进行移动即可。动图示意如下：

Fahami algoritma Vue Diff dalam satu artikel

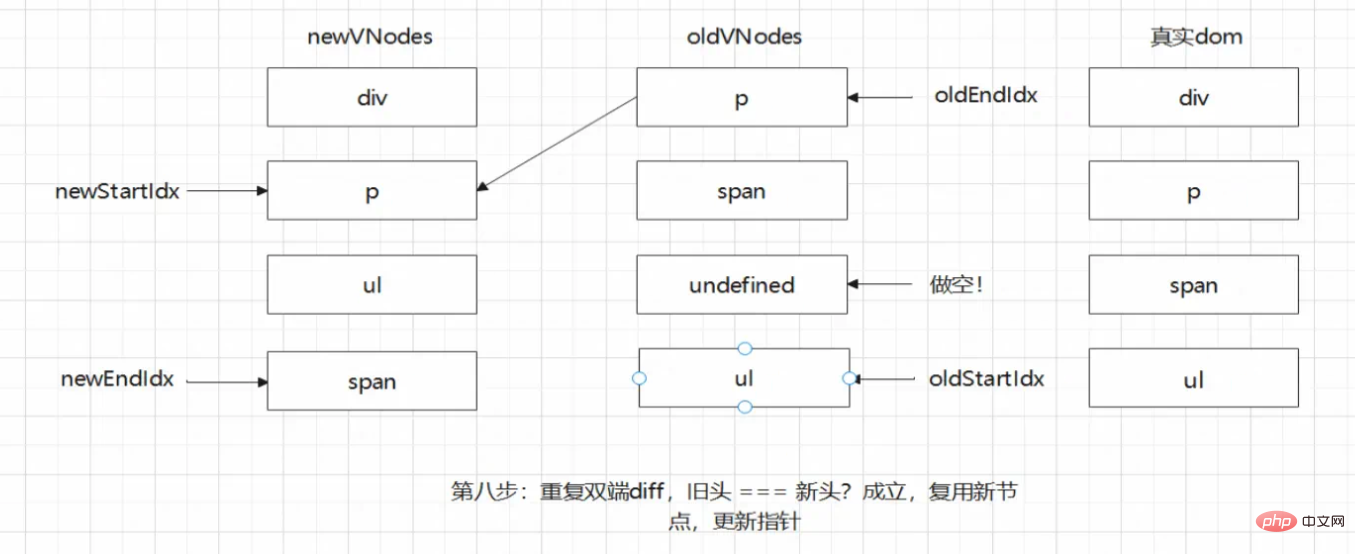
当然还有删除、增加等均不满足上述例子的操作，但操作核心一致，这里便不再赘述。

总结

双端diff算法的优势在于对于一些比较特殊的情况能更快的对节点进行处理，也更贴合实际开发。而双端的含义便在于通过两组子节点的头尾分别进行比较并更新。

快速diff算法

首先，快速diff算法包含了预处理步骤。它借鉴了纯文本diff的思路，这时它为何快的原因之一。

比如：

const text1 = &#39;我是快速diff算法&#39;
const text2 =  &#39;我是双端diff算法&#39;

Salin selepas log masuk

那么就会先从头比较并去除可用元素，其次会重后比较相同元素并复用，那么结果就会如下：

const text1 = &#39;快速&#39;
const text2 = &#39;双端&#39;

Salin selepas log masuk

此时再进行一些其他的比较和处理便会简单很多。

其次，快速diff算法还使用了一种算法来尽可能的复用dom节点，这个便是最长递增子序列算法。为什么要用呢？先举个例子：

// oldVNodes
const vnodes1 = [
    {type:&#39;p&#39;, children: &#39;p1&#39;, key: 1},
    {type:&#39;div&#39;, children: &#39;div&#39;, key: 2},
    {type:&#39;span&#39;, children: &#39;span&#39;, key: 3},
    {type:&#39;input&#39;, children: &#39;input&#39;, key: 4},
    {type:&#39;a&#39;, children: &#39;a&#39;, key: 6}
    {type:&#39;p&#39;, children: &#39;p2&#39;, key: 5},
]
// newVNodes 
const vnodes2 = [
    {type:&#39;p&#39;, children: &#39;p1&#39;, key: 1},
    {type:&#39;span&#39;, children: &#39;span&#39;, key: 3},
    {type:&#39;div&#39;, children: &#39;div&#39;, key: 2},
    {type:&#39;input&#39;, children: &#39;input&#39;, key: 4},
    {type:&#39;p&#39;, children: &#39;p2&#39;, key: 5},
]

Salin selepas log masuk

经过预处理步骤之后得到的节点如下：

// oldVNodes
const vnodes1 = [
    {type:&#39;div&#39;, children: &#39;div&#39;, key: 2},
    {type:&#39;span&#39;, children: &#39;span&#39;, key: 3},
    {type:&#39;input&#39;, children: &#39;input&#39;, key: 4},
    {type:&#39;a&#39;, children: &#39;a&#39;, key: 6},
]
// newVNodes 
const vnodes2 = [
    {type:&#39;span&#39;, children: &#39;span&#39;, key: 3},
    {type:&#39;div&#39;, children: &#39;div&#39;, key: 2},
    {type:&#39;input&#39;, children: &#39;input&#39;, key: 4},
]

Salin selepas log masuk

此时我们需要获得newVNodes节点相对应oldVNodes节点中的下标位置，我们可以采用一个source数组，先循环遍历一次newVNodes，得到他们的key，再循环遍历一次oldVNodes，获取对应的下标关系，如下：

const source = new Array(restArr.length).fill(-1)
// 处理后
source = [1, 2, 0, -1]

Salin selepas log masuk

注意！这里的下标并不是完全正确！因为这是预处理后的下标，并不是刚开始的对应的下标值。此处仅是方便讲解。其次，source数组的长度是剩余的newVNodes的长度，若在处理完之后它的值仍然是-1则说明当前的key对应的节点在旧节点数组中没有，即是新增的节点。

此时我们便可以通过source求得最长的递增子序列的值为 [1, 2] 。对于index为1，2的两个节点来说，他们的相对位置在原oldVNodes中是没有变化的，那么便不需要移动他们，只需要移动其余的元素。这样便能达到最大复用dom的效果。

步骤

以上述例子来说：

首先进行预处理

Fahami algoritma Vue Diff dalam satu artikel

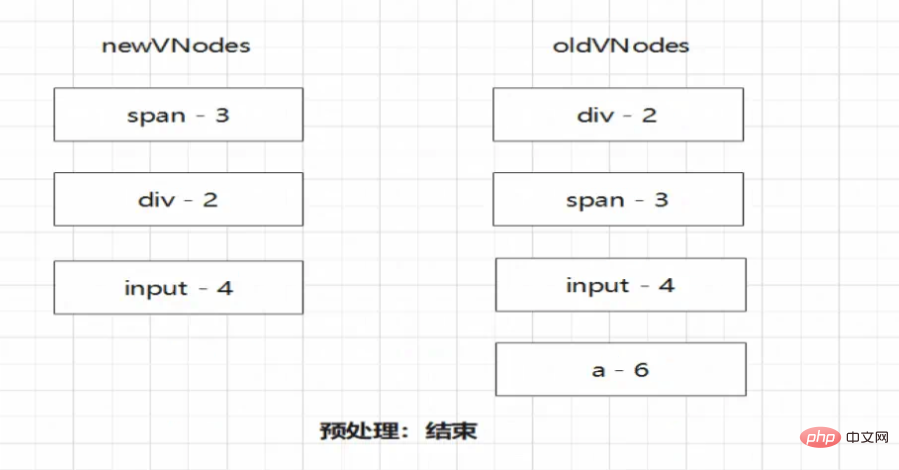
注意！预处理过的节点虽然复用，但仍然需要进行更新。

进行source填充

Fahami algoritma Vue Diff dalam satu artikel

当然这里递增子序列 [1, 2] 和 [0, 1]都是可以的。

进行节点移动

用索引i指向新节点数组中的最后一个元素

用索引s指向最长递增子序列中的最后一个元素

然后循环进行以下步骤比较：

source[i] === -1？等于代表新节点，挂载即可。随后移动i

i === 递增数组[s]? 等于代表当前的节点存在在递增子序列中，是复用的节点，当前的节点无需移动。

上述均不成立代表需要移动节点。

Fahami algoritma Vue Diff dalam satu artikel

节点更新，结束。

总结

核心思路便是进行了类似文本预处理的步骤去除头尾重复的节点。其次便是采用了最长递增子序列来复用相对位置没有发生变化的节点，这些节点是不需要移动的，便能最快的复用和更新。

最后

其实不论是哪一种diff算法，它都需要遵循同样的处理规则：

判断哪些节点需要移动，以及如何移动。

找出那些需要被添加的或者被移除的节点。

【相关推荐：javascript视频教程、vue.js教程】

Atas ialah kandungan terperinci Fahami algoritma Vue Diff dalam satu artikel. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!