Algoritma pengisihan biasa untuk struktur data Java (perkongsian ringkasan)-javaTutorial-php.cn

Artikel ini membawa anda pengetahuan yang berkaitan tentang Java, yang terutamanya memperkenalkan beberapa algoritma pengisihan biasa, termasuk pengisihan sisipan langsung, pengisihan bukit (mengurangkan pengisihan tambahan), pengisihan pemilihan dan pengisihan timbunan, dsb. , mari kita lihat bersama-sama , saya harap ia akan membantu semua orang.

Algoritma pengisihan biasa untuk struktur data Java (perkongsian ringkasan)

1. Perintah pengiktirafan

Di sekolah, jika kita ingin menyertai pertemuan sukan atau latihan ketenteraan, kita akan Berbaris mengikut ketinggian dari pendek ke tinggi Contohnya, kertas kehadiran yang dipegang oleh guru di dalam kelas biasanya disusun mengikut nombor pelajar dari rendah ke tinggi. Contoh lain ialah kedudukan bahasa pengaturcaraan, yang juga disusun.

Terdapat beberapa senario pengisihan dalam kehidupan dapat dilihat bahawa pengisihan masih sangat penting.

Apa yang dipanggil pengisihan, ambil contoh kita di atas, ialah operasi menyusun kenaikan atau pengurangan mengikut saiz kata kunci tertentu atau tertentu Ini adalah pengisihan, yang juga melibatkan Kestabilan pengisihan, sebagai contoh:

Sebagai contoh, terdapat satu set data: B D A C A F. Ia perlu diisih mengikut kod ascll mereka Berikut adalah dua A, kita panggil A yang pertama itu muncul A1, dan A kedua yang muncul A2.

Anggapkan bahawa hasil isihan ialah: A1 A2 B C D F, maka algoritma isihan ini adalah stabil.

Anggapkan bahawa hasil isihan ialah: A2 A1 B C D F, maka algoritma isihan ini tidak stabil.

Ringkasnya, jika terdapat dua elemen yang sama dalam data yang hendak diisih, hubungan antara dua elemen itu tidak akan berubah selepas pengisihan selesai Contohnya, A1 berada di hadapan A2 sebelum ini pengisihan. Selepas mengisih, A1 masih di hadapan A2 Ini adalah algoritma pengisihan yang stabil.

Nota: Algoritma pengisihan yang tidak stabil sememangnya tidak stabil, tetapi algoritma pengisihan yang stabil boleh direka bentuk untuk menjadi tidak stabil.

2. Klasifikasi pengisihan biasa

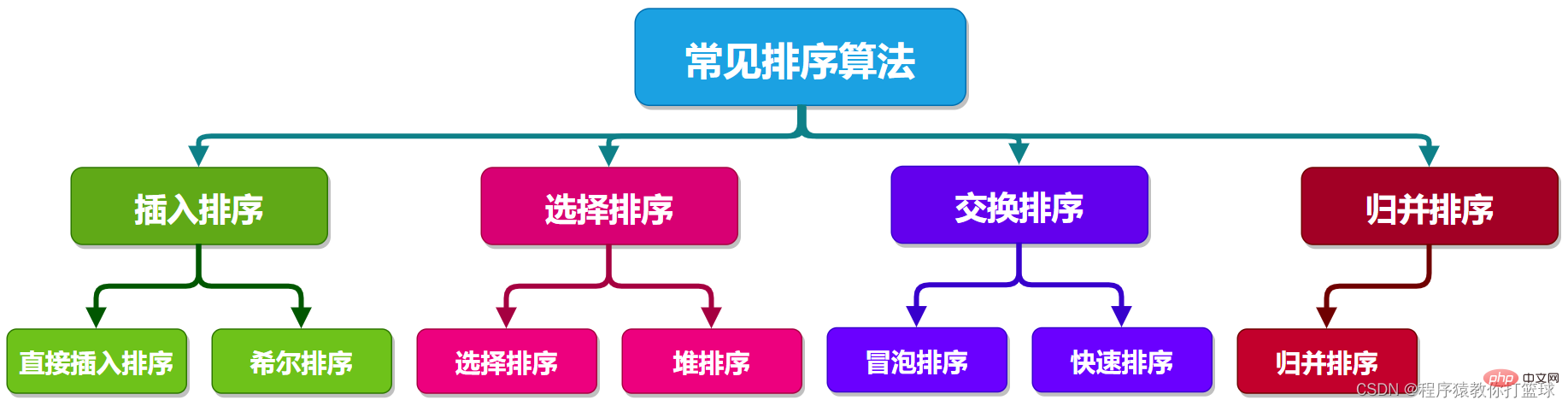
Gambar ini meringkaskan algoritma pengisihan yang akan kita bincangkan kemudian, dan kemudian secara rasmi memasuki kajian bab ini! (Dalam bab algoritma pengisihan, lalai ialah tertib menaik) Nota: Log kerumitan yang disebut kemudian adalah berdasarkan 2, dan yang istimewa akan ditanda.

3. Pengisihan sisipan langsung

Sekarang saya ingin meminta anda semua membayangkan bahawa anda sedang menyentuh kad bermain, dan anda menyentuh kad pertama dan meletakkannya di tangan anda, dan kemudian Lukis satu kad, bandingkan kad ini dengan kad di tangan anda, dan letakkan pada kedudukan yang sesuai. Kemudian lukis satu lagi kad, bandingkan kad ini dengan dua kad di tangan anda, dan letakkan pada kedudukan yang sesuai.

Ini adalah pengisihan sisipan secara ringkas, elemen yang kita ambil setiap kali akan dimasukkan ke dalam urutan yang tersusun, iaitu sebelum setiap kad diambil, kad di tangan diisih hanya perlu membandingkan kad yang baru dilukis dengan kad yang dipesan di tangan kita dan meletakkannya pada kedudukan yang sesuai!

Di sini kami menggunakan gambar statik untuk menunjukkan secara ringkas:

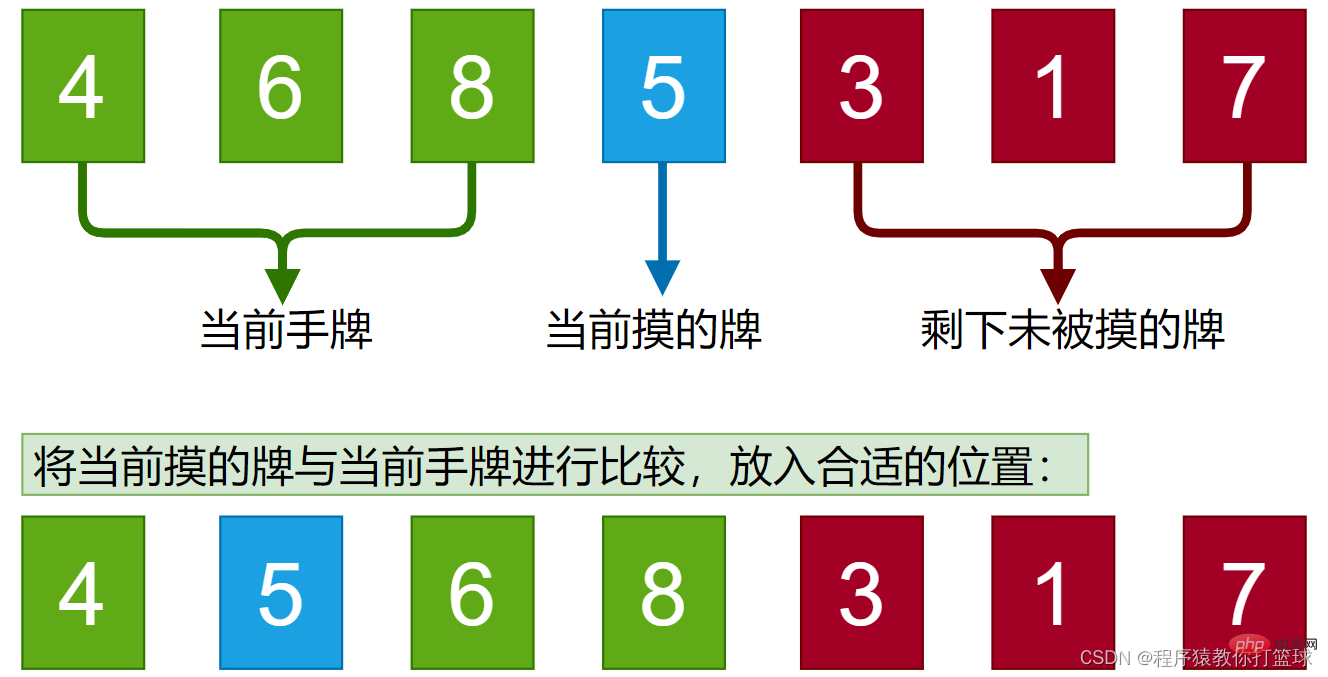
Kami sudah memahami idea umum, seterusnya Kami perlu menggunakan kod untuk melaksanakannya:

public void insertSort(int[] array) {
    // 外循环控制趟数, 第一张牌默认有序, 所以 i 从 1 开始
    for (int i = 1; i < array.length; i++) {
        int tmp = array[i]; //当前摸到的牌
        // 每次从手中牌的最后一张牌开始比较, 一直比到第一张牌
        int j = i - 1;
        for (; j >= 0; j--) {
            //如果当前位置的牌,大于我摸到的牌,就往后挪
            if (array[j] > tmp) {
                array[j + 1] = array[j];
            } else {
                break;
            }
        }
        // 把摸到的牌放到对应位置上
        array[j + 1] = tmp;
    }
}

Salin selepas log masuk

Analisis kerumitan masa: Gelung luar mengambil n - 1 kali jumlahnya dan gelung dalam adalah yang paling teruk setiap kali Dalam kes , adalah perlu untuk membandingkan 1....n kali, kemudian keluarkan sebutan kecil sebelum n, iaitu, (n - 1) * n kali, iaitu, n^2 - n, keluarkan sebutan minimum , dan masa akhir adalah kompleks Darjah ialah O(n^2)

Analisis kerumitan ruang: hanya membuka pembolehubah tmp i, j, pemalar, iaitu kerumitan ruang: O(1)

Kestabilan: Stabil

Semakin dekat data untuk dipesan dalam pengisihan ini, semakin tinggi kecekapan masa.

4. Pengisihan bukit (pengisihan tambahan yang dikurangkan)

Isihan ini ialah pengoptimuman pengisihan sisipan langsung. Anda boleh bayangkan bahawa terdapat baris sebelah menyebelah di hadapan anda. Terdapat 8 plat nombor cinta, tetapi ia tidak teratur pengisihan dilakukan. Kali kedua Selang pertama ialah sekumpulan 2 plat nombor, dan selang sisipan terus dilakukan Selang ketiga ialah sekumpulan 1 plat nombor, dan selang ketiga ialah sekumpulan plat nombor, dan isihan sisipan langsung dilakukan.

Sikit-sikit tak faham ni, tak apa, jom lukis gambar untuk faham apa yang saya cakap di atas semula:

由上图我们可以发现，当间隔 > 1 的时候，都是预排序，也就是让我们的数据更接近有序，但是当间隔为 1 的时候，就是直接插入排序了，前面我们说过，直接插入排序，再数据接近有序的时候时间效率是很快的。由此可见，希尔排序，是直接插入排序的优化版。

如何在代码中实现呢？间隔的值如何取呢？代码中把这个间隔的值称为 gap，这个 gap 的取值方法有很多，有的人提出 gap 为奇数好，有的提出 gap 为偶数好，我们就采取一种比较简单的方法来取 gap 值，首次取数组长度一半的值为 gap，后续 gap /= 2，即可。当 gap 为 1，也就是直接插入排序了。

代码实现如下：

public void shellSort(int[] array) {
    // gap初始值设置成数组长度的一半
    int gap = array.length >> 1;
    // gap 为 1 的时候直接插入排序
    while (gap >= 1) {
        shell(array, gap);
        gap >>= 1; // 更新 gap 值 等价于 -> gap /= 2;
    }
}
private void shell(int[] array, int gap) {
    for (int i = gap; i < array.length; i++) {
        int tmp = array[i];
        int j = i - gap;
        for (; j >= 0; j -= gap) {
            if (array[j] > tmp) {
                array[j + gap] = array[j];
            } else {
                break;
            }
        }
        array[j + gap] = tmp;
    }
}

Salin selepas log masuk

如果实在是不好理解，就结合上边讲的直接插入排序来理解，相信你能理解到的。

时间复杂度分析：希尔排序的时间复杂度不好分析，这里我们就大概记一下，约为 O(n^1.3)，感兴趣的话，可以查阅一下相关书籍。

空间复杂度分析：仍然开辟的是常数个变量，空间复杂度为 O(1)

稳定性：不稳定

5、选择排序

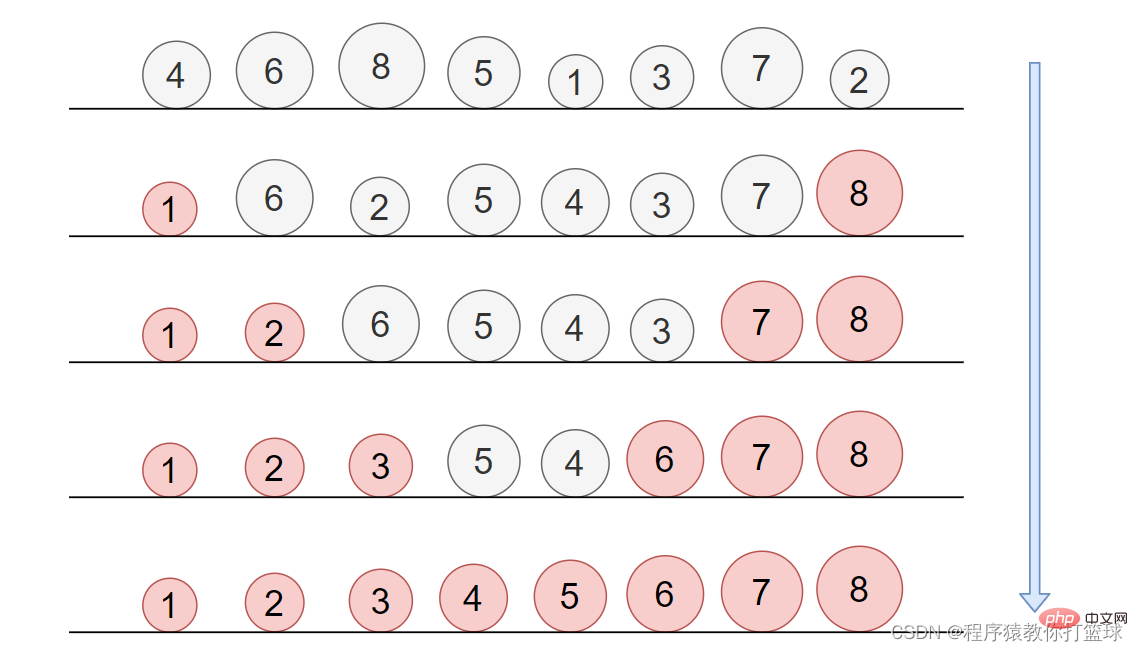
这个排序是个很简单的排序，你想象一下，有个小屁孩，喜欢玩小球，我给他安排了个任务，把这一排小球从小到大排列起来，摆给我看，于是小屁孩就找，每次从一排小球中找出最大的，放到最后，固定不动，那是不是也就是说，每次能确定一个最大的石子的最终位置了。我们来看图：

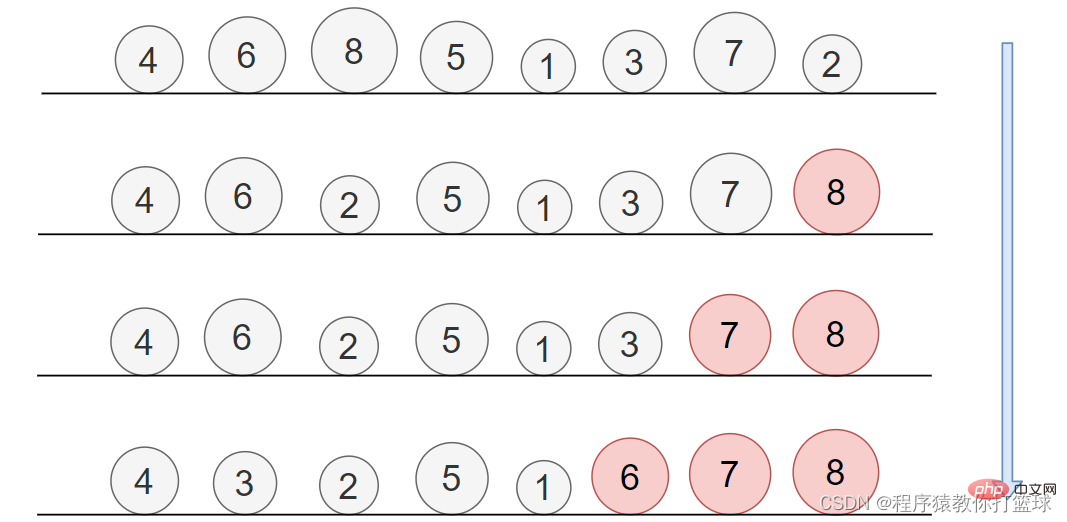
通过图片我们也能看出来，每次找到最大值于最后一个值交换，所以每趟都能把最大的放到最后固定不动，每趟能排序一个元素出来，那这样用代码来实现就很简单了：

public void selectSort(int[] array) {
    int end = array.length - 1;
    // 剩最后一个元素的时候, 不用比较了, 已经有序了
    // 所以 i < array.length - 1
    for (int i = 0; i < array.length - 1; i++) {
        int max = 0;
        int j = 0;
        while (j <= end) {
            if (array[j] > array[max]) {
                max = j;
            }
            j++;
        }
        //找到了最大值的下标, 把最大值与最后一个值交换
        swap(array, max, end--); // end-- 最后一个元素固定了, 不用参与比较
    }
}

Salin selepas log masuk

这个算法有没有可以优化的空间呢？

有！那么既然小屁孩能一次找出最大的球，那能不能让小屁孩一次找出两个球出来呢？分别是这些球中，最大的和最小的，最大的放在最右边，最小的放在最左边，那么我们每次就能确定两个球的最终位置，也就是我们一次能排序两个元素。图解：

代码实现如下：

public void selectSort(int[] array) {
    int left = 0;
    int right = array.length - 1;
    while (left < right) {
        int maxIndex = left;
        int minIndex = left;
        // i = left + 1 -> 每次找最大最小值下标的时候, 可以不用算默认给的最大值和最小值下标
        for (int i = left + 1; i <= right; i++) {
            if (array[i] > array[maxIndex]) {
                maxIndex = i;
            }
            if (array[i] < array[minIndex]) {
                minIndex = i;
            }
        }
        swap(array, minIndex, left);
        // 如果最大值为 left 的位置情况的话, 走到这, 最大值已经被交换到 min 位置上了
        if (maxIndex == left) {
            // 更新最大值的位置
            maxIndex = minIndex;
        }
        swap(array, maxIndex, right);
        left++;
        right--;
    }
}

Salin selepas log masuk

时间复杂度分析：虽然是优化了，但去小项之后，还是 O(n^2)
空间复杂度分析：O(1)
稳定性：不稳定
实际开发中用的不多

6、堆排序

如果你有学习过优先级队列，或者看过博主优先级队列的文章，那么这个排序对于你来说还是很轻松的，当然在堆排序的讲解中，不会过多的去介绍堆的概念，如果对这部分概念还不理解，可以移至博主的上一篇文章进行学习。

堆排序，简单来说，就是把一组数据，看成一个完全二叉树，再把这棵树，建大堆或者建小堆，接着进行排序的一种思路。至于如何建大堆或小堆，和向上调整算法以及向下调整算法，这里也不多介绍了，博主的上篇文章都详细介绍过。

这里我们来分析一下，排升序应该建什么堆？大堆！排降序建小堆！

这里我们来排升序，建大堆，因为大堆堆顶元素一定是堆中最大的，所以我们可以把堆顶元素和最后一个元素进行交换，这样我们就确认了最大值的位置，接着将交换后的堆顶元素进行向下调整，仍然使得该数组满足大堆的特性！图解如下：

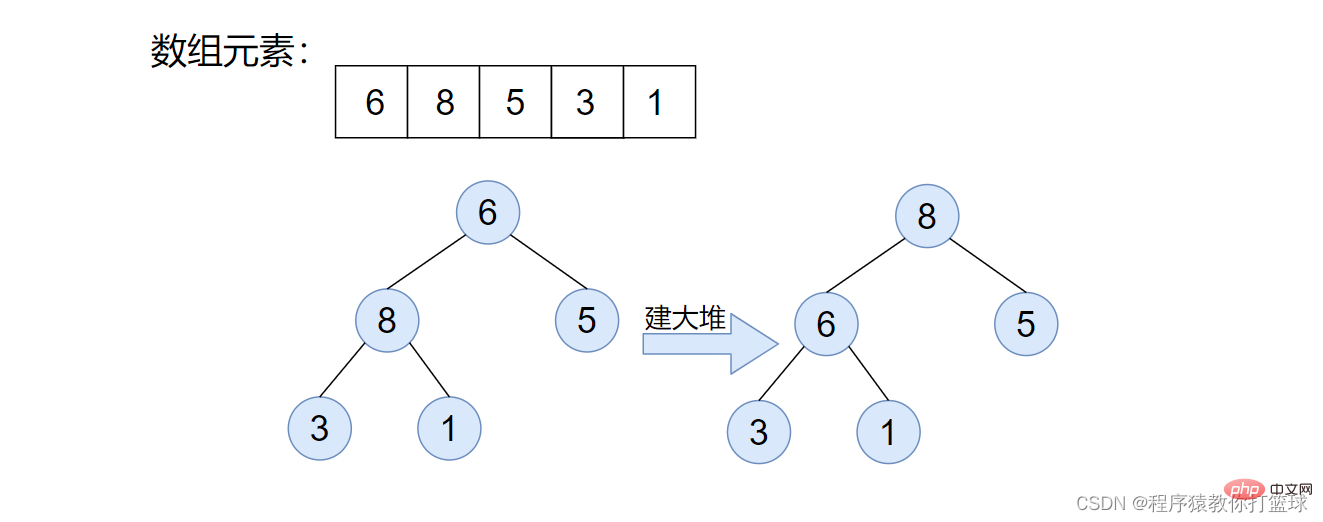
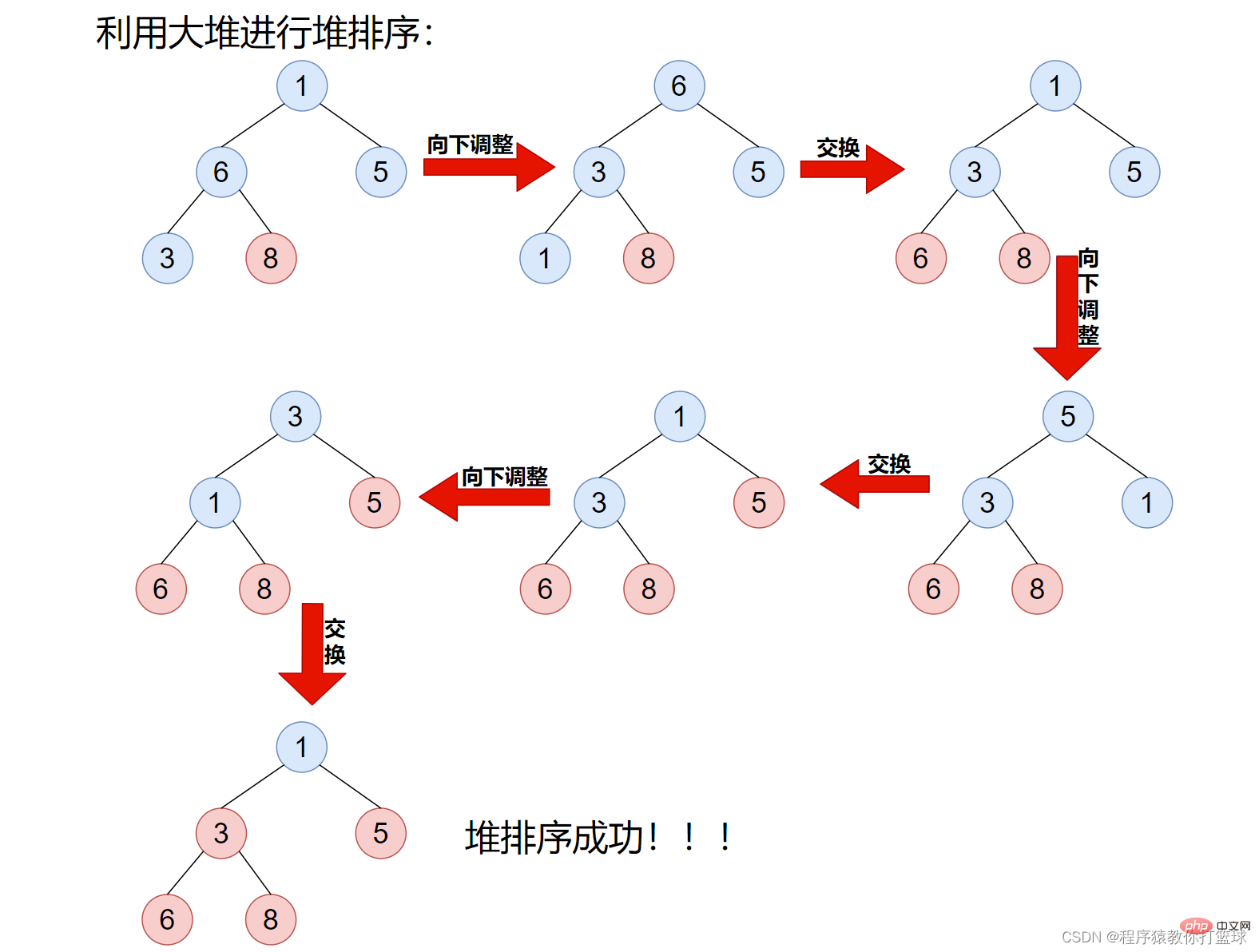
如上图步骤也很简单，先是将数组建成大堆，然后利用大堆来进行堆排序，首先将堆顶元素和最后一个元素交换，由此最大的元素就有序了，接着将该堆进行向下调整，使继续满足大堆性质，依次进行下去即可。

代码实现：

public void heapSort(int[] array) {
    // 建大堆 从最后一个非叶子节点开始向下调整
    // 非叶子节点下标 = (孩子节点下标 - 1) / 2
    for (int parent = (array.length - 1 - 1) / 2; parent >= 0; parent--) {
        shiftDown(array, parent, array.length);
    }
    // 建大堆完成后, 每次堆顶元素与最后一个元素交换, 锁定最大元素的位置
    for (int len = array.length - 1; len > 0; len--) {
        swap(array, 0, len); //根节点与最后一个元素交换
        shiftDown(array, 0, len); //根节点位置向下调整
    }
}
private void shiftDown(int[] array, int parent, int len) {
    int child = parent * 2 + 1;
    while (child < len) {
        if (child + 1 < len && array[child + 1] > array[child]) {
            child++;
        }
        // 判断父节点是否大于较大的孩子节点
        if (array[parent] < array[child]) {
            swap(array, parent, child);
            // 更新下标的位置
            parent = child;
            child = parent * 2 + 1;
        } else {
            return;
        }
    }
}

Salin selepas log masuk

时间复杂度分析：建堆的时间复杂度优先级队列那期有说过为 O(n)，排序调整堆的时候，一共要调整 n-1 次，每次向下调整的时间复杂度是 logn，所以即 logn(n - 1)，即 O(n*logn)，加上面建堆的时间复杂度：O(n) + O(n*logn)，最终时间复杂度也就是：O(n*logn)。

空间复杂度分析：O(1)

稳定性：不稳定

推荐学习：《java视频教程》

Atas ialah kandungan terperinci Algoritma pengisihan biasa untuk struktur data Java (perkongsian ringkasan). Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!