CMU Zhang Kun: Kemajuan terkini dalam teknologi perwakilan sebab

1. Mengapa mengambil berat tentang sebab-sebab

Pertama sekali, mari kita perkenalkan apa itu sebab:

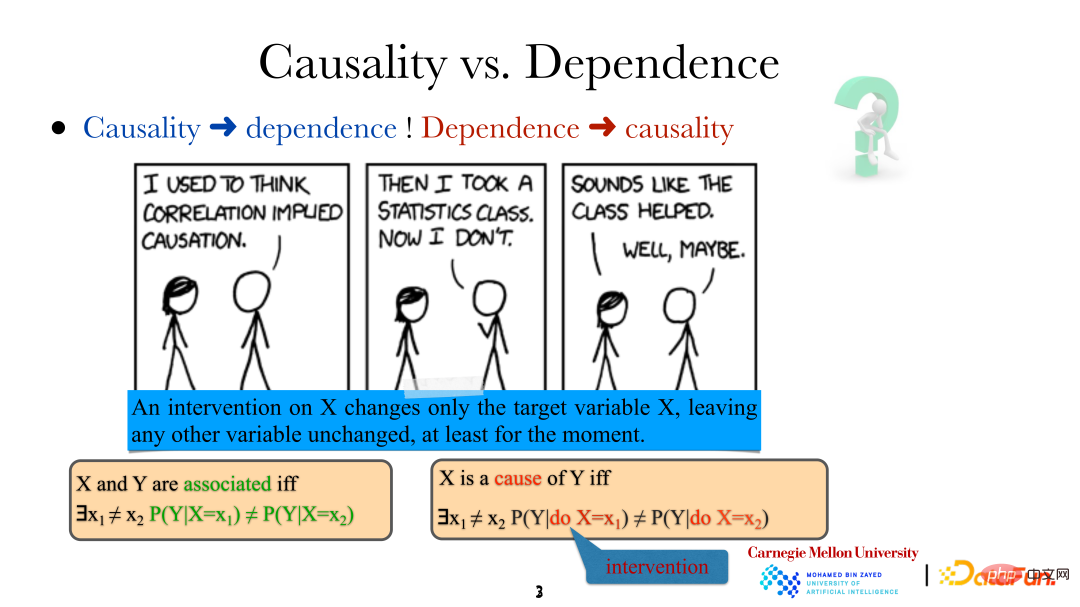
Bila kita katakan Terdapat hubungan antara pembolehubah/peristiwa, yang bermaksud bahawa mereka tidak bebas, jadi mesti ada hubungan antara mereka. Walau bagaimanapun, maksud X menjadi "punca" Y ialah jika kaedah tertentu digunakan untuk menukar X (hujan), Y (tanah menjadi basah) akan berubah dengan sewajarnya, iaitu apabila "campur tangan" campur tangan manusia adalah dilakukan pada Tidak sama. Perlu diingatkan bahawa campur tangan di sini bukan secara rawak, tetapi kawalan langsung yang sangat tepat terhadap pembolehubah sasaran (secara langsung mengubah "hujan" Perubahan ini tidak akan menjejaskan pembolehubah lain secara langsung dalam sistem. Pada masa yang sama, dengan cara ini, iaitu campur tangan manusia secara langsung, kita juga boleh menentukan sama ada satu pembolehubah adalah punca langsung pembolehubah yang lain.

Berikut ialah contoh keperluan untuk menganalisis hubungan sebab akibat:

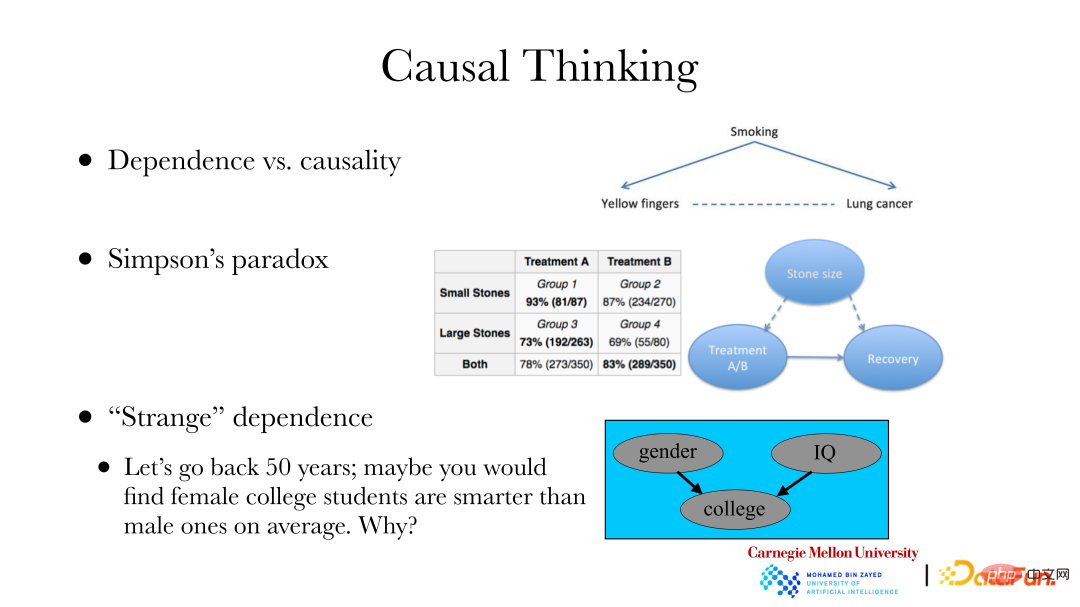
① Kes klasik ialah: penyakit paru-paru dan warna kuku adalah berkaitan antara satu sama lain melalui merokok. Hubungannya ialah kerana rokok tidak mempunyai penapis, merokok secara tetap akan menjadikan kuku anda menjadi kuning, dan merokok juga boleh menyebabkan penyakit paru-paru. Jika anda ingin mengubah kejadian penyakit paru-paru di kawasan tertentu, ia tidak boleh diperbaiki dengan melunturkan kuku anda. Anda perlu mencari punca penyakit paru-paru, bukannya mengubah pergantungan penyakit paru-paru. Untuk mencapai matlamat mengubah kejadian penyakit paru-paru, analisis kausal diperlukan.

② Kes kedua ialah: Simpson’s Paradox. Bahagian kanan gambar di atas adalah set data sebenar Set data menunjukkan dua set data batu karang, satu kumpulan mempunyai batu yang lebih kecil dan satu lagi mempunyai batu yang lebih besar; Terdapat dalam jadual bahawa tidak kira kumpulan batu kecil atau kumpulan batu besar, keputusan yang diperoleh dengan kaedah rawatan A adalah lebih baik, dengan kadar penyembuhan masing-masing 93% dan 73%, dan kadar penyembuhan kaedah rawatan B adalah. 87% dan 69% masing-masing. Walau bagaimanapun, apabila dua kumpulan pesakit batu dengan kaedah rawatan yang sama dicampurkan, kesan keseluruhan pelan rawatan B (83%) adalah lebih baik daripada pelan rawatan A (78%). Katakan anda seorang doktor yang hanya mementingkan kadar kesembuhan, cara memilih pelan rawatan untuk pesakit baru. Sebabnya ialah apabila membuat pengesyoran, kami hanya mengambil berat tentang hubungan sebab akibat antara rawatan dan penawar, dan tidak mengambil berat tentang kebergantungan lain. Walau bagaimanapun, saiz batu adalah faktor biasa dalam kedua-dua kaedah rawatan dan sama ada ia sembuh, yang membawa kepada perubahan kuantitatif dalam pergantungan kaedah rawatan dan penawar. Oleh itu, apabila mengkaji hubungan antara kaedah rawatan dan penawar, kita harus membincangkan hubungan sebab akibat antara yang pertama dan yang terakhir, dan bukannya hubungan pergantungan.

③ Kes ketiga: 50 tahun yang lalu, statistik menunjukkan bahawa wanita di kolej dan universiti secara purata lebih pintar daripada lelaki, tetapi pada hakikatnya tidak sepatutnya terdapat perbezaan yang ketara. Terdapat bias pemilihan, kerana wanita lebih sukar untuk memasuki kolej berbanding lelaki, iaitu apabila sekolah mengambil pelajar, mereka akan dipengaruhi oleh faktor-faktor seperti jantina dan keupayaan ujian. Apabila "keputusan" telah berlaku, akan ada hubungan antara jantina dan keupayaan peperiksaan. Masalah bias pemilihan juga wujud apabila menggunakan data yang dikumpul daripada Internet. Selalunya terdapat hubungan antara sama ada titik data dikumpul dan atribut tertentu Jika anda hanya menganalisis data yang diletakkan di Internet, anda perlu memberi perhatian kepada faktor ini. Apabila ini direalisasikan, data dengan berat sebelah pemilihan juga boleh dianalisis melalui hubungan sebab akibat, dan kemudian sifat keseluruhan kumpulan itu sendiri boleh dipulihkan atau disimpulkan.

Gambar di atas menunjukkan beberapa masalah pembelajaran mesin/pembelajaran mendalam:

① Kita tahu bahawa terdapat hubungan antara ramalan terbaik dan pengedaran data . Dalam pembelajaran pemindahan, sebagai contoh, jika anda ingin memindahkan model dari Afrika ke Amerika dan masih membuat ramalan yang optimum, ini jelas memerlukan pelarasan penyesuaian model berdasarkan pengedaran data yang berbeza. Pada masa ini, adalah penting untuk menganalisis perubahan yang telah berlaku dalam pengedaran data dan bagaimana ia telah berubah. Mengetahui apa yang telah berubah dalam data membolehkan anda melaraskan model dengan sewajarnya. Contoh lain, apabila membina model AI untuk mendiagnosis penyakit, anda tidak akan berpuas hati dengan keputusan diagnosis yang dicadangkan oleh mesin Anda selanjutnya akan ingin mengetahui mengapa mesin membuat kesimpulan ini, seperti mutasi yang menyebabkan penyakit itu. Di samping itu, cara merawat penyakit menimbulkan banyak persoalan "mengapa". Begitu juga, apabila sistem pengesyoran membuat pengesyoran, ia akan ingin mengetahui sebab ia mengesyorkan item/strategi ini, contohnya, syarikat hanya ingin meningkatkan hasil, atau item/strategi itu sesuai untuk pengguna, atau item/strategi adalah bermanfaat untuk masa depan. Soalan "mengapa" ini semuanya adalah soalan sebab dan akibat.

② Dalam bidang pembelajaran mendalam, terdapat konsep serangan lawan. Seperti yang ditunjukkan dalam rajah, jika anda menambah bunyi tertentu pada gambar panda gergasi di sebelah kiri, atau menukar piksel tertentu, dsb., mesin akan menilai gambar itu sebagai jenis haiwan lain dan bukannya panda gergasi, dan tahap keyakinannya adalah masih sangat tinggi. Namun, bagi manusia, dua gambar ini jelas merupakan panda gergasi. Ini kerana ciri peringkat tinggi yang dipelajari oleh mesin daripada imej pada masa ini tidak sepadan dengan ciri peringkat tinggi yang dipelajari oleh manusia. Jika ciri peringkat tinggi yang digunakan oleh mesin tidak sepadan dengan ciri manusia, serangan musuh mungkin berlaku. Apabila input diubah, pertimbangan manusia atau mesin akan berubah, dan akan ada masalah dengan keputusan penghakiman akhir. Hanya dengan membenarkan mesin mempelajari ciri peringkat tinggi yang konsisten dengan manusia, iaitu mesin boleh belajar dan menggunakan ciri dengan cara yang sama seperti manusia, kita boleh mengelakkan serangan musuh.

Mengapa kita memerlukan perwakilan kausal?

① Manfaatkan tugasan hiliran: Contohnya, ia boleh membantu pengelasan hiliran dan tugasan lain untuk melakukan yang lebih baik.

② Boleh menerangkan soalan "mengapa".

③ Pulihkan ciri penyebab sebenar di sebalik data: Metafizik Kant dalam falsafah percaya bahawa dunia yang dialami oleh manusia adalah dunia empirikal. Walaupun ia berdasarkan dunia-dalam-sendiri di belakangnya, kita tidak dapat melihat secara langsung ontologi dunia Sesetengah sifat, seperti masa, ruang, susunan sebab akibat, dan lain-lain, telah ditambahkan secara automatik ke dunia pengalaman oleh sistem deria. Oleh itu, jika anda mahu mesin mempelajari ciri-ciri yang konsisten dengan manusia, anda memerlukan mesin itu mempunyai keupayaan untuk mempelajari ciri-ciri seperti susunan/hubungan sebab akibat, masa dan ruang.

2. Pembelajaran perwakilan sebab: situasi bebas dan teragih sama

1. Pertama, dua soalan perlu dijawab: Pertama, apakah sifat dalam data yang berkaitan dengan kausaliti, dan apakah petunjuk ("jejak kaki") yang terdapat dalam data. Yang kedua ialah sama ada hubungan sebab-akibat boleh dipulihkan di bawah syarat-syarat mendapatkan data, iaitu isu kebolehcaman sistem sebab-akibat.

Sifat yang paling penting bagi sistem kausal ialah "modulariti": walaupun pembolehubah dalam sistem mempunyai hubungan tertentu, sistem boleh dibahagikan kepada hubungan sebab akibat Pelbagai subsistem (satu punca menghasilkan satu pembolehubah bersandar). Contohnya, "Hujan", "Tanah basah", dan "Tanah licin" adalah saling bergantung, dan ia boleh dibahagikan kepada tiga subsistem melalui hubungan sebab-akibat: "Sesetengah sebab menyebabkan hujan", "Hujan ke menyebabkan tanah menjadi basah" , "Tanah basah menyebabkan tanah menjadi licin." Walaupun terdapat kebergantungan antara pembolehubah, ketiga-tiga proses ini (proses, subsistem) tidak disambungkan, tiada perkongsian parameter, dan perubahan dalam satu sistem tidak akan menyebabkan perubahan dalam sistem yang lain. Sebagai contoh, dengan menyembur bahan tertentu untuk mengubah kesan "tanah basah menyebabkan tanah licin", ini tidak akan menjejaskan sama ada hujan atau tidak, dan ia tidak akan mengubah kesan hujan pada tanah menjadi basah. Sifat ini dipanggil "modularity", yang bermaksud bahawa sistem dibahagikan kepada sub-modul yang berbeza dari perspektif kausal, dan tidak ada hubungan antara sub-modul.

Bermula dari modulariti, kita boleh mendapatkan tiga sifat sistem kausal:

① Kebebasan bersyarat antara pembolehubah.

② Keadaan bunyi bebas.

③ Perubahan minimum (dan bebas).

Mengenai kebolehcaman sistem sebab, secara amnya, pembelajaran mesin itu sendiri tidak begitu memberi perhatian kepada isu kebolehcaman Sebagai contoh, model ramalan perlu menilai sama ada hasil ramalan adalah tepat atau optimum, tetapi ada bukan "kebenaran" untuk diadili. Namun begitu, pembelajaran analisis sebab musabab/causal representation adalah untuk memulihkan "kebenaran" data iaitu lebih memberi perhatian sama ada sifat sebab musabab di sebalik data dapat dikenalpasti.

Dua konsep asas diperkenalkan di bawah:

① Penemuan penyebab: meneroka struktur/model penyebab yang mendasari melalui data.

② Pembelajaran perwakilan sebab: Cari pembolehubah tersembunyi peringkat tinggi asas dan hubungan antara pembolehubah daripada data yang diperhatikan secara langsung.

2. Pembahagian pembelajaran perwakilan sebab

Kaedah pembelajaran perwakilan sebab secara amnya dibahagikan daripada tiga perspektif berikut:

① Sifat data: sama ada ia bebas dan teragih sama ( "data i.i.d." ). Data tidak bebas dan teragih sama termasuk data tidak bebas tetapi teragih sama, seperti data teragih sama dengan pergantungan masa (seperti data siri masa), atau data bebas tetapi teragih berbeza, seperti perubahan pengedaran data (atau dua kombinasi ini daripada mereka).

② Kekangan parameter ("kekangan parameter"): sama ada terdapat sifat tambahan lain pada pengaruh kausalitas, seperti model parametrik.

③ Faktor pengacau yang berpotensi ("pengacau terpendam"): Sama ada membenarkan kewujudan faktor biasa yang tidak diperhatikan atau faktor pengacau dalam sistem.

Rajah berikut menunjukkan secara terperinci keputusan khusus yang boleh diperolehi di bawah tetapan berbeza:

Sebagai contoh, dalam kes pengagihan bebas dan serupa, jika tiada Kekangan model parameter, tidak kira sama ada terdapat potensi faktor pengacau, secara amnya boleh memperoleh kelas kesetaraan ("kelas kesetaraan").

3. Pembelajaran perwakilan kausal bebas dan teragih sama

Rajah di atas menunjukkan contoh tiada kekangan model parameter dalam kes taburan bebas dan serupa. Data menunjukkan sejumlah 8 pembolehubah yang diukur untuk 250 tengkorak, termasuk jantina, lokasi, cuaca serta saiz dan bentuk tengkorak. Ahli arkeologi ingin mengetahui apa yang menyebabkan penampilan orang yang berbeza di kawasan yang berbeza Jika kita mengetahui hubungan sebab akibat ini, kita mungkin dapat meramalkan penampilan orang melalui perubahan persekitaran dan faktor lain. Jelas sekali, campur tangan manusia tidak boleh dilakukan dalam keadaan sedemikian Walaupun campur tangan ditambah, ia akan mengambil masa yang lama untuk memerhatikan hasilnya, jadi hubungan sebab akibat hanya boleh didapati daripada data pemerhatian yang sedia ada.

Seperti yang ditunjukkan dalam rajah di atas, hubungan antara pembolehubah adalah sangat kompleks, ia mungkin linear atau tidak linear, dan dimensi pembolehubah juga mungkin tidak konsisten. Jika jantina ialah 1 dimensi, ciri tengkorak mungkin 255 dimensi. Pada masa ini, sifat kebebasan bersyarat boleh digunakan untuk membina hubungan sebab akibat.

Kaedah termasuk dua berikut:

① Algoritma PC (Peter-Clark): Algoritma menganggap bahawa tiada faktor sepunya diperhatikan dalam sistem.

② Algoritma FCI: digunakan apabila terdapat pembolehubah tersembunyi.

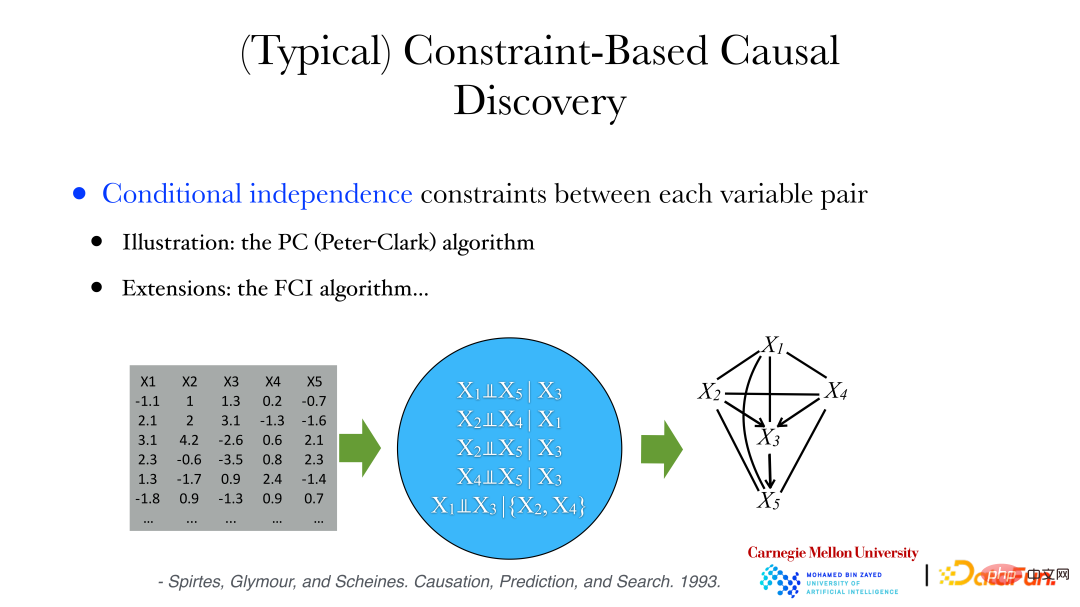
Yang berikut akan menggunakan algoritma PC untuk menganalisis data arkeologi: satu siri sifat tidak bersyarat boleh diperoleh daripada data, seperti pembolehubah X1 dan X5 tidak bersyarat apabila X3 diberikan, dsb. Pada masa yang sama, kita boleh membuktikan bahawa jika dua pembolehubah bebas bersyarat, maka tidak ada kelebihan di antara mereka. Kemudian, kita boleh bermula dari graf lengkap Jika pembolehubah bebas bersyarat, kemudian keluarkan tepi yang disambungkan untuk mendapatkan graf tidak berarah Kemudian nilaikan arah tepi dalam graf untuk mencari graf asiklik terarah Graf) atau koleksi graf akiklik terarah untuk memenuhi kekangan kebebasan bersyarat antara pembolehubah dalam data.

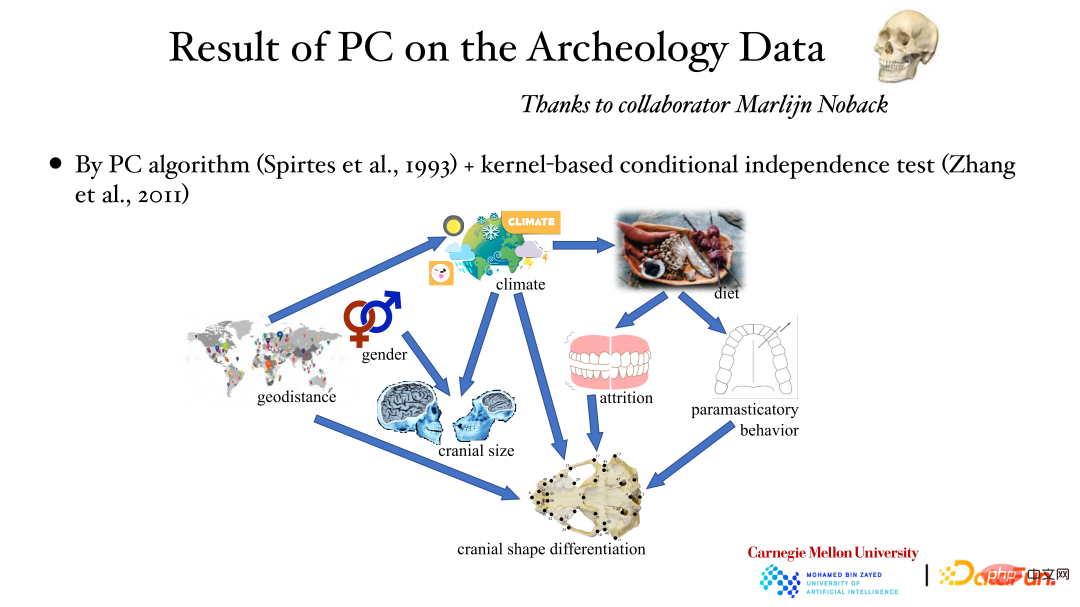
Rajah di atas menunjukkan hasil analisis data arkeologi menggunakan algoritma PC dan kaedah ujian bebas bersyarat kernel: lokasi geografi mempengaruhi cuaca, cuaca mempengaruhi saiz tengkorak, dan jantina juga Boleh menjejaskan saiz tengkorak dll. Hubungan sebab akibat di sebaliknya diperoleh melalui analisis data.

Antara dua masalah yang baru disebut, satu ialah mencari arah setiap tepi pembolehubah DAG, yang memerlukan andaian tambahan. Jika anda membuat beberapa andaian tentang cara sebab mempengaruhi kesan, anda akan mendapati sebab dan akibat adalah tidak simetri, jadi anda boleh mengetahui arah sebab dan akibat. Latar belakang data dalam rajah di bawah masih merupakan data yang bebas dan diedarkan secara serupa, dan sekatan parameter tambahan telah ditambah, dan faktor yang mengelirukan masih tidak dibenarkan dalam sistem. Pada masa ini, tiga jenis model berikut boleh digunakan untuk mengkaji arah sebab musabab:

① Model bukan Gaussian linear

② Model penyebab bukan linear pasca (PNL, Post -nonlinear; model kausal);

③ Model hingar tambahan (ANM, Model hingar tambahan).

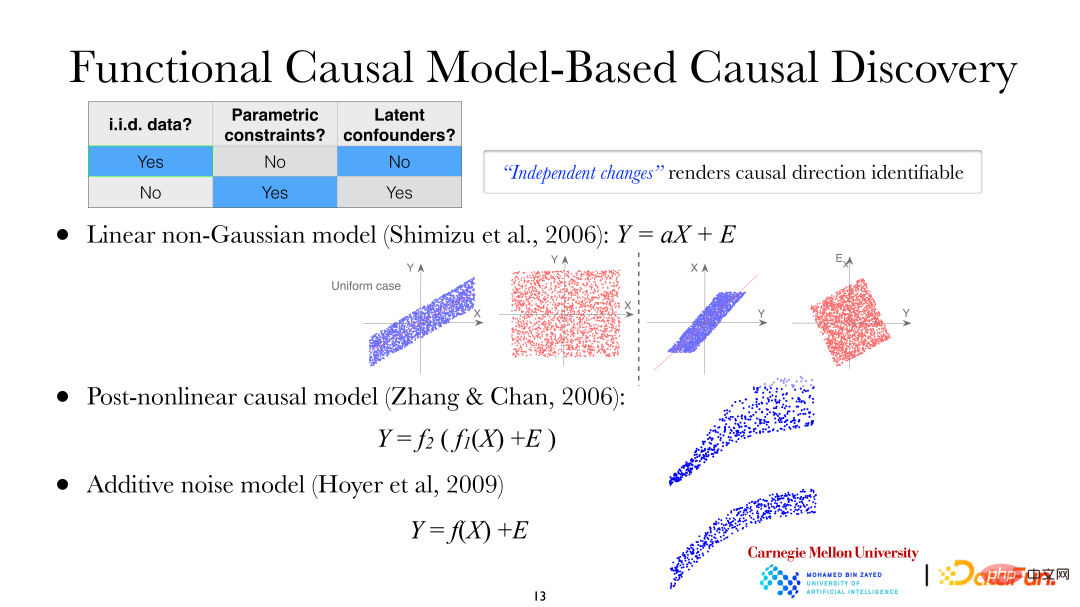
Dalam model linear bukan Gaussian, diandaikan bahawa X membawa kepada Y, iaitu X ialah pembolehubah bersandar dan Y ialah pembolehubah kesan. Ia boleh dilihat daripada rajah bahawa apabila menggunakan X untuk menerangkan Y untuk regresi linear, baki dan X adalah bebas tetapi sebaliknya, apabila menggunakan Y untuk menjelaskan Jelas sekali mereka tidak bebas (dalam kes Gaussian linear, tidak berkorelasi antara pembolehubah bermakna; kemerdekaan. Tetapi pada masa ini model itu adalah linear bukan Gaussian, iaitu, tidak berkorelasi tidak bermakna mereka bebas). Ia boleh didapati bahawa terdapat asimetri antara pembolehubah bersandar dan pembolehubah kesan. Perkara yang sama berlaku untuk model kausal selepas bukan linear dan model hingar tambahan.

Rajah di atas menunjukkan model kausal selepas tak linear: fungsi tak linear kedua (f2) di luar biasanya digunakan untuk menerangkan ketaklinearan yang diperkenalkan dalam proses pengukuran dalam sistem. Perubahan linear, selalunya terdapat perubahan bukan linear semasa memerhati/mengukur data. Sebagai contoh, dalam bidang biologi, akan terdapat perubahan bukan linear tambahan apabila menggunakan instrumen untuk mengukur data ekspresi gen. Model linear, model hingar aditif tak linear dan model hingar darab adalah semua kes khas model PNL.

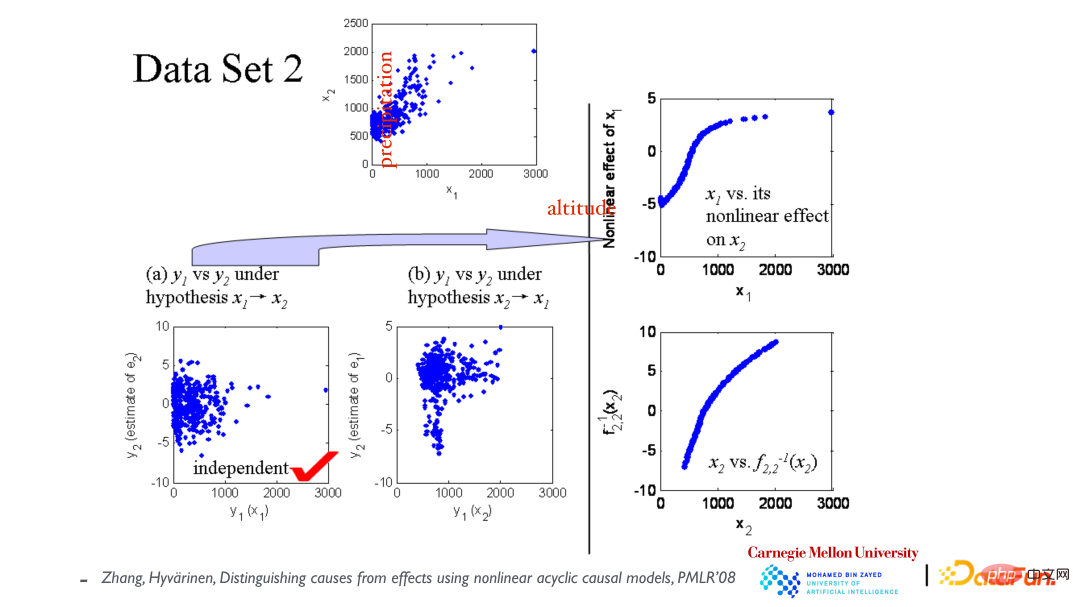
Plot serakan teratas menunjukkan hubungan antara pembolehubah x1 (ketinggian) dan x2 (curahan hujan tahunan). Mula-mula andaikan bahawa x1 menyebabkan x2, dan kemudian bina model untuk memuatkan data Seperti yang ditunjukkan di sudut kiri bawah, baki dan x1 adalah bebas kemudian andaikan bahawa x2 menyebabkan x1, dan sesuai dengan model itu dan x2 tidak Bebas (lihat gambar tengah). Daripada ini, disimpulkan bahawa arah sebab akibat disebabkan oleh x1 yang membawa kepada x2.

Asimetri pembolehubah sebab memang boleh didapati daripada contoh sebelumnya, tetapi adakah keputusan ini boleh dijamin secara teori? Dan ia adalah satu-satunya keputusan yang betul Arah yang bertentangan (kesan kepada sebab) tidak dapat menjelaskan data? Buktinya adalah seperti yang ditunjukkan dalam jadual di atas, dalam lima kes, data boleh dijelaskan dalam kedua-dua arah (sebab akibat, kesan kepada sebab ini adalah kes yang sangat istimewa. Yang pertama ialah model Gaussian linear, di mana hubungannya adalah linear dan taburan adalah Gaussian, di mana asimetri kausal hilang. Empat lagi adalah model istimewa.

Walaupun data dianalisis menggunakan model pasca-bukan linear, sebab dan akibat boleh dibezakan dalam arah yang betul, tetapi tidak dalam arah yang bertentangan arah. Memandangkan model linear dan model hingar tambahan tak linear adalah kedua-dua kes khas model selepas bukan linear, kedua-dua model juga boleh digunakan dalam kes ini dan boleh mencari arah sebab akibat.

Memandangkan dua pembolehubah, arah sebab akibatnya boleh didapati melalui kaedah di atas. Tetapi dalam lebih banyak kes, masalah berikut perlu diselesaikan: Sebagai contoh, dalam bidang psikologi, jawapan kepada beberapa soalan (xi) dikumpul melalui soal selidik Terdapat pergantungan antara jawapan ini, dan ia tidak dianggap ada hubungan antara jawapan ini.

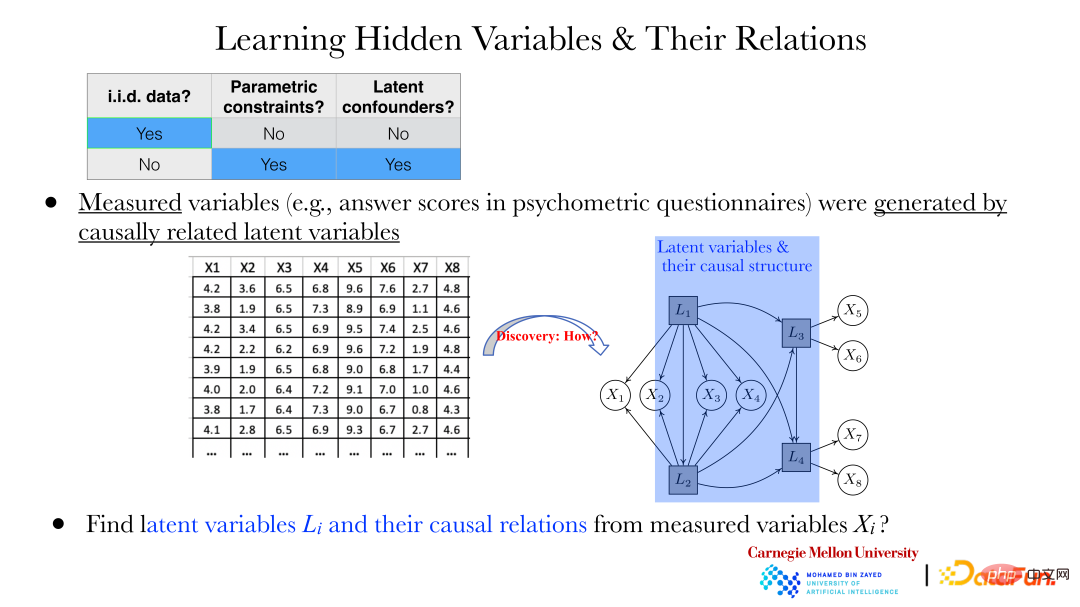
Tetapi seperti yang ditunjukkan dalam rajah di atas, xi ini dijana oleh pembolehubah tersembunyi Li di belakangnya. Cara untuk mendedahkan pembolehubah tersembunyi Li dan hubungan antara pembolehubah tersembunyi melalui xi yang diperhatikan adalah amat penting.

Dalam beberapa tahun kebelakangan ini, terdapat beberapa kaedah yang boleh membantu kami mencari pembolehubah bersandar ini dan hubungannya. Rajah di atas menunjukkan contoh aplikasi kaedah Generalized Independent Noise (GIN), yang boleh menyelesaikan satu siri masalah. Kandungan data adalah kelesuan profesional guru, yang mengandungi 28 pembolehubah. Gambar di sebelah kanan menunjukkan kemungkinan pembolehubah tersembunyi yang dicadangkan oleh pakar mungkin membawa kepada keadaan kelesuan ini (pembolehubah diperhatikan) dan hubungan antara pembolehubah tersembunyi. Keputusan yang diperoleh dengan menganalisis data yang diperhatikan melalui kaedah GIN adalah konsisten dengan keputusan yang diberikan oleh pakar. Pakar menjalankan analisis melalui pengetahuan latar belakang kualitatif, dan kaedah analisis kuantitatif analisis data menyediakan pengesahan dan sokongan untuk keputusan pakar.

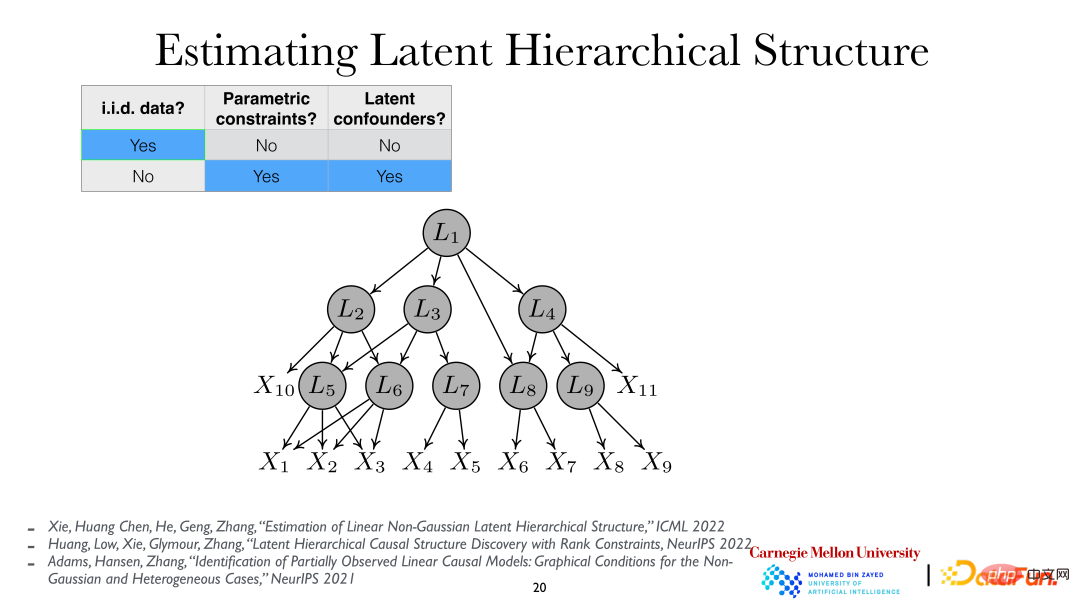
Untuk analisis yang lebih mendalam, boleh diandaikan bahawa pembolehubah terpendam adalah hierarki, iaitu struktur hierarki pembolehubah terpendam (Struktur Hierarki Latent). Dengan menganalisis pembolehubah yang diperhatikan xi, pembolehubah tersembunyi Li dan hubungannya di belakangnya boleh didedahkan.

3. Pembelajaran perwakilan sebab dari siri masa

Memahami kaedah perwakilan sebab dalam kes taburan bebas dan identik, seterusnya kami akan memperkenalkan cara mempelajari perwakilan sebab dalam keadaan tak linear dan bebas dan taburan yang sama. Bagaimana untuk mencari pembolehubah tersembunyi dan hubungan sebab di belakangnya. Secara umumnya, dalam kes taburan bebas dan sama, keadaan yang agak kuat (termasuk andaian model parametrik, model linear, graf jarang, dll.) diperlukan untuk mencari hubungan sebab akibat. Dalam kes lain, penyebab boleh didapati dengan lebih mudah.

Berikut akan memperkenalkan cara mencari perwakilan sebab dari siri masa, iaitu cara melakukan analisis sebab apabila data tidak bebas tetapi diedarkan secara serupa:

Sekiranya kausalitas berlaku dalam siri masa yang diperhatikan, ini adalah masalah klasik mencari kausalitas daripada data siri masa, iaitu kausalitas Granger. Kausalitas Granger adalah konsisten dengan kausalitas yang disebutkan sebelum ini berdasarkan kebebasan bersyarat, tetapi dengan penambahan kekangan masa (jika ia tidak boleh berlaku lebih awal daripada punca), dan tambahan pula, hubungan sebab akibat serta-merta boleh diperkenalkan.

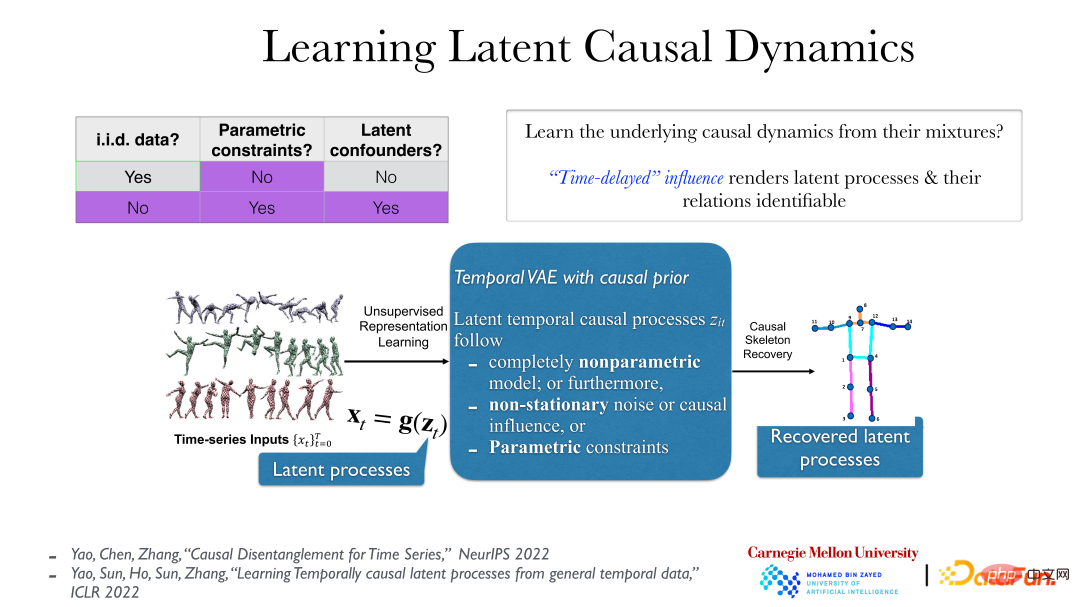
Gambar di atas menunjukkan kaedah yang lebih praktikal. Dalam data video, proses terpendam yang benar-benar bermakna di sebalik data ialah data yang kami amati, sebagai pantulan mereka, dijana oleh transformasinya oleh fungsi tak linear licin boleh balik. Proses sebab akibat yang tersirat secara amnya mempunyai hubungan sebab akibat dalam masa, seperti "tolak dan kemudian jatuh". Di bawah keadaan ini, walaupun di bawah andaian yang sangat lemah (walaupun jika proses pendam asas adalah bukan parametrik dan fungsi g (dari proses pendam kepada siri masa yang diperhatikan) juga bukan parametrik), proses pendam asas boleh difahami sepenuhnya Semua terbongkar.

Ini kerana selepas kembali kepada proses tersirat sebenar, tiada sebab dan pergantungan serta-merta, dan hubungan antara objek akan menjadi lebih jelas. Walau bagaimanapun, jika anda menggunakan kaedah analisis yang salah untuk melihat data pemerhatian, seperti memerhati secara langsung piksel data video, anda akan mendapati bahawa terdapat pergantungan serta-merta antara mereka.

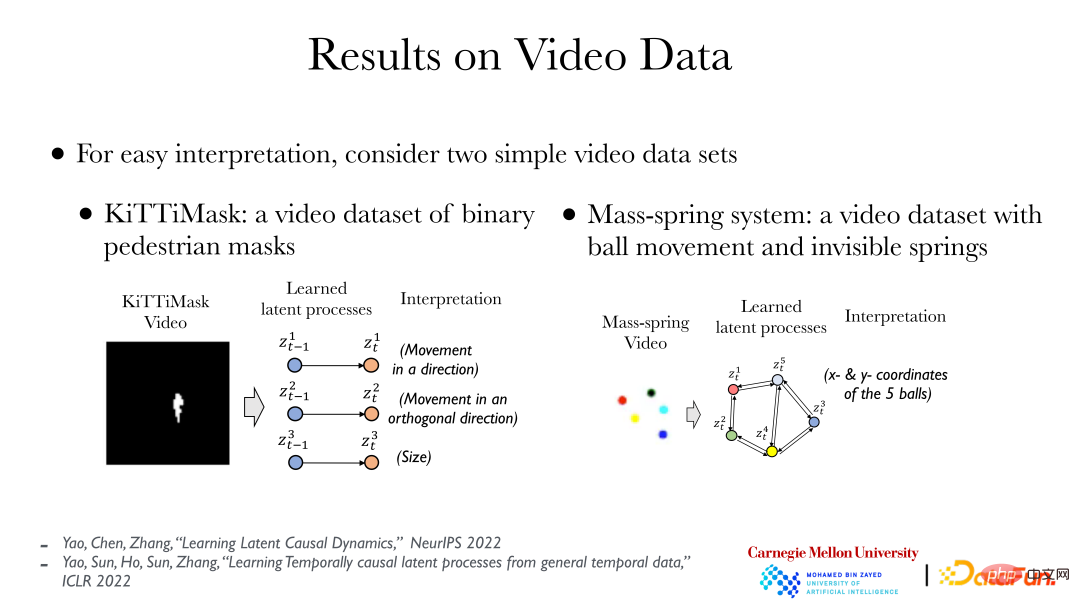
Angka di atas menunjukkan dua kes mudah: sebelah kiri menunjukkan data video KiTTiMask. Menganalisis data video, kami mendapat tiga proses tersembunyi: bergerak dalam satu arah dan menukar saiz topeng. Bahagian kanan menunjukkan 5 bola kecil dengan warna yang berbeza Beberapa bola disambungkan oleh spring (tidak kelihatan), 10 pembolehubah tersembunyi (koordinat x, y bagi 5 bola kecil) boleh diperolehi, dan kemudian sebab dan akibat di antara mereka. boleh didapati hubungan (terdapat mata air antara beberapa bola). Berdasarkan data video, kami boleh terus menggunakan kaedah tanpa pengawasan sepenuhnya dan memperkenalkan prinsip sebab dan akibat untuk mencari hubungan antara objek di belakangnya.

4. Pembelajaran perwakilan sebab di bawah pelbagai pengagihan

Akhir sekali, mari kita perkenalkan analisis sebab apabila pengagihan data berubah:

Bila Bila merekodkan pembolehubah/proses dari semasa ke semasa, selalunya didapati bahawa pengagihan data berubah mengikut masa disebabkan oleh perubahan dalam nilai pembolehubah yang tidak diperhatikan/diukur, seterusnya mengubah pengagihan data pembolehubah yang diperhatikan sebagai tindak balas. Begitu juga, jika anda mengukur data dalam keadaan yang berbeza, anda akan mendapati bahawa pengedaran data yang diukur di bawah keadaan/lokasi yang berbeza mungkin juga berbeza.

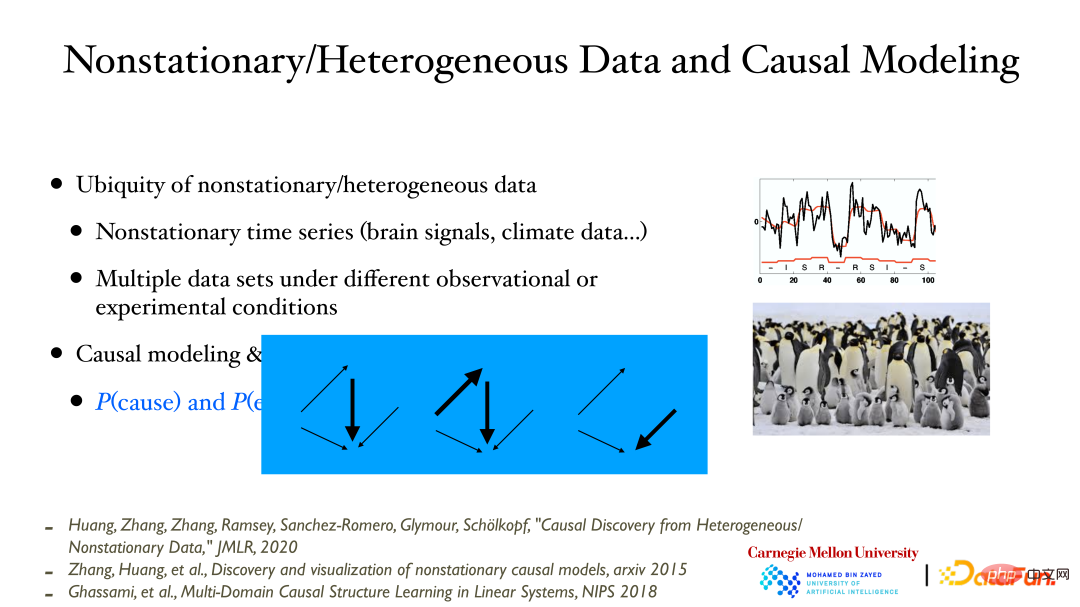
Perkara yang perlu ditekankan di sini ialah terdapat hubungan yang sangat rapat antara pemodelan sebab dan perubahan dalam pengedaran data. Apabila model kausal diberikan, berdasarkan sifat modular, sub-modul ini boleh berubah secara bebas Jika perubahan ini boleh diperhatikan daripada data, ketepatan model kausal boleh disahkan. Perubahan model kausal yang disebutkan di sini bermakna pengaruh kausal boleh menjadi lebih kuat/lemah malah hilang.

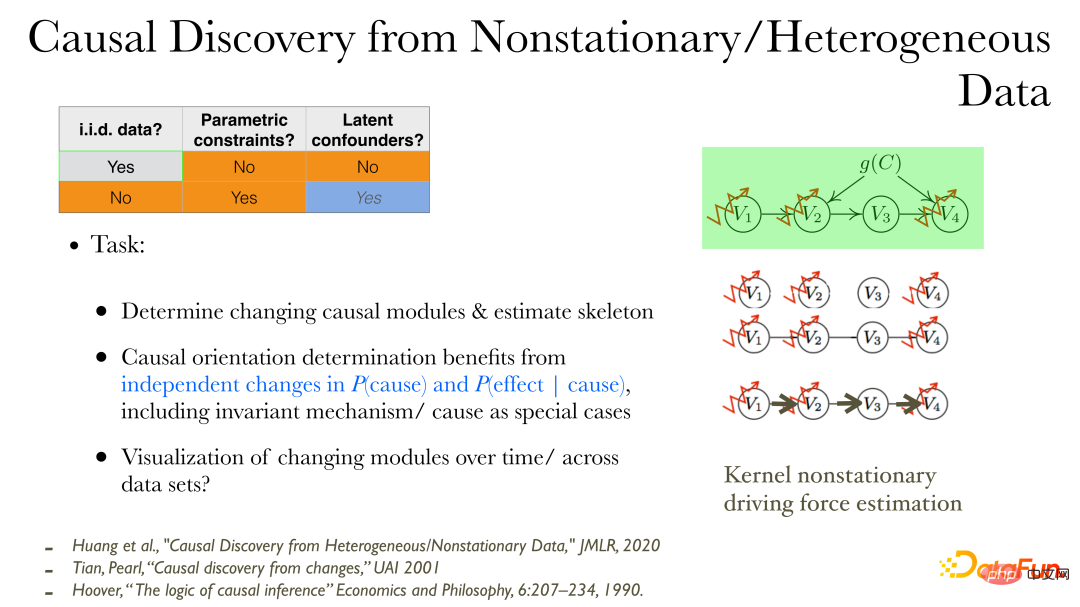
Hubungan sebab boleh diterokai secara langsung dalam data tidak pegun/data heterogen Selepas pembolehubah yang diperhatikan diberikan:

① Pertama, anda boleh memerhati pembolehubah yang mana. ' proses pengeluaran sebab akan berubah; : perubahan dalam sebab dan perubahan dalam kesan mengikut sebab adalah bebas dan tidak berkaitan. Kerana perubahan antara modul berbeza adalah bebas;

④ Gunakan kaedah visualisasi dimensi rendah untuk menerangkan proses perubahan sebab.

Angka berikut menunjukkan beberapa keputusan menganalisis data pulangan harian stok (data segera, tiada lag masa) di Bursa Saham New York:

Pengaruh daripada asimetri antara mereka boleh didapati melalui tidak pegun. Sektor yang berbeza selalunya berada dalam kategori yang sama (kluster) dan berkait rapat. Imej di penjuru kanan sebelah bawah menunjukkan proses penyebab perubahan saham dari semasa ke semasa, dengan dua paksi menegak masing-masing mewakili krisis kewangan 2007 dan 2008.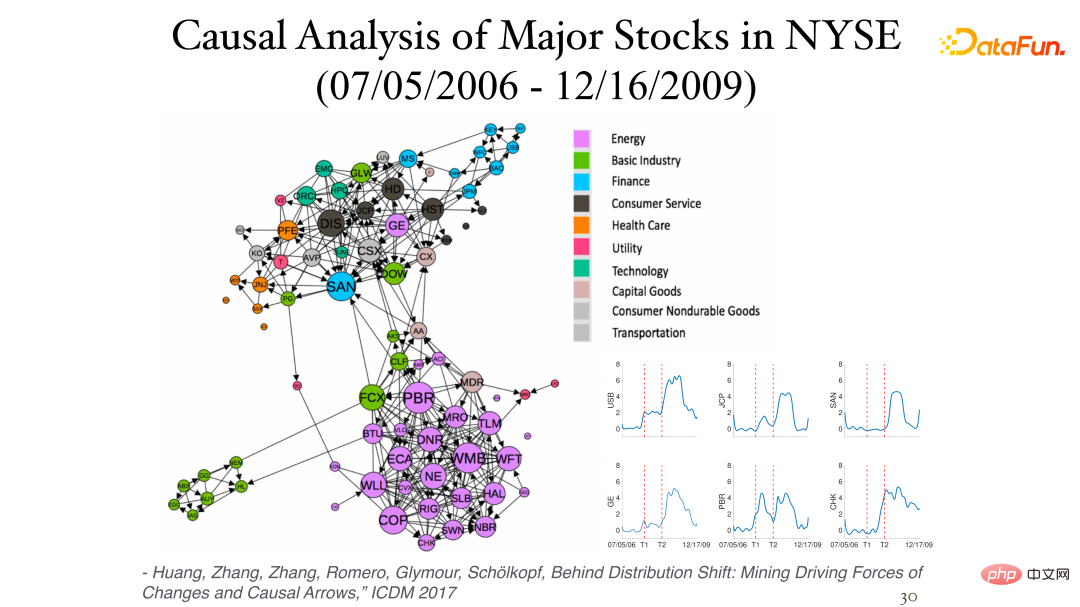

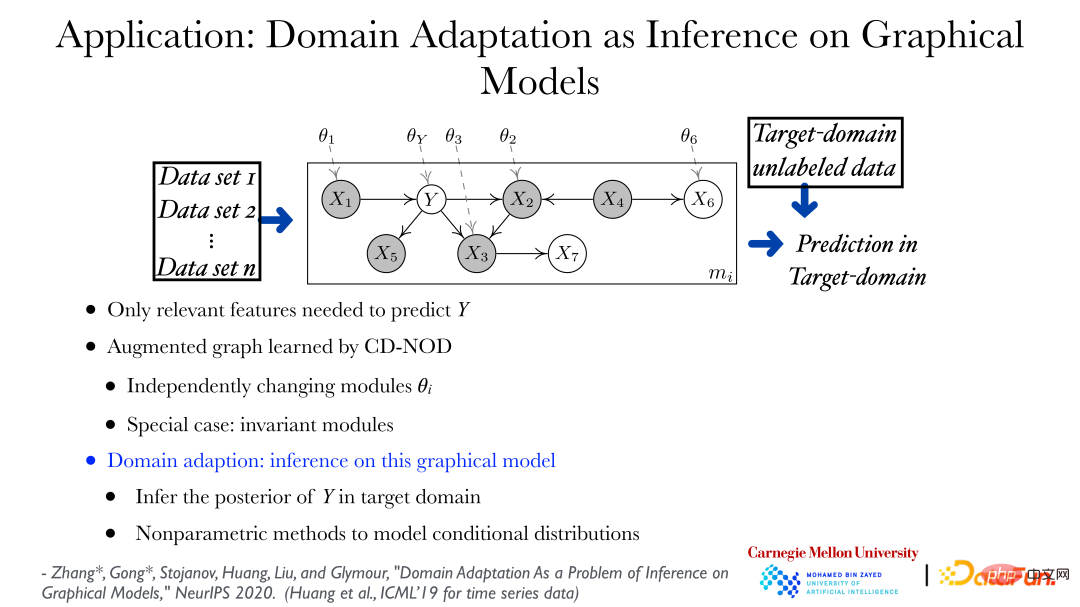
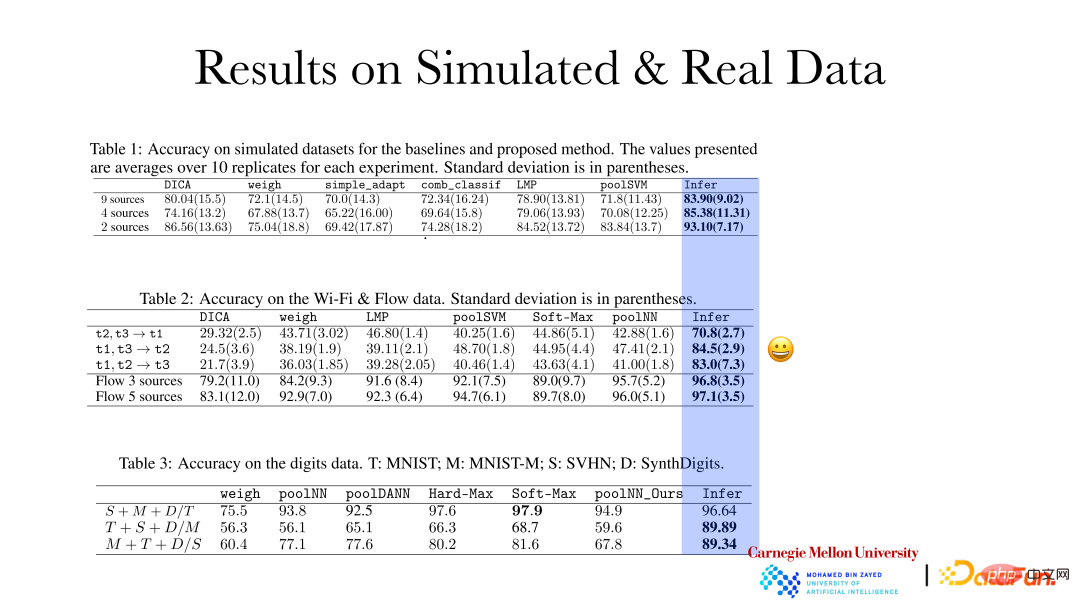
Melalui kaedah analisis sebab di bawah keadaan berbilang pengedaran, corak perubahan data boleh didapati daripada set data yang berbeza Pembelajaran pemindahan boleh dijalankan melalui aplikasi dan domain secara langsung penyesuaian). Seperti yang ditunjukkan dalam rajah di atas, anda boleh mengetahui peraturan perubahan data daripada set data yang berbeza, dan menggunakan graf tambahan untuk menunjukkan bagaimana taburan data boleh berubah Dalam rajah, theta_Y mewakili, Y memberikannya Taburan di bawah nod induk boleh berubah mengikut domainnya. Berdasarkan graf yang menerangkan perubahan dalam taburan data, meramalkan Y dalam medan baru atau medan sasaran adalah masalah yang sangat standard, iaitu, bagaimana untuk mencari kebarangkalian posterior Y memandangkan nilai ciri adalah masalah inferens.

Rajah di atas menunjukkan bahawa ketepatan kesan penaakulan kaedah perwakilan sebab pada data simulasi dan data sebenar telah dipertingkatkan dengan ketara. Berdasarkan peraturan perubahan kualitatif dan magnitud kebolehubahan dalam bidang yang berbeza, pelarasan penyesuaian akan dibuat apabila medan baharu muncul Kesan ramalan jenis ini akan menjadi lebih baik.

Rajah di atas menunjukkan kerja terbaru yang berkaitan dengan Penyelesaian Separa untuk Penyesuaian Domain. Memandangkan ciri dan sasaran, anggap semuanya bukan parametrik, dan beberapa faktor tidak berubah dengan domain, iaitu, pengedaran adalah stabil, tetapi beberapa faktor mungkin berubah. Berdasarkan faktor yang ditemui, bidang yang berbeza boleh diselaraskan bersama-sama, dan kemudian hubungan yang sepadan antara bidang yang berbeza boleh ditemui, supaya penyesuaian domain/pembelajaran pemindahan akan menjadi satu perkara yang pasti. Ia boleh dibuktikan bahawa faktor bebas di sebalik perubahan dalam pengedaran boleh dipulihkan secara langsung daripada data pemerhatian, dan faktor yang tidak berubah boleh memulihkan subruangnya. Seperti yang ditunjukkan dalam jadual, kaedah di atas boleh mencapai hasil yang baik dalam penyesuaian domain. Pada masa yang sama, kaedah ini juga mematuhi prinsip perubahan minimum, iaitu, diharapkan menggunakan faktor yang paling tidak berubah untuk menerangkan bagaimana faktor data dalam bidang yang berbeza telah berubah, supaya sepadan dengannya.

Ringkasnya, perkongsian ini terutamanya termasuk kandungan berikut:

① Satu siri masalah pembelajaran mesin memerlukan perwakilan yang sesuai bagi data di belakangnya. Sebagai contoh, semasa membuat keputusan, anda ingin mengetahui kesan keputusan tersebut, supaya anda boleh membuat keputusan yang optimum dalam penyesuaian/penggeneran domain, anda ingin tahu bagaimana pengedaran data telah berubah, supaya dapat dibuat ramalan optimum; dalam pembelajaran pengukuhan, ejen Interaksi dengan persekitaran dan ganjaran yang dibawa oleh interaksi itu sendiri adalah masalah sebab akibat, kerana pengguna boleh dipercayai, AI yang boleh dijelaskan; keadilan semuanya berkaitan dengan perwakilan kausal.

② Kausaliti, termasuk pembolehubah tersembunyi, boleh dipulihkan sepenuhnya daripada data dalam keadaan tertentu. Anda benar-benar boleh memahami sifat proses di belakangnya melalui data dan kemudian menggunakannya.

③ Kausalitas bukanlah satu misteri. Selagi ada data dan hipotesis sesuai, sebab musabab di sebaliknya boleh ditemui. Andaian yang dibuat di sini sepatutnya boleh diuji.

Secara umumnya, pembelajaran perwakilan sebab mempunyai prospek aplikasi yang hebat Pada masa yang sama, terdapat banyak kaedah yang perlu dibangunkan segera dan memerlukan usaha bersama oleh semua orang.

Atas ialah kandungan terperinci CMU Zhang Kun: Kemajuan terkini dalam teknologi perwakilan sebab. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!