Andrew Ng: Enam algoritma teras pembelajaran mesin

Artikel ini diterbitkan semula daripada Lei Feng.com Jika anda perlu mencetak semula, sila pergi ke tapak web rasmi Lei Feng.com untuk memohon kebenaran.
Baru-baru ini, Andrew Ng mengemas kini catatan blog tentang "The Batch," surat berita kecerdasan buatan mingguan yang diasaskannya, meringkaskan asal-usul sejarah pelbagai algoritma asas dalam bidang pembelajaran mesin. Pada permulaan artikel, Andrew Ng mengimbas kembali keputusan yang dibuatnya dalam proses penyelidikannya: Bertahun-tahun yang lalu, dalam projek, apabila memilih algoritma, dia terpaksa memilih antara rangkaian saraf dan algoritma pembelajaran pokok keputusan. Memandangkan belanjawan pengiraan, dia akhirnya memilih rangkaian saraf, meninggalkan pepohon keputusan yang dirangsang untuk masa yang lama. Ini adalah keputusan yang salah "Nasib baik, pasukan saya segera menyemak pilihan saya dan projek itu berjaya," kata Ng. Beliau mengeluh bahawa adalah sangat penting untuk terus belajar dan mengemaskini pengetahuan asas. Seperti bidang teknikal lain, bidang pembelajaran mesin sentiasa berkembang apabila bilangan penyelidik bertambah dan bilangan hasil penyelidikan bertambah. Tetapi sumbangan beberapa algoritma asas dan idea teras boleh bertahan dalam ujian masa:
- Algoritma: regresi linear dan logistik, pepohon keputusan, dsb.
- Konsep: regularisasi, fungsi kehilangan pengoptimuman, bias/variance, dsb.
Pada pandangan Ng, algoritma dan konsep ini merupakan idea teras banyak mesin model pembelajaran termasuk peramal harga rumah, penjana imej teks (seperti DALL·E), dsb. Dalam artikel terbaru ini, Andrew Ng dan pasukannya menyiasat asal-usul, kegunaan, evolusi, dsb. enam algoritma asas, dan memberikan penjelasan yang lebih terperinci. Enam algoritma tersebut ialah: regresi linear, regresi logistik, keturunan kecerunan, rangkaian saraf, pepohon keputusan dan algoritma k-means clustering.
1 Regresi Linear: Lurus & Sempit
Regresi linear ialah kaedah statistik utama dalam pembelajaran mesin, tetapi ia tidak menang tanpa perlawanan. Ia telah dicadangkan oleh dua ahli matematik yang cemerlang, tetapi 200 tahun kemudian, masalah itu masih tidak dapat diselesaikan. Kontroversi lama menunjukkan bukan sahaja kegunaan algoritma yang luar biasa, tetapi juga kesederhanaan pentingnya.
Jadi algoritma siapakah regresi linear? Pada tahun 1805, ahli matematik Perancis Adrien-Marie Legendre menerbitkan kaedah untuk memasang garis pada satu set titik sambil cuba meramalkan kedudukan komet (navigasi cakerawala adalah arah saintifik yang paling berharga dalam perdagangan global pada masa itu, sama seperti kecerdasan buatan hari ini . pintar).

Kapsyen: Lakaran potret Adrien-Marie LegendreEmpat tahun kemudian, 24 tahun- keajaiban Jerman lama Carl Friedrich Gauss menegaskan bahawa dia telah menggunakannya sejak 1795 tetapi menganggapnya terlalu remeh untuk ditulis. Tuntutan Gauss mendorong Legendre untuk menerbitkan tanpa nama, dengan menyatakan bahawa "seorang geometer yang sangat terkenal menggunakan kaedah ini tanpa teragak-agak >
Ilustrasi: Carl Friedrich GaussCerun dan Sisihan<.>: Regresi linear adalah mudah apabila hubungan antara hasil dan pembolehubah yang mempengaruhinya mengikut garis lurus ia berfungsi. Sebagai contoh, penggunaan bahan api kereta adalah berkaitan secara linear dengan beratnya. Dua langkah untuk mempopularkan: Algoritma serta-merta membantu pelayar menjejaki bintang, serta ahli biologi kemudiannya (terutamanya Charles Darwin) Sepupu Francis Galton) yang dikenal pasti ciri-ciri yang diwarisi dalam tumbuhan dan haiwan. Kedua-dua perkembangan selanjutnya ini membuka kunci potensi luas regresi linear. Pada tahun 1922, ahli statistik British Ronald Fisher dan Karl Pearson menunjukkan bagaimana regresi linear boleh dimuatkan ke dalam rangka kerja statistik umum korelasi dan pengedaran, menjadikannya berguna dalam semua sains. Dan, hampir satu abad kemudian, kemunculan komputer memberikan data dan kuasa pemprosesan untuk mengeksploitasinya ke tahap yang lebih besar. Menangani Kekaburan: Sudah tentu, data tidak pernah diukur dengan sempurna dan sesetengah pembolehubah adalah lebih penting daripada yang lain. Fakta kehidupan ini memberi inspirasi kepada variasi yang lebih kompleks. Sebagai contoh, regresi linear dengan regularisasi (juga dikenali sebagai "regresi rabung") menggalakkan model regresi linear untuk tidak terlalu bergantung pada mana-mana satu pembolehubah, atau lebih tepat, untuk bergantung sama rata pada pembolehubah yang paling penting. Jika untuk kesederhanaan, satu lagi bentuk regularisasi (L1 dan bukannya L2) menghasilkan laso (anggaran termampat) yang menggalakkan seberapa banyak pekali yang mungkin menjadi sifar. Dalam erti kata lain, ia belajar untuk memilih pembolehubah dengan kuasa ramalan yang tinggi dan mengabaikan yang lain. Rangkaian anjal menggabungkan kedua-dua jenis regularisasi ini. Ia berguna apabila data jarang atau apabila ciri kelihatan berkaitan. Dalam setiap neuron : Kini, versi ringkas masih sangat berguna. Jenis neuron yang paling biasa dalam rangkaian saraf ialah model regresi linear, diikuti dengan fungsi pengaktifan bukan linear, menjadikan regresi linear sebagai komponen asas pembelajaran mendalam. Ada masanya regresi logistik hanya digunakan untuk mengklasifikasikan satu perkara: jika anda minum sebotol racun, anda Adalah adakah mungkin untuk dilabel "hidup" atau "mati"? Masa telah berubah, dan hari ini, bukan sahaja panggilan perkhidmatan kecemasan memberikan jawapan yang lebih baik kepada soalan ini, tetapi regresi logistik juga merupakan teras pembelajaran mendalam. Kawalan Racun: Fungsi logistik bermula pada tahun 1830-an, apabila ahli statistik Belgium P.F Verhulst menciptanya untuk menggambarkan dinamik populasi: pertumbuhan eksponen dari semasa ke semasa Ledakan awal tahap pertumbuhan berkurangan kerana ia menggunakan sumber yang ada, menghasilkan keluk logistik yang berciri. Lebih daripada satu abad kemudian, ahli statistik Amerika E. B. Wilson dan pelajarnya Jane Worcester mencipta regresi logistik untuk mengira berapa banyak bahan berbahaya yang diberikan boleh membawa maut. Kapsyen: P.F. VerhulstFungsi pemasangan: regresi logistik Fit a fungsi logistik kepada set data untuk meramalkan kebarangkalian hasil tertentu (cth., kematian pramatang) untuk kejadian tertentu (cth., pengambilan strychnine). Lebih banyak hasil : Kerja Verhulst mendapati kebarangkalian hasil binari, mengabaikan kemungkinan selanjutnya seperti mangsa keracunan mungkin memasuki sisi mana kehidupan akhirat. Penggantinya melanjutkan algoritma: Kapsyen: David CoxKeluk Pelbagai Fungsi : Logistik fungsi menerangkan pelbagai fenomena dengan ketepatan yang tinggi, jadi regresi logistik menyediakan ramalan garis dasar yang berguna dalam banyak situasi. Dalam bidang perubatan, ia menganggarkan risiko kematian dan penyakit. Dalam sains politik, ia meramalkan pemenang dan kalah dalam pilihan raya. Dalam ekonomi, ia meramalkan prospek perniagaan. Lebih penting lagi, ia memacu subset neuron dalam pelbagai rangkaian neural (di mana ketaklinearan ialah fungsi sigmoid). Keturunan Kecerunan 3: Segala-galanya Menurun Bayangkan mendaki di pergunungan selepas senja dan menyedari anda tidak dapat melihat apa-apa di bawah anda. Dan bateri telefon anda mati, jadi anda tidak boleh menggunakan apl GPS anda untuk mencari jalan pulang. Anda mungkin menemui laluan terpantas melalui penurunan kecerunan. Berhati-hati untuk tidak keluar dari tebing. Matahari dan Permaidani: Turun kecerunan lebih berfaedah daripada menuruni rupa bumi yang curam. Pada tahun 1847, ahli matematik Perancis Augustin-Louis Cauchy mencipta algoritma untuk menghampiri orbit bintang. Enam puluh tahun kemudian, rakan senegaranya Jacques Hadamard telah membangunkannya secara bebas untuk menggambarkan ubah bentuk objek nipis dan fleksibel, seperti permaidani, yang mungkin memudahkan pendakian ke bawah lutut. Walau bagaimanapun, dalam pembelajaran mesin, penggunaan yang paling biasa adalah untuk mencari titik terendah fungsi kehilangan algoritma pembelajaran. Kapsyen: Augustin-Louis CauchyNaik turun: Seorang yang terlatih rangkaian saraf menyediakan fungsi yang mengira keluaran yang dikehendaki diberikan input. Satu cara untuk melatih rangkaian adalah untuk meminimumkan kehilangan, atau ralat, dalam output dengan mengira secara berulang perbezaan antara output sebenar dan output yang dikehendaki, dan kemudian menukar nilai parameter rangkaian untuk mengurangkan perbezaan. Keturunan kecerunan mengurangkan perbezaan, meminimumkan fungsi yang mengira kerugian. Nilai parameter rangkaian adalah bersamaan dengan kedudukan pada rupa bumi, dan kerugian ialah ketinggian semasa. Semasa anda turun, anda boleh meningkatkan keupayaan rangkaian untuk mengira sesuatu yang hampir dengan output yang diingini. Keterlihatan adalah terhad kerana dalam situasi pembelajaran biasa yang diselia, algoritma hanya bergantung pada nilai parameter rangkaian dan kecerunan atau kecerunan fungsi kehilangan - iaitu di mana anda berada di atas bukit dan cerun di bawah anda. Terperangkap di Lembah : Sayang sekali telefon anda kehabisan bateri kerana algoritma mungkin tidak mendorong anda ke bahagian bawah gunung. Anda boleh terperangkap dalam landskap tidak cembung yang terdiri daripada berbilang lembah (minima tempatan), puncak (maksimum tempatan), mata pelana (mata pelana) dan dataran tinggi. Sebenarnya, tugas seperti pengecaman imej, penjanaan teks dan pengecaman pertuturan semuanya bukan cembung, dan banyak variasi keturunan kecerunan telah muncul untuk menangani situasi ini. Sebagai contoh, algoritma mungkin mempunyai momentum yang membantu ia menguatkan turun naik kecil, menjadikannya lebih cenderung untuk mencapai bahagian bawah. Para penyelidik mencipta begitu banyak variasi sehingga nampaknya terdapat banyak pengoptimum berbanding minima tempatan. Mujurlah, minima tempatan dan minima global cenderung lebih kurang sama. Pengoptimum optimum: Keturunan kecerunan ialah pilihan yang jelas untuk mencari minimum mana-mana fungsi. Dalam kes di mana penyelesaian tepat boleh dikira secara langsung - contohnya, dalam tugas regresi linear dengan bilangan pembolehubah yang besar - ia boleh menghampiri nilai dan selalunya lebih cepat dan lebih murah. Tetapi ia berguna dalam tugas bukan linear yang kompleks. Dengan keturunan gradien dan rasa pengembaraan, anda mungkin boleh keluar dari pergunungan tepat pada waktunya untuk makan malam. Mari kita selesaikan perkara ini dahulu: Otak bukanlah satu set unit pemprosesan grafik, jika ia Jika ya, perisian yang dijalankannya jauh lebih kompleks daripada rangkaian neural tiruan biasa. Rangkaian saraf diilhamkan oleh struktur otak: lapisan neuron yang saling berkait, masing-masing mengira outputnya sendiri berdasarkan keadaan jirannya Rantaian aktiviti yang terhasil membentuk idea—atau mengenali idea. Dari biologi kepada tiruan: Idea bahawa otak belajar melalui interaksi antara neuron bermula sejak 1873, tetapi tidak sehingga 1943 ahli sains saraf Amerika Warren McCulloch dan Walter Pitts menggunakan peraturan matematik mudah untuk membina model rangkaian saraf biologi. Pada tahun 1958, ahli psikologi Amerika Frank Rosenblatt membangunkan sensor, rangkaian visual satu lapisan yang dilaksanakan pada mesin kad tebuk, dengan matlamat membina versi perkakasan untuk Tentera Laut A.S. Kapsyen: Frank RosenblattLebih besar adalah lebih baik: Ciptaan Rosenblatt boleh hanya mengenali klasifikasi baris tunggal. Kemudian, ahli matematik Ukraine Alexey Ivakhnenko dan Valentin Lapa mengatasi had ini dengan menyusun rangkaian neuron dalam sebarang bilangan lapisan. Pada tahun 1985, saintis komputer Perancis Yann LeCun, David Parker, dan ahli psikologi Amerika David Rumelhart dan rakan sekerja, bekerja secara bebas, menerangkan penggunaan rambatan belakang untuk melatih rangkaian sedemikian dengan berkesan. Dalam dekad pertama alaf baharu, penyelidik termasuk Kumar Chellapilla, Dave Steinkraus dan Rajat Raina (dengan kerjasama Andrew Ng) mendorong lebih jauh lagi dengan menggunakan unit pemprosesan grafik pembangunan rangkaian saraf, yang membolehkan rangkaian saraf yang lebih besar dan lebih besar untuk belajar daripada sejumlah besar data yang dihasilkan oleh Internet. Cocok untuk setiap tugas : Prinsip di sebalik rangkaian saraf adalah mudah: untuk sebarang tugas, terdapat fungsi yang melaksanakannya. Rangkaian saraf membentuk fungsi yang boleh dilatih dengan menggabungkan berbilang fungsi mudah, setiap satu dilakukan oleh neuron tunggal. Fungsi neuron ditentukan oleh parameter boleh laras yang dipanggil "berat". Memandangkan pemberat dan nilai rawak ini untuk contoh input dan output yang diingini, anda boleh menukar pemberat secara berulang sehingga fungsi yang boleh dilatih melaksanakan tugas di tangan. Kotak Hitam: Walaupun dengan apa-apa nasib rangkaian yang terlatih boleh melakukan tugasnya, akhirnya anda akhirnya membaca fungsi yang selalunya Ia sangat kompleks — mengandungi beribu-ribu pembolehubah dan fungsi pengaktifan bersarang — bahawa sukar untuk menerangkan cara rangkaian berjaya dalam tugasnya. Tambahan pula, rangkaian yang terlatih hanya sebaik data yang dipelajarinya. Sebagai contoh, jika set data adalah berat sebelah, maka output rangkaian juga akan menjadi berat sebelah. Jika ia hanya mengandungi imej kucing beresolusi tinggi, tidak diketahui bagaimana ia akan bertindak balas terhadap imej resolusi rendah. Sekeping akal: The New York Times menjejaki gembar-gembur AI apabila ia melaporkan pada sensor Rosenblatt pada tahun 1958, dengan menyatakan bahawa "Tentera Laut A.S. mahukan mesin yang boleh berjalan, bercakap, melihat, menulis dan meniru dirinya sendiri." prototaip komputer elektronik yang menyedari kewujudannya sendiri Walaupun penderia pada masa itu tidak memenuhi keperluan ini, ia menghasilkan banyak model yang mengagumkan: rangkaian saraf konvolusi untuk imej yang berulang untuk teks , pengubah untuk pertuturan, video, struktur protein, dsb. Mereka sudah melakukan perkara yang menakjubkan, seperti melebihi prestasi peringkat manusia semasa bermain Go dan mendekati prestasi peringkat manusia dalam tugas praktikal seperti mendiagnosis imej X-ray. Walau bagaimanapun, mereka masih lebih sukar untuk ditangani dari segi akal dan penaakulan logik. Apakah jenis "binatang" Aristotle? Porphyry, seorang pengikut ahli falsafah yang tinggal di Syria pada abad ketiga, datang dengan cara yang logik untuk menjawab soalan ini. Beliau menggabungkan "kategori kewujudan" yang dicadangkan oleh Aristotle daripada umum kepada khusus, dan mengklasifikasikan Aristotle ke dalam setiap kategori secara bergilir-gilir: Kewujudan Aristotle Dodd adalah material dan bukannya konseptual atau rohani; adalah bernyawa dan bukannya tidak bernyawa; pemikirannya adalah rasional dan bukannya tidak rasional. Oleh itu, klasifikasinya adalah manusia. Guru logik zaman pertengahan melukis urutan ini sebagai gambar rajah aliran menegak: pokok keputusan awal. Perbezaan dalam Nombor: Maju pantas ke 1963, apabila ahli sosiologi Universiti Michigan John Sonquist dan ahli ekonomi James Morgan mengumpulkan responden tinjauan dilaksanakan buat kali pertama dalam komputer. Kerja seperti ini telah menjadi biasa dengan kemunculan perisian yang melatih algoritma secara automatik, dan pepohon keputusan kini digunakan oleh pelbagai perpustakaan pembelajaran mesin termasuk scikit-learn dan lain-lain. Kod ini dibangunkan dalam tempoh 10 tahun oleh empat ahli statistik di Universiti Stanford dan Universiti California, Berkeley. Pada masa ini, menulis pepohon keputusan dari awal telah menjadi tugasan kerja rumah Pembelajaran Mesin 101. Akar di udara: Pokok keputusan boleh melakukan pengelasan atau regresi. Ia tumbuh ke bawah, dari akar ke mahkota, mengklasifikasikan contoh input hierarki keputusan kepada dua (atau lebih). Topik saintis perubatan dan antropologi Jerman Johann Blumenbach terlintas di fikiran: sekitar tahun 1776, dia mula-mula membezakan monyet daripada beruk (meninggalkan manusia sebelum itu, monyet dan beruk dikumpulkan bersama). Pengkelasan ini bergantung kepada pelbagai kriteria, seperti sama ada ia mempunyai ekor, sama ada ia mempunyai dada yang sempit atau lebar, sama ada ia tegak atau membongkok, dan tahap kecerdasannya. Gunakan pokok keputusan terlatih untuk melabelkan haiwan tersebut, dengan mengambil kira setiap kriteria satu demi satu, dan akhirnya memisahkan dua kumpulan haiwan tersebut. Ke dalam 10 Teratas: Memandangkan kesimpulan Blumenbach (kemudian dibatalkan oleh Charles Darwin) bahawa manusia dibezakan daripada beruk melalui pelvis, tangan, dan giginya yang besar, Bagaimana jika kita mahu memanjangkan pokok keputusan untuk mengklasifikasikan bukan sahaja beruk dan monyet, tetapi manusia? Saintis komputer Australia John Ross Quinlan membuat ini mungkin pada tahun 1986 dengan ID3, yang melanjutkan pokok keputusan untuk menyokong hasil bukan binari. Pada tahun 2008, dalam senarai sepuluh algoritma perlombongan data teratas yang dirancang oleh Persidangan Perlombongan Data Antarabangsa IEEE, algoritma pemurnian lanjutan bernama C4.5 menduduki tempat teratas. Dalam dunia di mana inovasi berleluasa, ini adalah kuasa yang kekal. Mengupas daun: Pokok keputusan mempunyai beberapa kelemahan. Mereka boleh melebihkan data dengan mudah dengan menambahkan berbilang peringkat hierarki supaya nod daun hanya merangkumi satu contoh. Apa yang lebih teruk ialah mereka terdedah kepada kesan rama-rama: menukar contoh, pokok yang tumbuh adalah berbeza sama sekali. Ke dalam hutan: Ahli statistik Amerika Leo Breiman dan ahli statistik New Zealand Adele Cutler menjadikan ciri ini sebagai kelebihan dan membangunkan hutan rawak (hutan rawak) pada tahun 2001 - Ini ialah koleksi pokok keputusan , yang setiap satunya memproses pemilihan contoh dan undian yang berbeza dan bertindih pada hasil akhir. Random Forest dan sepupunya XGBoost kurang terdedah kepada overfitting, yang membantu menjadikannya salah satu algoritma pembelajaran mesin yang paling popular. Ia seperti mempunyai Aristotle, Porphyry, Blumenbach, Darwin, Jane Goodall, Dian Fossey dan 1,000 ahli zoologi lain di dalam bilik bersama-sama untuk memastikan klasifikasi anda adalah yang terbaik. Jika anda berdiri rapat dengan orang lain di sebuah parti, kemungkinan besar anda mempunyai persamaan. Ini adalah idea menggunakan k-means clustering untuk mengumpulkan titik data. Sama ada kumpulan yang dibentuk melalui agensi manusia atau kuasa lain, algoritma ini akan menemui mereka. Daripada letupan kepada nada dail: Ahli fizik Amerika Stuart Lloyd, alumnus Kilang Inovasi ikonik Bell Labs dan Projek Manhattan yang mencipta bom atom, mula-mula mencadangkan k-means clustering pada tahun 1957 untuk menganalisis maklumat Peruntukan digital dalam isyarat, tetapi karya ini tidak diterbitkan sehingga 1982: Alamat kertas: https://cs.nyu.edu /~roweis /csc2515-2006/readings/lloyd57.pdfSementara itu, ahli statistik Amerika Edward Forgy menerangkan pendekatan serupa pada tahun 1965, yang membawa kepada nama alternatifnya "Lloyd-Forgy Algorithm". Mencari Hab: Pertimbangkan untuk membahagikan kelompok kepada kumpulan kerja yang berfikiran sama. Memandangkan lokasi peserta di dalam bilik dan bilangan kumpulan untuk dibentuk, k-means clustering boleh membahagikan peserta kepada kumpulan yang bersaiz lebih kurang sama, dengan setiap kumpulan berkumpul di sekeliling titik pusat atau centroid. Jarak yang berbeza: Sudah tentu, jarak antara objek berkelompok tidak perlu besar. Sebarang metrik antara dua vektor akan berjaya. Sebagai contoh, bukannya mengelompokkan pengunjung parti berdasarkan jarak fizikal, k-means clustering boleh membahagikan mereka berdasarkan pakaian, pekerjaan atau atribut lain mereka. Kedai dalam talian menggunakannya untuk membahagikan pelanggan berdasarkan keutamaan atau tingkah laku mereka dan ahli astronomi boleh mengumpulkan bintang daripada jenis yang sama bersama-sama. Kuasa Mata Data: Idea ini menghasilkan beberapa perubahan yang luar biasa: karnival n-dimensi : Namun begitu, algoritma dalam bentuk asalnya masih berguna secara meluas - terutamanya kerana sebagai algoritma tanpa pengawasan ia tidak memerlukan Pengumpulan data berlabel mahal. Ia juga digunakan dengan lebih pantas dan pantas. Contohnya, perpustakaan pembelajaran mesin termasuk scikit-learn mendapat manfaat daripada penambahan kd-trees pada tahun 2002, yang boleh membahagikan data berdimensi tinggi dengan cepat.
2 Regresi Logistik: Mengikuti Keluk

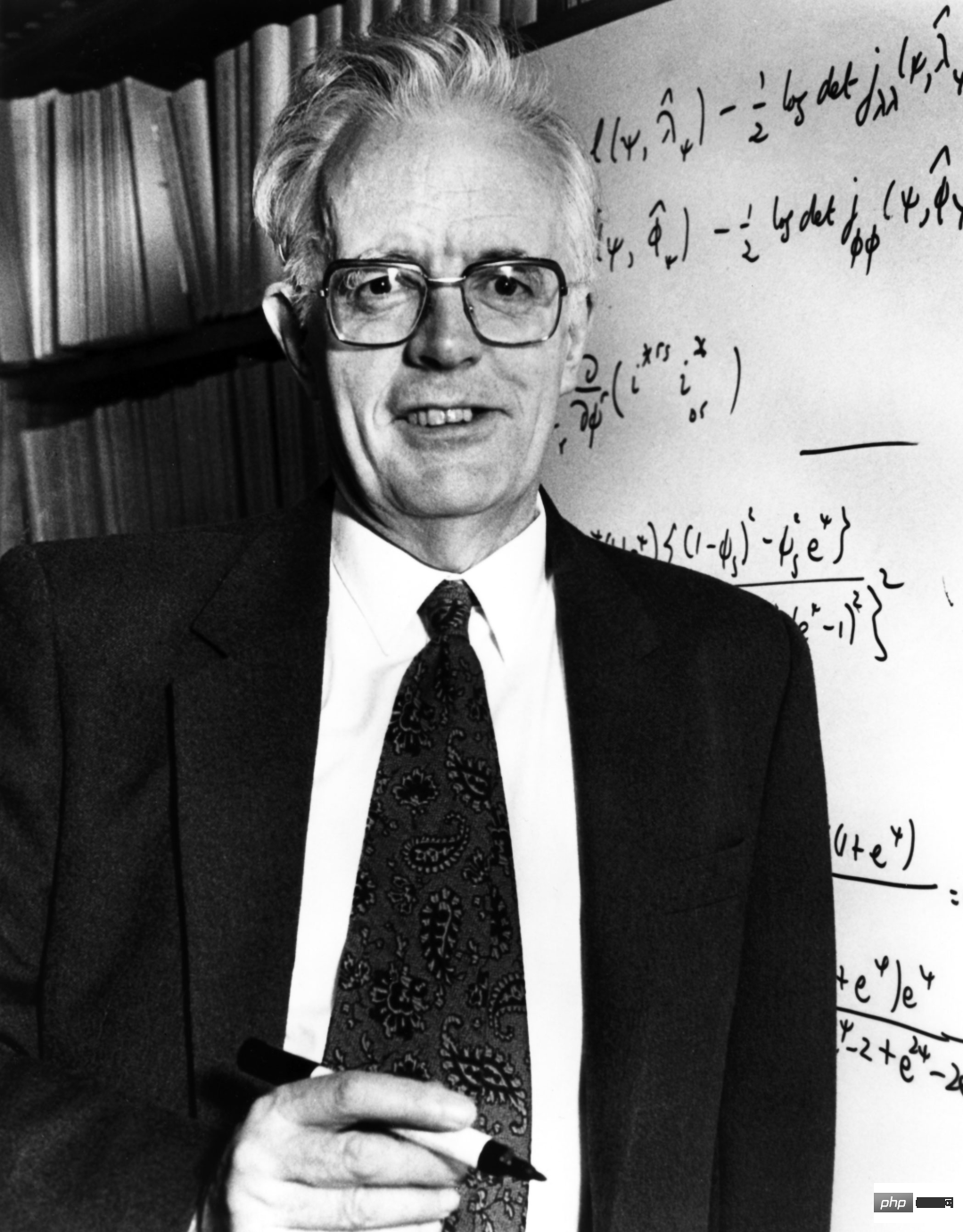
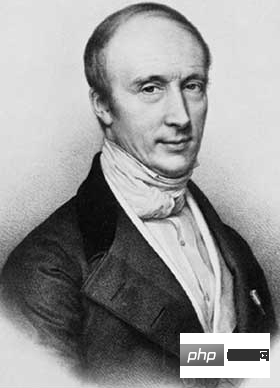
4 Rangkaian Neural: Fungsi Mencari

5 Pokok Keputusan: Dari Akar ke Daun
6 K-Means Clustering: Groupthink
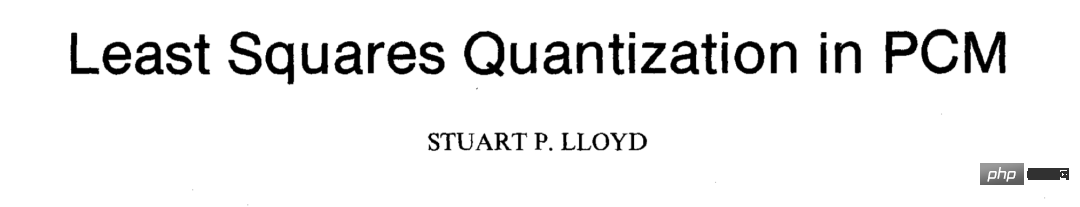
Atas ialah kandungan terperinci Andrew Ng: Enam algoritma teras pembelajaran mesin. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1376
1376
 52
52
 Geospatial Laravel: Pengoptimuman peta interaktif dan sejumlah besar data
Apr 08, 2025 pm 12:24 PM
Geospatial Laravel: Pengoptimuman peta interaktif dan sejumlah besar data
Apr 08, 2025 pm 12:24 PM
Cecair memproses 7 juta rekod dan membuat peta interaktif dengan teknologi geospatial. Artikel ini meneroka cara memproses lebih dari 7 juta rekod menggunakan Laravel dan MySQL dan mengubahnya menjadi visualisasi peta interaktif. Keperluan Projek Cabaran Awal: Ekstrak Wawasan berharga menggunakan 7 juta rekod dalam pangkalan data MySQL. Ramai orang mula -mula mempertimbangkan bahasa pengaturcaraan, tetapi mengabaikan pangkalan data itu sendiri: Bolehkah ia memenuhi keperluan? Adakah penghijrahan data atau pelarasan struktur diperlukan? Bolehkah MySQL menahan beban data yang besar? Analisis awal: Penapis utama dan sifat perlu dikenalpasti. Selepas analisis, didapati bahawa hanya beberapa atribut yang berkaitan dengan penyelesaiannya. Kami mengesahkan kemungkinan penapis dan menetapkan beberapa sekatan untuk mengoptimumkan carian. Carian Peta Berdasarkan Bandar
 Cara menyelesaikan MySQL tidak dapat dimulakan
Apr 08, 2025 pm 02:21 PM
Cara menyelesaikan MySQL tidak dapat dimulakan
Apr 08, 2025 pm 02:21 PM
Terdapat banyak sebab mengapa permulaan MySQL gagal, dan ia boleh didiagnosis dengan memeriksa log ralat. Penyebab umum termasuk konflik pelabuhan (periksa penghunian pelabuhan dan ubah suai konfigurasi), isu kebenaran (periksa keizinan pengguna yang menjalankan perkhidmatan), ralat fail konfigurasi (periksa tetapan parameter), rasuah direktori data (memulihkan data atau membina semula ruang meja), isu ruang jadual InnoDB (semak fail ibdata1) Apabila menyelesaikan masalah, anda harus menganalisisnya berdasarkan log ralat, cari punca utama masalah, dan mengembangkan tabiat sandaran data secara teratur untuk mencegah dan menyelesaikan masalah.
 Cara Menggunakan MySQL Selepas Pemasangan
Apr 08, 2025 am 11:48 AM
Cara Menggunakan MySQL Selepas Pemasangan
Apr 08, 2025 am 11:48 AM
Artikel ini memperkenalkan operasi pangkalan data MySQL. Pertama, anda perlu memasang klien MySQL, seperti MySqlworkbench atau Command Line Client. 1. Gunakan perintah MySQL-Uroot-P untuk menyambung ke pelayan dan log masuk dengan kata laluan akaun root; 2. Gunakan CreateTatabase untuk membuat pangkalan data, dan gunakan Pilih pangkalan data; 3. Gunakan createtable untuk membuat jadual, menentukan medan dan jenis data; 4. Gunakan InsertInto untuk memasukkan data, data pertanyaan, kemas kini data dengan kemas kini, dan padam data dengan padam. Hanya dengan menguasai langkah -langkah ini, belajar menangani masalah biasa dan mengoptimumkan prestasi pangkalan data anda boleh menggunakan MySQL dengan cekap.
 Jurutera Backend Senior Remote (Platform) memerlukan kalangan
Apr 08, 2025 pm 12:27 PM
Jurutera Backend Senior Remote (Platform) memerlukan kalangan
Apr 08, 2025 pm 12:27 PM
Jurutera Backend Senior Remote Company Kekosongan Syarikat: Lokasi Lokasi: Jauh Pejabat Jauh Jenis: Gaji sepenuh masa: $ 130,000- $ 140,000 Penerangan Pekerjaan Mengambil bahagian dalam penyelidikan dan pembangunan aplikasi mudah alih Circle dan ciri-ciri berkaitan API awam yang meliputi keseluruhan kitaran hayat pembangunan perisian. Tanggungjawab utama kerja pembangunan secara bebas berdasarkan rubyonrails dan bekerjasama dengan pasukan react/redux/relay front-end. Membina fungsi teras dan penambahbaikan untuk aplikasi web dan bekerjasama rapat dengan pereka dan kepimpinan sepanjang proses reka bentuk berfungsi. Menggalakkan proses pembangunan positif dan mengutamakan kelajuan lelaran. Memerlukan lebih daripada 6 tahun backend aplikasi web kompleks
 Bolehkah mysql kembali json
Apr 08, 2025 pm 03:09 PM
Bolehkah mysql kembali json
Apr 08, 2025 pm 03:09 PM
MySQL boleh mengembalikan data JSON. Fungsi JSON_EXTRACT mengekstrak nilai medan. Untuk pertanyaan yang kompleks, pertimbangkan untuk menggunakan klausa WHERE untuk menapis data JSON, tetapi perhatikan kesan prestasinya. Sokongan MySQL untuk JSON sentiasa meningkat, dan disyorkan untuk memberi perhatian kepada versi dan ciri terkini.
 Memahami sifat asid: tiang pangkalan data yang boleh dipercayai
Apr 08, 2025 pm 06:33 PM
Memahami sifat asid: tiang pangkalan data yang boleh dipercayai
Apr 08, 2025 pm 06:33 PM
Penjelasan terperinci mengenai atribut asid asid pangkalan data adalah satu set peraturan untuk memastikan kebolehpercayaan dan konsistensi urus niaga pangkalan data. Mereka menentukan bagaimana sistem pangkalan data mengendalikan urus niaga, dan memastikan integriti dan ketepatan data walaupun dalam hal kemalangan sistem, gangguan kuasa, atau pelbagai pengguna akses serentak. Gambaran keseluruhan atribut asid Atomicity: Transaksi dianggap sebagai unit yang tidak dapat dipisahkan. Mana -mana bahagian gagal, keseluruhan transaksi dilancarkan kembali, dan pangkalan data tidak mengekalkan sebarang perubahan. Sebagai contoh, jika pemindahan bank ditolak dari satu akaun tetapi tidak meningkat kepada yang lain, keseluruhan operasi dibatalkan. Begintransaction; UpdateAcCountSsetBalance = Balance-100Wh
 Mysql tidak dapat dipasang setelah memuat turun
Apr 08, 2025 am 11:24 AM
Mysql tidak dapat dipasang setelah memuat turun
Apr 08, 2025 am 11:24 AM
Sebab utama kegagalan pemasangan MySQL adalah: 1. Isu kebenaran, anda perlu menjalankan sebagai pentadbir atau menggunakan perintah sudo; 2. Ketergantungan hilang, dan anda perlu memasang pakej pembangunan yang relevan; 3. Konflik pelabuhan, anda perlu menutup program yang menduduki port 3306 atau mengubah suai fail konfigurasi; 4. Pakej pemasangan adalah korup, anda perlu memuat turun dan mengesahkan integriti; 5. Pembolehubah persekitaran dikonfigurasikan dengan salah, dan pembolehubah persekitaran mesti dikonfigurasi dengan betul mengikut sistem operasi. Selesaikan masalah ini dan periksa dengan teliti setiap langkah untuk berjaya memasang MySQL.
 Kunci utama MySQL boleh menjadi batal
Apr 08, 2025 pm 03:03 PM
Kunci utama MySQL boleh menjadi batal
Apr 08, 2025 pm 03:03 PM
Kunci utama MySQL tidak boleh kosong kerana kunci utama adalah atribut utama yang secara unik mengenal pasti setiap baris dalam pangkalan data. Jika kunci utama boleh kosong, rekod tidak dapat dikenal pasti secara unik, yang akan membawa kepada kekeliruan data. Apabila menggunakan lajur integer sendiri atau UUIDs sebagai kunci utama, anda harus mempertimbangkan faktor-faktor seperti kecekapan dan penghunian ruang dan memilih penyelesaian yang sesuai.





