Sains data yang mesti diketahui: 10 konsep penting + makna 22 carta
01 Bias-variance trade-off
Ini ialah konsep yang sentiasa berada di kedudukan teratas dalam teori pembelajaran mesin yang paling penting. Hampir semua algoritma dalam pembelajaran mesin (termasuk pembelajaran mendalam) berusaha untuk mencapai keseimbangan yang betul antara bias dan varians, dan rajah ini dengan jelas menerangkan tentangan antara kedua-duanya.
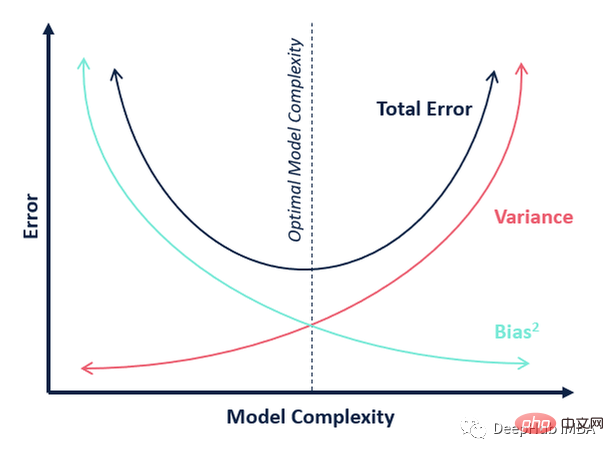
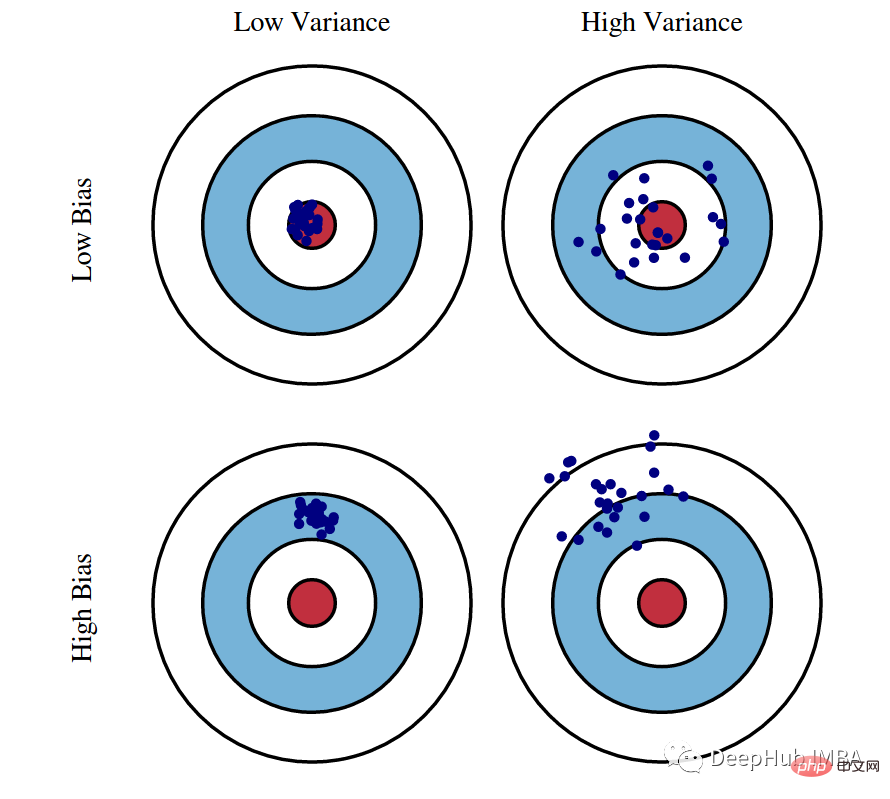
02 Kekotoran dan Entropi Gini
Gini (ukuran kekurangan kehomogenan) dan Entropi (ukuran rawak) adalah kedua-duanya keputusan A ukuran kekotoran nod dalam pokok.
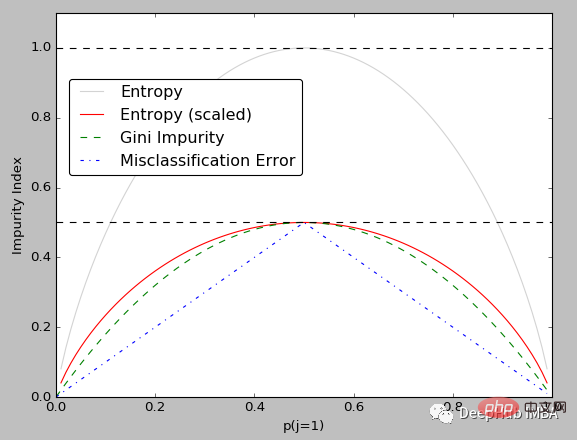

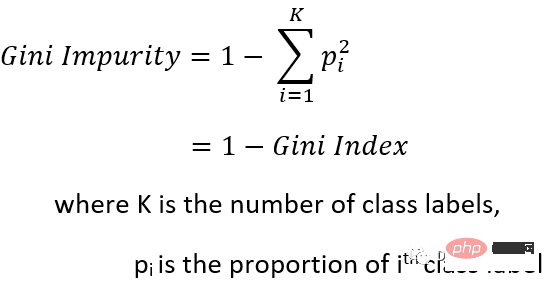
Untuk kedua-dua konsep ini adalah lebih penting untuk memahami hubungan antara mereka supaya dapat memahami hubungan antara mereka dalam yang diberikan Pilih penunjuk yang sesuai untuk senario.
Kekotoran gini (pekali) secara amnya lebih mudah dikira berbanding entropi (kerana entropi melibatkan pengiraan logaritma).
Keluk Precision vs Recall 03
Keluk ingatan kembali ketepatan menunjukkan pertukaran antara ketepatan dan panggil balik untuk ambang yang berbeza. Kawasan besar di bawah lengkung mewakili ingatan tinggi dan ketepatan tinggi, di mana ketepatan tinggi berkaitan dengan kadar penggera palsu yang rendah, dan ingatan semula tinggi berkaitan dengan kadar penggera palsu yang rendah.
Ia boleh membantu kami memilih ambang yang betul mengikut keperluan kami. Sebagai contoh, jika matlamat kita adalah untuk mengurangkan ralat jenis 1, kita perlu memilih ketepatan yang tinggi, manakala jika matlamat kita adalah untuk meminimumkan ralat jenis 2, maka kita harus memilih ambang supaya penarikan balik adalah tinggi. 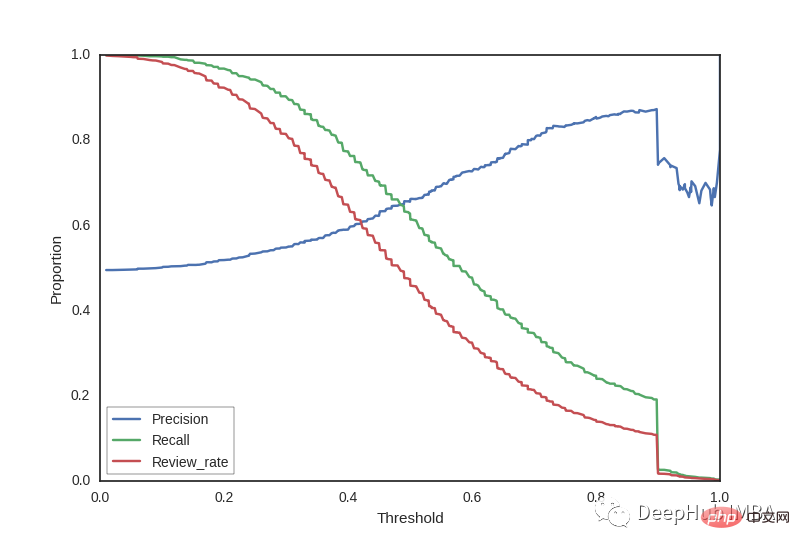
- Penyebut ketepatan ialah pembolehubah: iaitu positif palsu (sampel negatif dikelaskan sebagai positif) akan berubah setiap kali.
- Penyebut ingat semula ialah pemalar: ia mewakili jumlah bilangan nilai sebenar dan oleh itu akan sentiasa kekal sama.
Itulah sebabnya dalam gambar di bawah Precision mempunyai gelombang pada penghujungnya, manakala Recall sentiasa kekal rata.
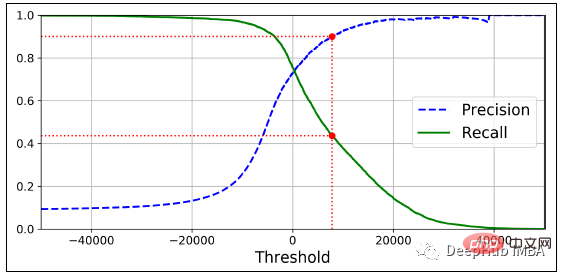
Keluk ROC 04
Keluk ROC ialah graf yang menunjukkan prestasi model pengelasan pada semua ambang pengelasan.
Lengkung ini memplot dua parameter:
真阳性率<br>误报率
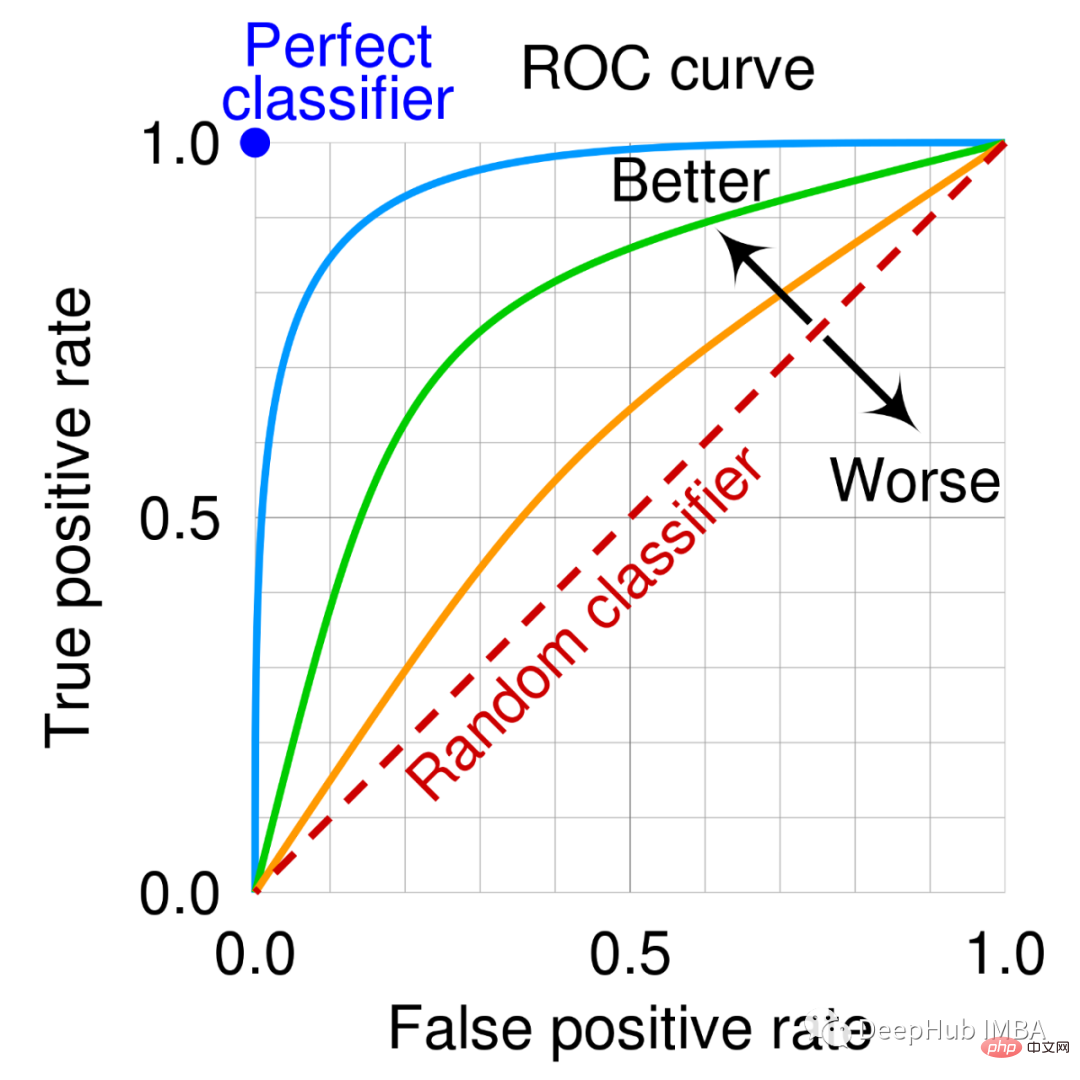
Kawasan di bawah lengkung ini (dipanggil AUC) juga boleh digunakan sebagai metrik prestasi . Lebih tinggi AUC, lebih baik modelnya.
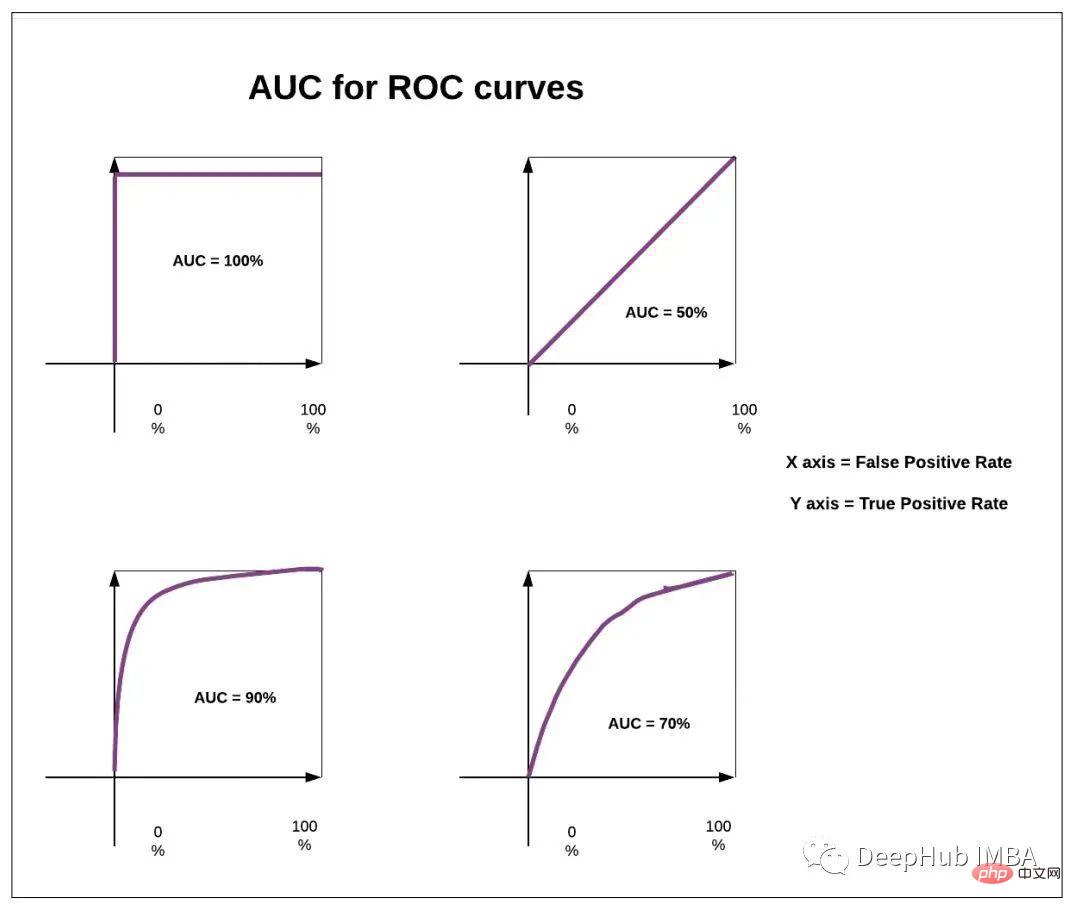
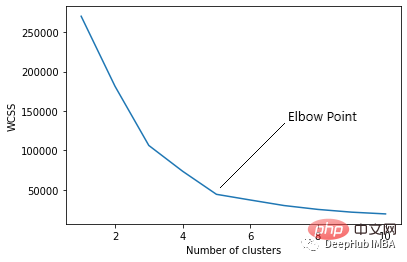
05 弯头曲线
用于K-means算法中最优簇数的选择。WCSS(簇内平方和)是给定簇中每个点与质心之间的平方距离之和。当我们用 K(簇数)值绘制 WCSS 时,该图看起来像一个肘部(弯头)。
随着聚类数量的增加,WCSS 值将开始下降。K = 1时WCSS值最大
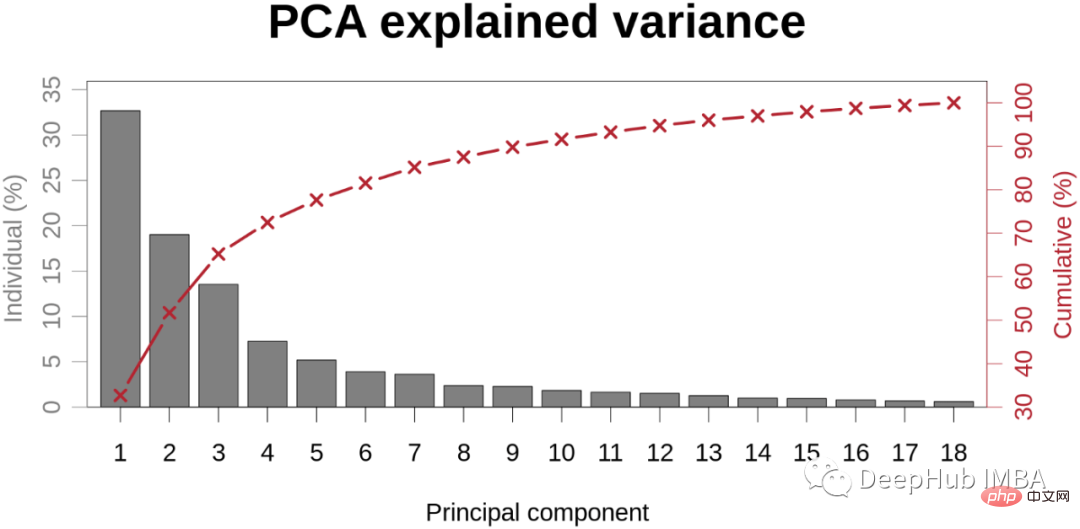
06三块地块
它帮助我们在对高维数据执行主成分分析后,可视化每个主成分解释的变异百分比。为了选择正确数量的主成分来考虑我们的模型,我们通常会绘制此图并选择能够为我们提供足够好的总体方差百分比的值。
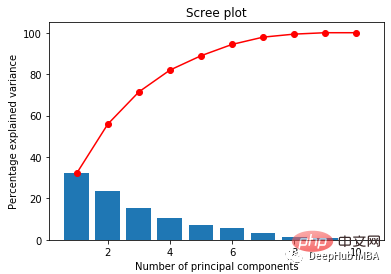
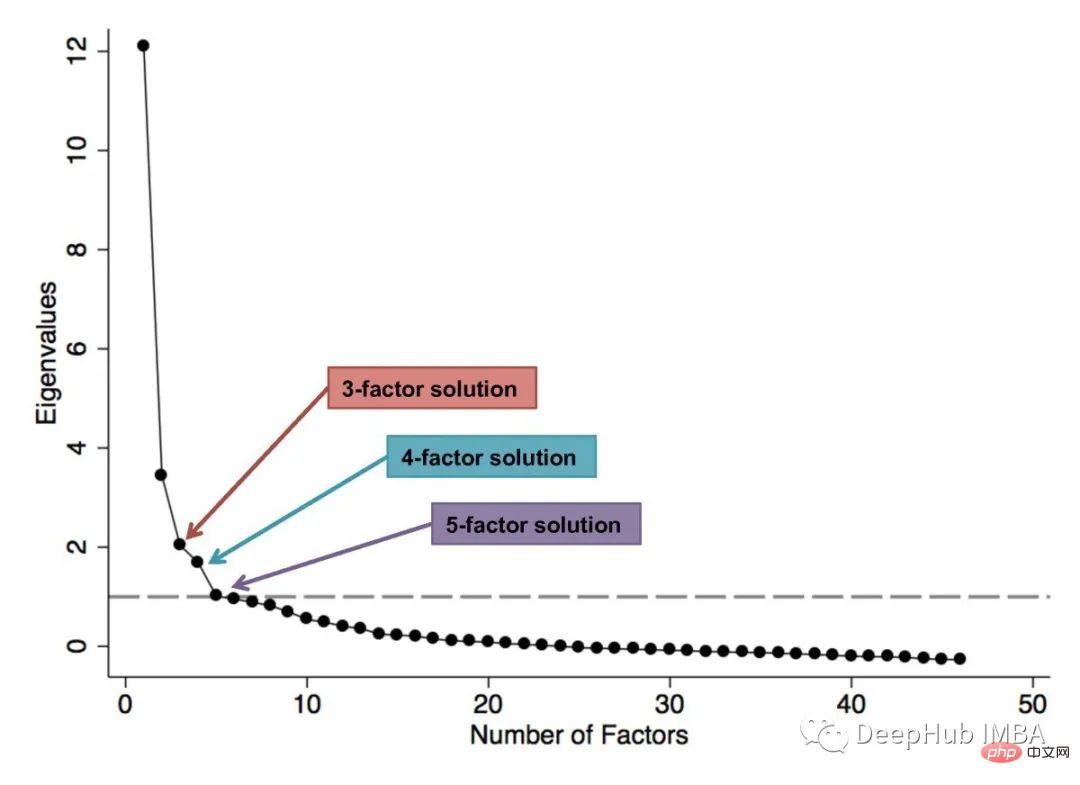
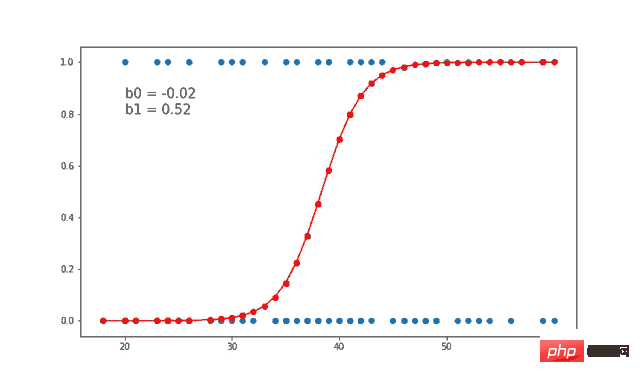
07线性和逻辑回归曲线
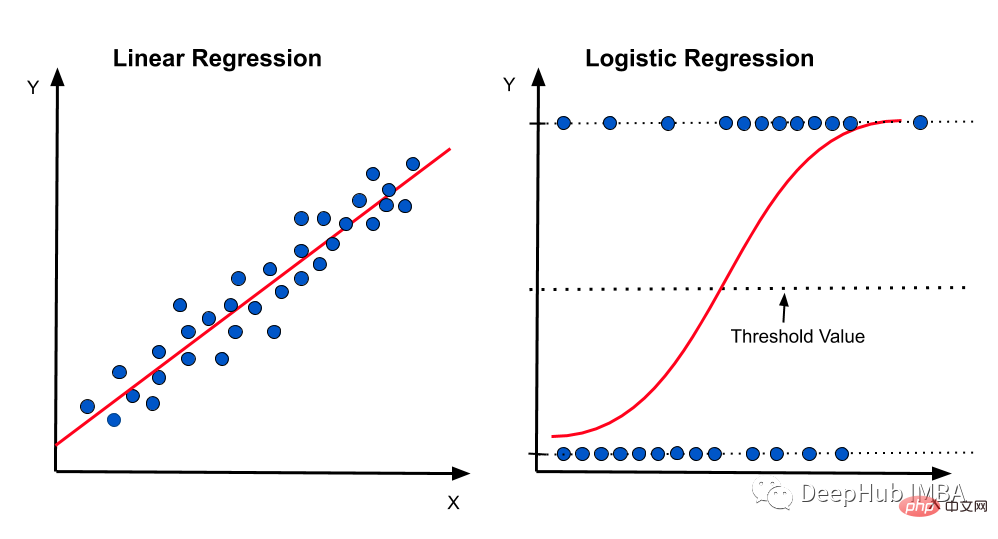
对于线性可分数据,我们可以进行线性回归或逻辑回归,二者都可以作为决策边界曲线/线。但是,在逻辑回归的情况下,由于通常只有 2 个类别,因此具有线性直线决策边界可能不起作用,在一条直线上值从低到高非常均匀地上升,因为它不够陡峭在值突然上升后会得到很多临界的高值或者低值,最终会错误分类。因此,"边界"区域,即概率从高到低转变的区域并不真正存在。所以一般情况下会应用 sigmoid 变换将其转换为 sigmoid 曲线,该曲线在极端情况下是平滑的,在中间几乎是线性的。
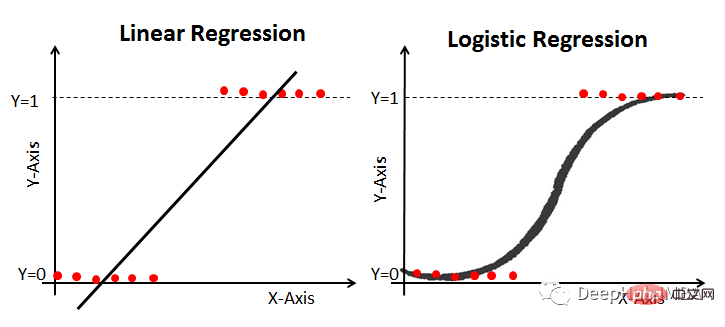
08支持向量机(几何理解)
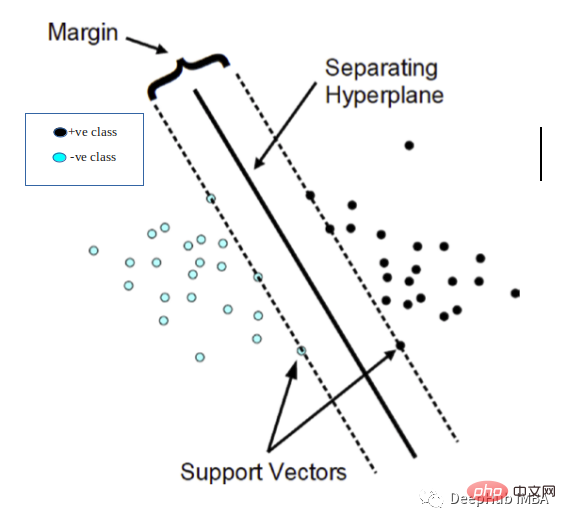
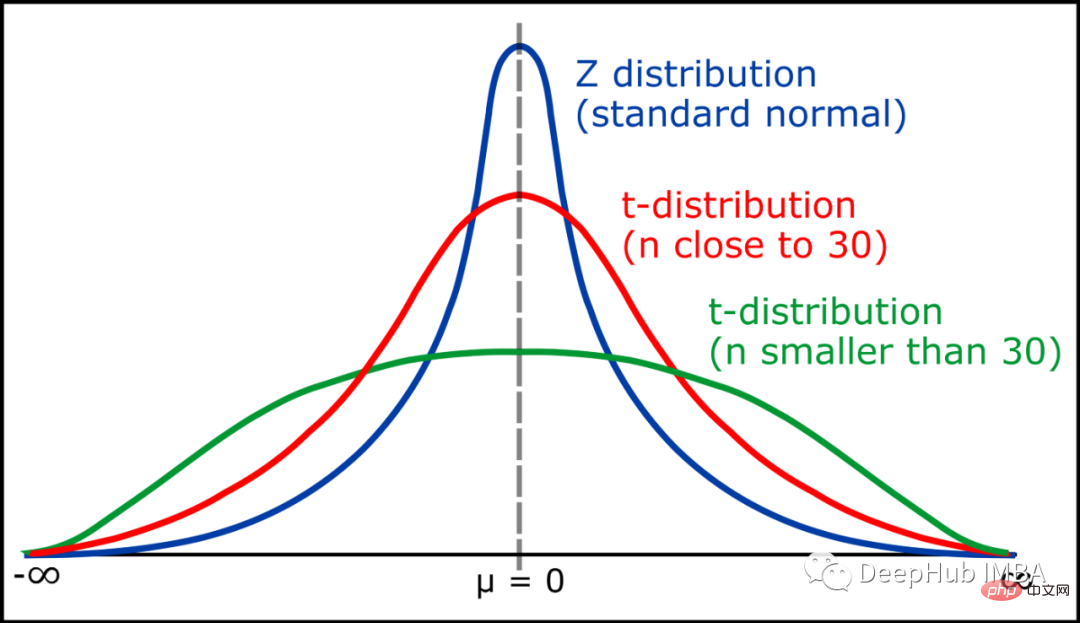
09标准正态分布规则(z-分布)
均值为0,标准差为1的特殊正态分布。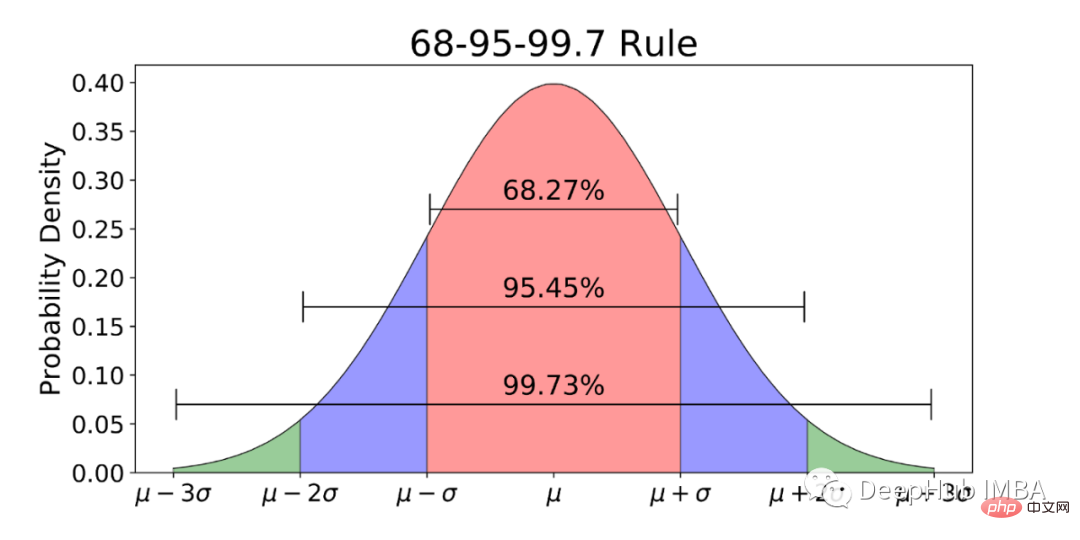
经验法则指出,按照正态分布观察到的数据中有 99.7% 位于平均值的 3 个标准差以内。根据该规则,68% 的数据在一个标准差内,95% 在两个标准差内,99.7% 在三个标准差内。10学生T分布T 分布(也称为学生 T 分布)是一系列分布,看起来几乎与正态分布曲线相同,只是更短和更宽/更胖。当我们有较小的样本时,我们使用 T分布而不是正态分布。样本量越大,t 分布越像正态分布。事实上,在 30 个样本之后,T 分布几乎与正态分布完全一样。
Ringkasan
Kita mungkin terjumpa banyak konsep kecil tetapi kritikal yang menjadi asas untuk kita membuat keputusan atau memilih model yang betul. Konsep-konsep penting yang dinyatakan dalam artikel ini boleh diwakili oleh gambar rajah yang berkaitan konsep-konsep ini adalah sangat penting dan kita perlu mengetahui maksudnya pada kali pertama kita melihatnya gambar mewakili:
Atas ialah kandungan terperinci Sains data yang mesti diketahui: 10 konsep penting + makna 22 carta. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1381
1381
 52
52
 Artikel ini akan membawa anda memahami SHAP: penjelasan model untuk pembelajaran mesin
Jun 01, 2024 am 10:58 AM
Artikel ini akan membawa anda memahami SHAP: penjelasan model untuk pembelajaran mesin
Jun 01, 2024 am 10:58 AM
Dalam bidang pembelajaran mesin dan sains data, kebolehtafsiran model sentiasa menjadi tumpuan penyelidik dan pengamal. Dengan aplikasi meluas model yang kompleks seperti kaedah pembelajaran mendalam dan ensemble, memahami proses membuat keputusan model menjadi sangat penting. AI|XAI yang boleh dijelaskan membantu membina kepercayaan dan keyakinan dalam model pembelajaran mesin dengan meningkatkan ketelusan model. Meningkatkan ketelusan model boleh dicapai melalui kaedah seperti penggunaan meluas pelbagai model yang kompleks, serta proses membuat keputusan yang digunakan untuk menerangkan model. Kaedah ini termasuk analisis kepentingan ciri, anggaran selang ramalan model, algoritma kebolehtafsiran tempatan, dsb. Analisis kepentingan ciri boleh menerangkan proses membuat keputusan model dengan menilai tahap pengaruh model ke atas ciri input. Anggaran selang ramalan model
 Kenal pasti overfitting dan underfitting melalui lengkung pembelajaran
Apr 29, 2024 pm 06:50 PM
Kenal pasti overfitting dan underfitting melalui lengkung pembelajaran
Apr 29, 2024 pm 06:50 PM
Artikel ini akan memperkenalkan cara mengenal pasti pemasangan lampau dan kekurangan dalam model pembelajaran mesin secara berkesan melalui keluk pembelajaran. Underfitting dan overfitting 1. Overfitting Jika model terlampau latihan pada data sehingga ia mempelajari bunyi daripadanya, maka model tersebut dikatakan overfitting. Model yang dipasang terlebih dahulu mempelajari setiap contoh dengan sempurna sehingga ia akan salah mengklasifikasikan contoh yang tidak kelihatan/baharu. Untuk model terlampau, kami akan mendapat skor set latihan yang sempurna/hampir sempurna dan set pengesahan/skor ujian yang teruk. Diubah suai sedikit: "Punca overfitting: Gunakan model yang kompleks untuk menyelesaikan masalah mudah dan mengekstrak bunyi daripada data. Kerana set data kecil sebagai set latihan mungkin tidak mewakili perwakilan yang betul bagi semua data. 2. Underfitting Heru
 Telus! Analisis mendalam tentang prinsip model pembelajaran mesin utama!
Apr 12, 2024 pm 05:55 PM
Telus! Analisis mendalam tentang prinsip model pembelajaran mesin utama!
Apr 12, 2024 pm 05:55 PM
Dalam istilah orang awam, model pembelajaran mesin ialah fungsi matematik yang memetakan data input kepada output yang diramalkan. Secara lebih khusus, model pembelajaran mesin ialah fungsi matematik yang melaraskan parameter model dengan belajar daripada data latihan untuk meminimumkan ralat antara output yang diramalkan dan label sebenar. Terdapat banyak model dalam pembelajaran mesin, seperti model regresi logistik, model pepohon keputusan, model mesin vektor sokongan, dll. Setiap model mempunyai jenis data dan jenis masalah yang berkenaan. Pada masa yang sama, terdapat banyak persamaan antara model yang berbeza, atau terdapat laluan tersembunyi untuk evolusi model. Mengambil perceptron penyambung sebagai contoh, dengan meningkatkan bilangan lapisan tersembunyi perceptron, kita boleh mengubahnya menjadi rangkaian neural yang mendalam. Jika fungsi kernel ditambah pada perceptron, ia boleh ditukar menjadi SVM. yang ini
 Evolusi kecerdasan buatan dalam penerokaan angkasa lepas dan kejuruteraan penempatan manusia
Apr 29, 2024 pm 03:25 PM
Evolusi kecerdasan buatan dalam penerokaan angkasa lepas dan kejuruteraan penempatan manusia
Apr 29, 2024 pm 03:25 PM
Pada tahun 1950-an, kecerdasan buatan (AI) dilahirkan. Ketika itulah penyelidik mendapati bahawa mesin boleh melakukan tugas seperti manusia, seperti berfikir. Kemudian, pada tahun 1960-an, Jabatan Pertahanan A.S. membiayai kecerdasan buatan dan menubuhkan makmal untuk pembangunan selanjutnya. Penyelidik sedang mencari aplikasi untuk kecerdasan buatan dalam banyak bidang, seperti penerokaan angkasa lepas dan kelangsungan hidup dalam persekitaran yang melampau. Penerokaan angkasa lepas ialah kajian tentang alam semesta, yang meliputi seluruh alam semesta di luar bumi. Angkasa lepas diklasifikasikan sebagai persekitaran yang melampau kerana keadaannya berbeza daripada di Bumi. Untuk terus hidup di angkasa, banyak faktor mesti dipertimbangkan dan langkah berjaga-jaga mesti diambil. Para saintis dan penyelidik percaya bahawa meneroka ruang dan memahami keadaan semasa segala-galanya boleh membantu memahami cara alam semesta berfungsi dan bersedia untuk menghadapi kemungkinan krisis alam sekitar
 Melaksanakan Algoritma Pembelajaran Mesin dalam C++: Cabaran dan Penyelesaian Biasa
Jun 03, 2024 pm 01:25 PM
Melaksanakan Algoritma Pembelajaran Mesin dalam C++: Cabaran dan Penyelesaian Biasa
Jun 03, 2024 pm 01:25 PM
Cabaran biasa yang dihadapi oleh algoritma pembelajaran mesin dalam C++ termasuk pengurusan memori, multi-threading, pengoptimuman prestasi dan kebolehselenggaraan. Penyelesaian termasuk menggunakan penunjuk pintar, perpustakaan benang moden, arahan SIMD dan perpustakaan pihak ketiga, serta mengikuti garis panduan gaya pengekodan dan menggunakan alat automasi. Kes praktikal menunjukkan cara menggunakan perpustakaan Eigen untuk melaksanakan algoritma regresi linear, mengurus memori dengan berkesan dan menggunakan operasi matriks berprestasi tinggi.
 AI yang boleh dijelaskan: Menerangkan model AI/ML yang kompleks
Jun 03, 2024 pm 10:08 PM
AI yang boleh dijelaskan: Menerangkan model AI/ML yang kompleks
Jun 03, 2024 pm 10:08 PM
Penterjemah |. Disemak oleh Li Rui |. Chonglou Model kecerdasan buatan (AI) dan pembelajaran mesin (ML) semakin kompleks hari ini, dan output yang dihasilkan oleh model ini adalah kotak hitam – tidak dapat dijelaskan kepada pihak berkepentingan. AI Boleh Dijelaskan (XAI) bertujuan untuk menyelesaikan masalah ini dengan membolehkan pihak berkepentingan memahami cara model ini berfungsi, memastikan mereka memahami cara model ini sebenarnya membuat keputusan, dan memastikan ketelusan dalam sistem AI, Amanah dan akauntabiliti untuk menyelesaikan masalah ini. Artikel ini meneroka pelbagai teknik kecerdasan buatan (XAI) yang boleh dijelaskan untuk menggambarkan prinsip asasnya. Beberapa sebab mengapa AI boleh dijelaskan adalah penting Kepercayaan dan ketelusan: Untuk sistem AI diterima secara meluas dan dipercayai, pengguna perlu memahami cara keputusan dibuat
 Lima sekolah pembelajaran mesin yang anda tidak tahu
Jun 05, 2024 pm 08:51 PM
Lima sekolah pembelajaran mesin yang anda tidak tahu
Jun 05, 2024 pm 08:51 PM
Pembelajaran mesin ialah cabang penting kecerdasan buatan yang memberikan komputer keupayaan untuk belajar daripada data dan meningkatkan keupayaan mereka tanpa diprogramkan secara eksplisit. Pembelajaran mesin mempunyai pelbagai aplikasi dalam pelbagai bidang, daripada pengecaman imej dan pemprosesan bahasa semula jadi kepada sistem pengesyoran dan pengesanan penipuan, dan ia mengubah cara hidup kita. Terdapat banyak kaedah dan teori yang berbeza dalam bidang pembelajaran mesin, antaranya lima kaedah yang paling berpengaruh dipanggil "Lima Sekolah Pembelajaran Mesin". Lima sekolah utama ialah sekolah simbolik, sekolah sambungan, sekolah evolusi, sekolah Bayesian dan sekolah analogi. 1. Simbolisme, juga dikenali sebagai simbolisme, menekankan penggunaan simbol untuk penaakulan logik dan ekspresi pengetahuan. Aliran pemikiran ini percaya bahawa pembelajaran adalah proses penolakan terbalik, melalui sedia ada
 Adakah Flash Attention stabil? Meta dan Harvard mendapati bahawa sisihan berat model mereka berubah-ubah mengikut urutan magnitud
May 30, 2024 pm 01:24 PM
Adakah Flash Attention stabil? Meta dan Harvard mendapati bahawa sisihan berat model mereka berubah-ubah mengikut urutan magnitud
May 30, 2024 pm 01:24 PM
MetaFAIR bekerjasama dengan Harvard untuk menyediakan rangka kerja penyelidikan baharu untuk mengoptimumkan bias data yang dijana apabila pembelajaran mesin berskala besar dilakukan. Adalah diketahui bahawa latihan model bahasa besar sering mengambil masa berbulan-bulan dan menggunakan ratusan atau bahkan ribuan GPU. Mengambil model LLaMA270B sebagai contoh, latihannya memerlukan sejumlah 1,720,320 jam GPU. Melatih model besar memberikan cabaran sistemik yang unik disebabkan oleh skala dan kerumitan beban kerja ini. Baru-baru ini, banyak institusi telah melaporkan ketidakstabilan dalam proses latihan apabila melatih model AI generatif SOTA Mereka biasanya muncul dalam bentuk lonjakan kerugian Contohnya, model PaLM Google mengalami sehingga 20 lonjakan kerugian semasa proses latihan. Bias berangka adalah punca ketidaktepatan latihan ini,




