Ringkasan mata pengetahuan penting yang berkaitan dengan model regresi pembelajaran mesin

​1. Apakah andaian regresi linear?

Regression linear mempunyai empat andaian:

• Linear: Perlu ada hubungan linear antara pembolehubah bebas (x) dan pembolehubah bersandar (y), yang bermaksud bahawa perubahan dalam nilai x juga harus mengubah nilai y ke arah yang sama.
• Kemerdekaan: Ciri harus bebas antara satu sama lain, yang bermaksud multikolineariti minimum.
• Kenormalan: Sisa hendaklah diagihkan secara normal.
• Homoskedastisitas: Varians titik data di sekeliling garis regresi hendaklah sama untuk semua nilai.

2. Apakah baki dan bagaimana ia digunakan untuk menilai model regresi?

Ralat baki merujuk kepada ralat antara nilai yang diramalkan dan nilai yang diperhatikan. Ia mengukur jarak titik data dari garis regresi. Ia dikira dengan menolak nilai ramalan daripada nilai yang diperhatikan.

Plot sisa ialah cara terbaik untuk menilai model regresi. Ia adalah graf yang menunjukkan semua baki pada paksi menegak dan ciri pada paksi-x. Jika titik data bertaburan secara rawak pada baris tanpa corak, maka model regresi linear sesuai dengan data dengan baik, jika tidak, kita harus menggunakan model bukan linear.

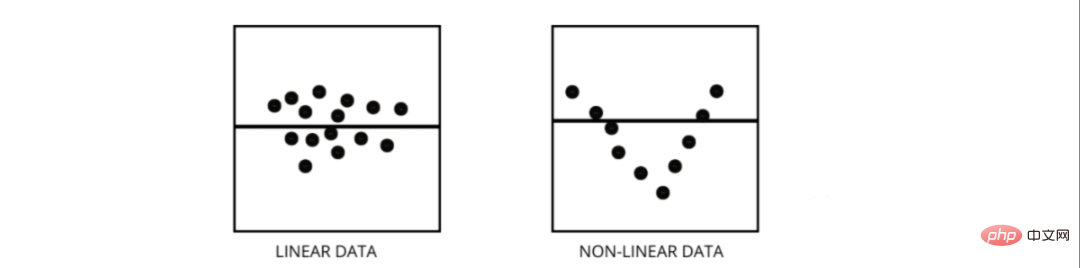
3. Bagaimana untuk membezakan antara model regresi linear dan model regresi bukan linear?

Kedua-duanya adalah jenis masalah regresi. Perbezaan antara kedua-duanya ialah data mereka dilatih.

Model regresi linear mengandaikan hubungan linear antara ciri dan label, yang bermaksud jika kita mengambil semua titik data dan memplotkannya ke dalam garisan linear (lurus) ia harus sesuai dengan data.

Model regresi bukan linear mengandaikan bahawa tiada hubungan linear antara pembolehubah. Garisan bukan linear (curvilinear) harus memisahkan dan sesuai dengan data dengan betul.

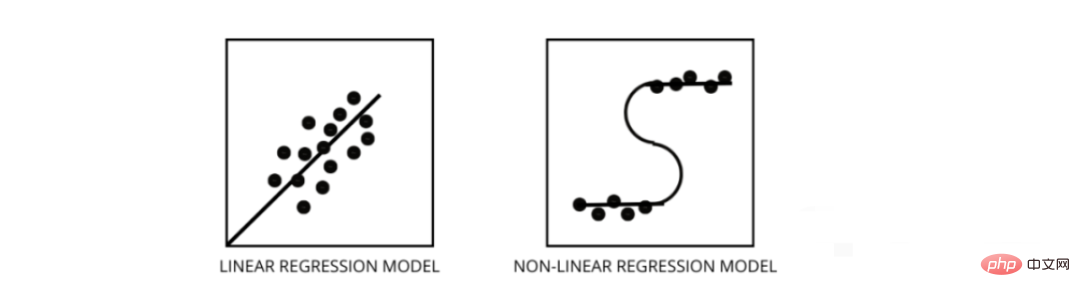
Tiga cara terbaik untuk mengetahui sama ada data anda adalah linear atau bukan linear -

1. Plot Baki
2. Angka Sebaran
3. Dengan mengandaikan data adalah linear, model linear dilatih dan dinilai mengikut ketepatan.

4. Apakah multikolineariti dan bagaimana ia mempengaruhi prestasi model?

Multikolineariti berlaku apabila ciri-ciri tertentu sangat berkorelasi antara satu sama lain. Korelasi merujuk kepada ukuran yang menunjukkan bagaimana satu pembolehubah dipengaruhi oleh perubahan dalam pembolehubah lain.

Jika peningkatan dalam ciri a membawa kepada peningkatan dalam ciri b, maka kedua-dua ciri tersebut berkorelasi secara positif. Jika peningkatan dalam a menyebabkan penurunan dalam ciri b, maka kedua-dua ciri tersebut berkorelasi negatif. Mempunyai dua pembolehubah yang sangat berkorelasi pada data latihan boleh membawa kepada multikolineariti kerana model itu tidak dapat mencari corak dalam data, mengakibatkan prestasi model yang lemah. Oleh itu, sebelum melatih model, kita mesti terlebih dahulu cuba menghapuskan multikolineariti.

5. Bagaimanakah outlier mempengaruhi prestasi model regresi linear?

Outlier ialah titik data yang nilainya berbeza daripada julat purata titik data. Dalam erti kata lain, mata ini berbeza daripada data atau di luar kriteria ke-3.

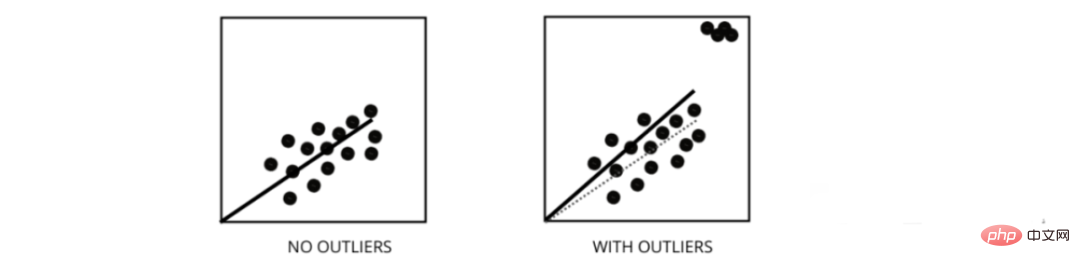
Model regresi linear cuba mencari garisan paling sesuai yang mengurangkan baki. Jika data mengandungi outlier, garisan paling sesuai akan beralih sedikit ke arah outlier, meningkatkan kadar ralat dan menghasilkan model dengan MSE yang sangat tinggi.

6. Apakah perbezaan antara MSE dan MAE?

MSE bermaksud ralat min kuasa dua, iaitu perbezaan kuasa dua antara nilai sebenar dan nilai ramalan. Dan MAE ialah perbezaan mutlak antara nilai sasaran dan nilai ramalan.

MSE menghukum kesilapan besar, MAE tidak. Apabila nilai MSE dan MAE berkurangan, model ini cenderung kepada garisan yang lebih sesuai.

7. Apakah regularisasi L1 dan L2 dan bilakah ia perlu digunakan?

Dalam pembelajaran mesin, matlamat utama kami adalah untuk mencipta model umum yang boleh berprestasi lebih baik pada data latihan dan ujian, tetapi apabila terdapat sangat sedikit data, model regresi linear asas cenderung untuk menyesuaikan diri, jadi kami akan menggunakan penyelarasan l1 dan l2.

Penyaturan L1 atau regresi laso menambah nilai mutlak cerun sebagai istilah penalti dalam fungsi kos. Membantu mengalih keluar outlier dengan mengalih keluar semua titik data dengan nilai cerun kurang daripada ambang.

Penyaturan L2 atau regresi rabung menambah tempoh penalti yang sama dengan kuasa dua saiz pekali. Ia menghukum ciri dengan nilai cerun yang lebih tinggi.

l1 dan l2 berguna apabila terdapat sedikit data latihan, varians yang tinggi, ciri yang diramalkan adalah lebih besar daripada nilai yang diperhatikan dan wujud multikolineariti dalam data.

8. Apakah maksud heteroskedastisitas?

Ia merujuk kepada situasi di mana varians titik data di sekeliling garisan paling sesuai tidak sama dalam julat. Ia mengakibatkan penyebaran sisa yang tidak sekata. Jika ia terdapat dalam data, maka model cenderung untuk meramalkan output tidak sah. Salah satu cara terbaik untuk menguji heteroskedastisitas adalah dengan memplot sisa.

Salah satu punca terbesar heteroskedastisitas dalam data ialah perbezaan besar antara ciri julat. Sebagai contoh, jika kita mempunyai lajur dari 1 hingga 100000, maka meningkatkan nilai sebanyak 10% tidak akan mengubah nilai yang lebih rendah, tetapi akan membuat perbezaan yang sangat besar pada nilai yang lebih tinggi, dengan itu menghasilkan perbezaan titik data yang besar .

9. Apakah peranan faktor inflasi varians?

Faktor inflasi varians (vif) digunakan untuk mengetahui sejauh mana pembolehubah bebas boleh diramal menggunakan pembolehubah bebas yang lain.

Mari kita ambil contoh data dengan ciri v1, v2, v3, v4, v5 dan v6. Sekarang, untuk mengira vif v1, pertimbangkan ia sebagai pembolehubah peramal dan cuba ramalkannya menggunakan semua pembolehubah peramal yang lain.

Jika nilai VIF adalah kecil, lebih baik untuk mengalih keluar pembolehubah daripada data. Kerana nilai yang lebih kecil menunjukkan korelasi yang tinggi antara pembolehubah.

10. Bagaimanakah regresi berperingkat berfungsi

Regresi berperingkat ialah kaedah mencipta model regresi dengan mengalih keluar atau menambah pembolehubah peramal dengan bantuan ujian hipotesis. Ia meramalkan pembolehubah bersandar dengan menguji secara berulang-ulang kepentingan setiap pembolehubah bebas dan mengalih keluar atau menambah beberapa ciri selepas setiap lelaran. Ia berjalan n kali dan cuba mencari gabungan terbaik parameter yang meramalkan pembolehubah bersandar dengan ralat terkecil antara nilai yang diperhatikan dan diramalkan.

Ia boleh mengurus sejumlah besar data dengan sangat cekap dan menyelesaikan masalah dimensi tinggi.

11 Sebagai tambahan kepada MSE dan MAE, adakah terdapat petunjuk regresi penting lain?

Kami menggunakan masalah regresi untuk memperkenalkan penunjuk ini, di mana input kami adalah pengalaman kerja dan output adalah gaji. Graf di bawah menunjukkan garis regresi linear yang dilukis untuk meramalkan gaji.

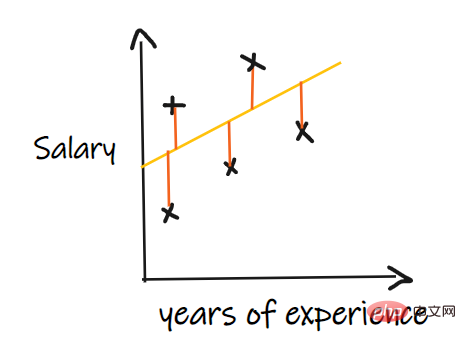
1 Min ralat mutlak (MAE):

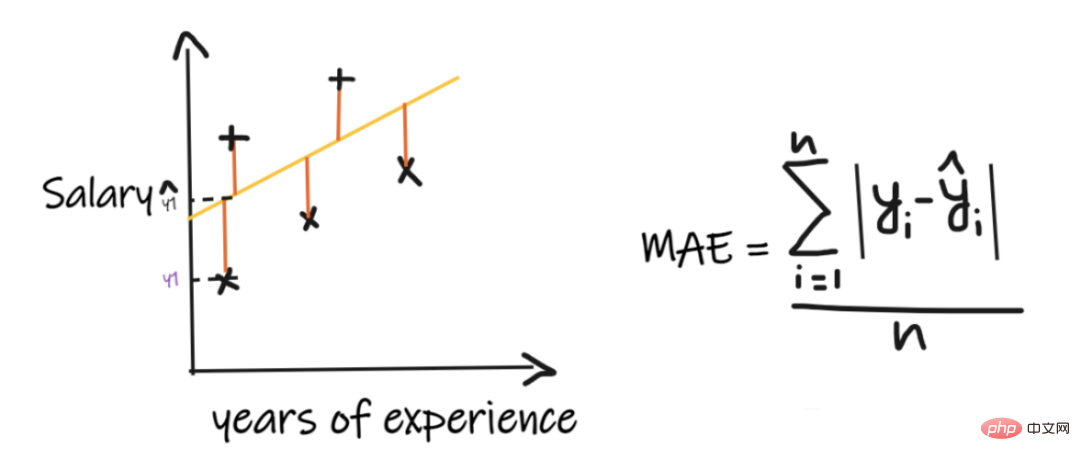
Min ralat mutlak (MAE) ialah ukuran regresi yang paling mudah. . Ia menambah perbezaan antara setiap nilai sebenar dan ramalan dan membahagikannya dengan bilangan pemerhatian. Untuk model regresi dianggap sebagai model yang baik, MAE hendaklah sekecil mungkin.

Kelebihan MAE ialah:

Mudah dan mudah difahami. Hasilnya akan mempunyai unit yang sama dengan output. Sebagai contoh: Jika unit lajur output ialah LPA, maka jika MAE ialah 1.2, maka kita boleh mentafsirkan hasilnya sebagai +1.2LPA atau -1.2LPA, MAE secara relatifnya stabil kepada outlier (berbanding dengan beberapa penunjuk regresi lain, MAE dipengaruhi oleh kesan terpencil kurang).

Kelemahan MAE ialah:

MAE menggunakan fungsi modular, tetapi fungsi modular tidak boleh dibezakan pada semua titik, jadi ia tidak boleh digunakan sebagai fungsi kehilangan dalam banyak kes.

2. Ralat min kuasa dua (MSE):

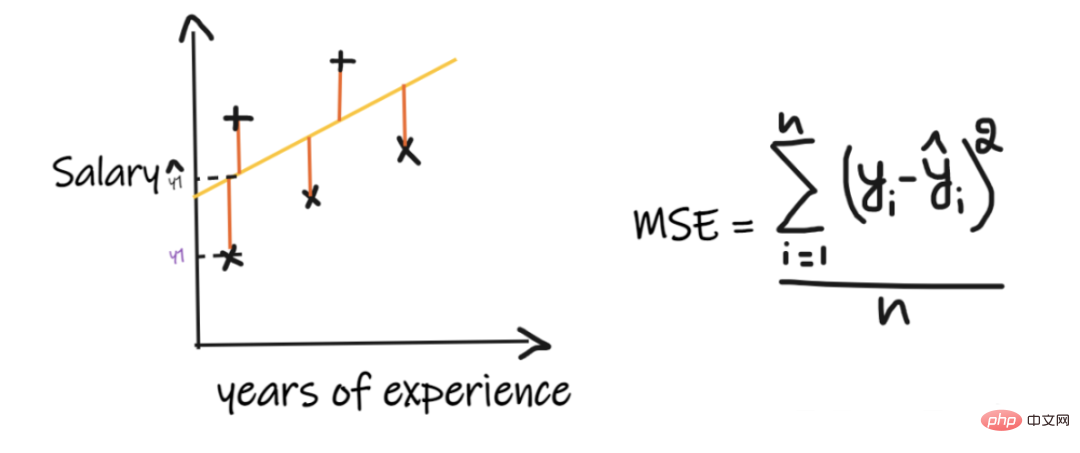
MSE mengambil perbezaan antara setiap nilai sebenar dan nilai ramalan, kemudian kuasa duakan perbezaan dan menambahnya bersama-sama, akhirnya membahagikan dengan bilangan pemerhatian. Untuk model regresi dianggap sebagai model yang baik, MSE hendaklah sekecil mungkin.

Kelebihan MSE: Fungsi segi empat sama boleh dibezakan di semua titik, jadi ia boleh digunakan sebagai fungsi kehilangan.

Kelemahan MSE: Memandangkan MSE menggunakan fungsi segi empat sama, unit hasilnya ialah kuasa dua keluaran. Oleh itu, sukar untuk mentafsir keputusan. Memandangkan ia menggunakan fungsi segi empat sama, jika terdapat outlier dalam data, perbezaan juga akan menjadi kuasa dua, dan oleh itu, MSE tidak stabil untuk outlier.

3. Ralat purata kuasa dua akar (RMSE):

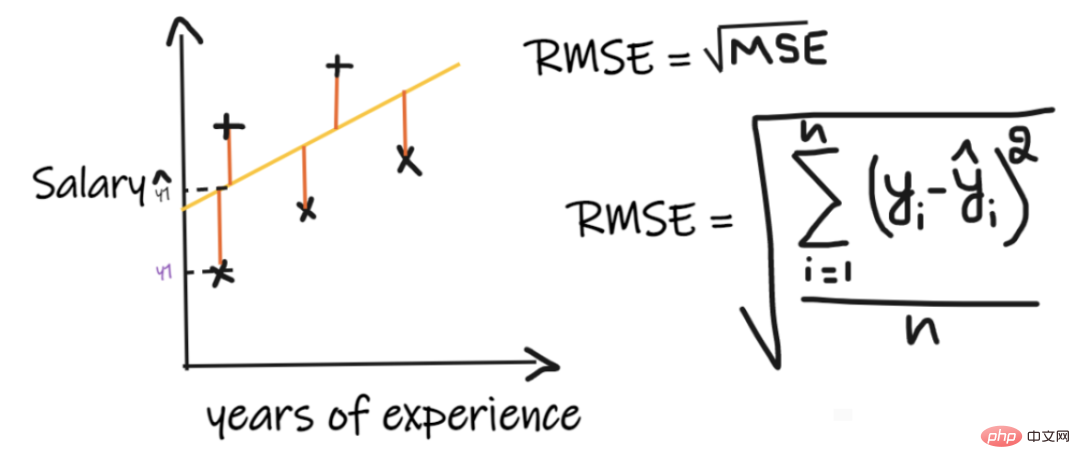
Ralat purata kuasa dua akar (RMSE) mengambil perbezaan antara setiap nilai sebenar dan nilai ramalan nilai, kemudian kuasa duakan perbezaan dan tambahkannya, dan akhirnya bahagikan dengan bilangan pemerhatian. Kemudian ambil punca kuasa dua hasilnya. Oleh itu, RMSE ialah punca kuasa dua MSE. Untuk model regresi dianggap sebagai model yang baik, RMSE hendaklah sekecil mungkin.

RMSE menyelesaikan masalah MSE, unit akan sama dengan output kerana ia mengambil punca kuasa dua, tetapi masih kurang stabil kepada outlier.

Penunjuk di atas bergantung pada konteks masalah yang kita selesaikan Kita tidak boleh menilai kualiti model dengan hanya melihat nilai MAE, MSE dan RMSE tanpa memahami masalah sebenar.

4. Skor R2:

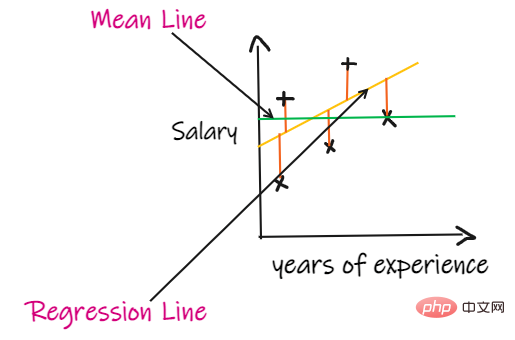
Jika kita tiada data input, tetapi ingin tahu berapa gaji yang dia boleh dapat dalam syarikat ini, maka kita boleh Perkara terbaik untuk dilakukan ialah memberi mereka purata semua gaji pekerja.

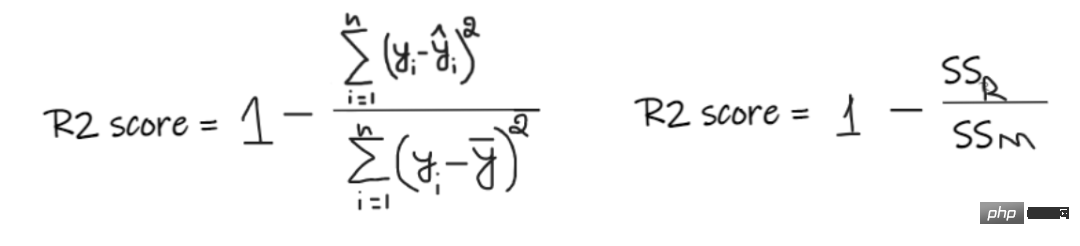
Skor R2 memberikan nilai antara 0 dan 1 dan boleh ditafsirkan untuk sebarang konteks. Ia boleh difahami sebagai kualiti kesesuaian.

SSR ialah jumlah ralat kuasa dua bagi garis regresi, dan SSM ialah jumlah ralat kuasa dua bagi purata bergerak. Kami membandingkan garis regresi dengan garis min.

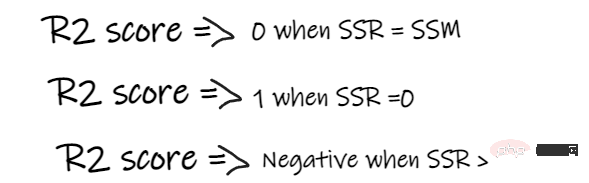
• Jika skor R2 ialah 0, bermakna model kami mempunyai hasil yang sama dengan purata, jadi model kami perlu diperbaiki.
• Jika skor R2 ialah 1, bahagian kanan persamaan menjadi 0, yang hanya boleh berlaku jika model kami sesuai dengan setiap titik data tanpa ralat.
• Jika skor R2 negatif, ini bermakna bahagian kanan persamaan lebih besar daripada 1, yang boleh berlaku apabila SSR > SSM. Ini bermakna model kami adalah paling teruk daripada purata, bermakna model kami lebih teruk daripada mengambil purata untuk meramalkan

Jika skor R2 model kami ialah 0.8, ini bermakna ia boleh dikatakan bahawa model boleh Menerangkan 80% varians keluaran. Iaitu, 80% daripada variasi gaji boleh dijelaskan oleh input (tahun bekerja), tetapi baki 20% tidak diketahui.

Jika model kami mempunyai 2 ciri, tahun bekerja dan markah temu duga, maka model kami boleh menerangkan 80% daripada perubahan gaji menggunakan dua ciri input ini.

Kelemahan R2:

Apabila bilangan ciri input meningkat, R2 akan cenderung meningkat dengan sewajarnya atau kekal sama, tetapi tidak akan berkurangan, walaupun ciri input tidak berguna untuk kita model penting (cth., menambahkan suhu pada hari temu duga kepada contoh kami, R2 tidak akan berkurangan walaupun suhu tidak penting kepada output).

5. Markah R2 terlaras:

Dalam formula di atas, R2 ialah R2, n ialah bilangan cerapan (baris), dan p ialah bilangan ciri bebas. R2 terlaras menyelesaikan masalah R2.

Apabila kami menambah ciri yang kurang penting untuk model kami, seperti menambah suhu untuk meramalkan gaji.....

Apabila menambah ciri yang penting kepada model, seperti menambah markah temu duga untuk meramal gaji...

Perkara di atas ialah masalah regresi Mata pengetahuan penting dan pengenalan pelbagai petunjuk penting yang digunakan untuk menyelesaikan masalah regresi serta kelebihan dan kekurangannya, saya harap ia akan membantu anda.

Atas ialah kandungan terperinci Ringkasan mata pengetahuan penting yang berkaitan dengan model regresi pembelajaran mesin. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!