
Kertas kerja ini adalah tentang kerja pembelajaran peneguhan mendalam untuk menentang serangan. Dalam makalah ini, penulis mengkaji keteguhan strategi pembelajaran peneguhan mendalam kepada serangan musuh dari perspektif pengoptimuman yang mantap. Di bawah rangka kerja pengoptimuman yang teguh, serangan musuh yang optimum diberikan dengan meminimumkan pulangan jangkaan strategi, dan sewajarnya, mekanisme pertahanan yang baik dicapai dengan meningkatkan prestasi strategi dalam menghadapi senario kes terburuk.
Memandangkan penyerang biasanya tidak dapat menyerang dalam persekitaran latihan, penulis mencadangkan algoritma serangan tamak yang cuba meminimumkan pulangan strategi yang dijangkakan tanpa berinteraksi dengan persekitaran di samping itu, penulis juga mencadangkan a Algoritma pertahanan yang menggunakan permainan max-min untuk menjalankan latihan menentang algoritma pembelajaran pengukuhan mendalam.
Hasil percubaan dalam persekitaran permainan Atari menunjukkan bahawa algoritma serangan lawan yang dicadangkan oleh pengarang adalah lebih berkesan daripada algoritma serangan sedia ada, dan kadar pulangan strategi adalah lebih teruk. Strategi yang dijana oleh algoritma pertahanan lawan yang dicadangkan dalam kertas kerja adalah lebih teguh kepada pelbagai serangan lawan daripada kaedah pertahanan sedia ada.
Memandangkan sebarang sampel (x, y) dan rangkaian saraf f, matlamat pengoptimuman untuk menghasilkan sampel lawan ialah:
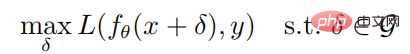
di manakah parameter rangkaian saraf f, L ialah fungsi kehilangan, ialah set gangguan musuh,  ialah bola terkekang norma dengan x sebagai pusat dan jejari sebagai jejari. Formula pengiraan untuk menjana sampel lawan melalui serangan PGD adalah seperti berikut:
ialah bola terkekang norma dengan x sebagai pusat dan jejari sebagai jejari. Formula pengiraan untuk menjana sampel lawan melalui serangan PGD adalah seperti berikut:
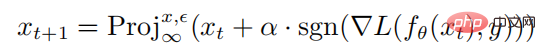
di mana  mewakili operasi unjuran jika input berada di luar sfera norma, input akan diunjurkan Pada sfera dengan pusat x dan sebagai jejari, mewakili saiz gangguan satu langkah serangan PGD.
mewakili operasi unjuran jika input berada di luar sfera norma, input akan diunjurkan Pada sfera dengan pusat x dan sebagai jejari, mewakili saiz gangguan satu langkah serangan PGD.
2.2 Pembelajaran Pengukuhan dan Kecerunan Dasar
Masalah pembelajaran pengukuhan boleh digambarkan sebagai proses keputusan Markov. Proses keputusan Markov boleh ditakrifkan sebagai lima kali ganda 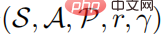 , di mana S mewakili ruang keadaan, A mewakili ruang tindakan,
, di mana S mewakili ruang keadaan, A mewakili ruang tindakan, 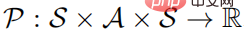 mewakili kebarangkalian peralihan keadaan, dan r mewakili Fungsi ganjaran mewakili faktor diskaun. Matlamat pembelajaran pembelajaran yang kukuh adalah untuk mempelajari taburan dasar parameter
mewakili kebarangkalian peralihan keadaan, dan r mewakili Fungsi ganjaran mewakili faktor diskaun. Matlamat pembelajaran pembelajaran yang kukuh adalah untuk mempelajari taburan dasar parameter  untuk memaksimumkan fungsi nilai
untuk memaksimumkan fungsi nilai
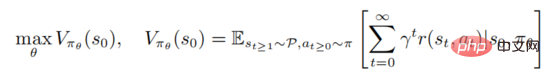
di mana mewakili keadaan awal. Pembelajaran kukuh melibatkan penilaian fungsi nilai tindakan
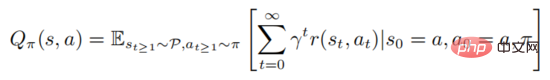
Formula di atas menerangkan jangkaan matematik untuk mematuhi dasar selepas negara dilaksanakan. Ia boleh dilihat daripada definisi bahawa fungsi nilai dan fungsi nilai tindakan memenuhi perhubungan berikut:
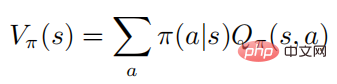
Untuk kemudahan ekspresi, penulis memberi tumpuan terutamanya pada proses Markov ruang tindakan diskret, tetapi semua algoritma dan keputusan boleh digunakan terus pada tetapan berturut-turut.
Serangan lawan dan pertahanan strategi pembelajaran pengukuhan mendalam adalah berdasarkan rangka kerja PGD pengoptimuman teguh
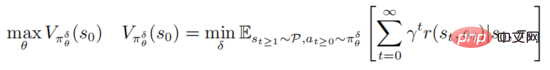
di mana mewakili  , mewakili set urutan gangguan musuh
, mewakili set urutan gangguan musuh  , dan untuk semua
, dan untuk semua 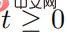 , memuaskan
, memuaskan 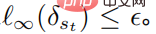 Formula di atas menyediakan rangka kerja bersatu untuk pembelajaran peneguhan mendalam untuk memerangi serangan dan pertahanan.
Formula di atas menyediakan rangka kerja bersatu untuk pembelajaran peneguhan mendalam untuk memerangi serangan dan pertahanan.
Di satu pihak, pengoptimuman pengecilan dalaman berusaha untuk mencari urutan gangguan musuh yang menjadikan strategi semasa membuat keputusan yang salah. Sebaliknya, tujuan pemaksiman luaran adalah untuk mencari parameter pengedaran strategi untuk memaksimumkan pulangan yang dijangkakan di bawah strategi gangguan. Selepas serangan lawan dan permainan pertahanan di atas, parameter strategi semasa proses latihan akan lebih tahan terhadap serangan lawan.
Tujuan meminimumkan dalaman fungsi objektif adalah untuk menjana gangguan musuh, tetapi untuk algoritma pembelajaran pengukuhan untuk mempelajari gangguan musuh yang optimum adalah sangat memakan masa dan intensif buruh, dan kerana persekitaran latihan adalah Ia adalah kotak hitam, jadi dalam kertas ini, penulis mempertimbangkan tetapan praktikal, iaitu, penyerang menyuntik gangguan di negeri yang berbeza. Dalam senario serangan pembelajaran yang diselia, penyerang hanya perlu menipu model pengelas untuk menjadikannya salah klasifikasi dan menghasilkan label yang salah dalam senario serangan pembelajaran pengukuhan, fungsi nilai tindakan menyediakan penyerang dengan maklumat tambahan, iaitu nilai tingkah laku yang kecil; akan Menghasilkan pulangan jangkaan yang kecil. Sejajar dengan itu, pengarang mentakrifkan gangguan musuh yang optimum dalam pembelajaran peneguhan mendalam seperti berikut
Definisi 1: Gangguan musuh yang optimum pada keadaan dapat meminimumkan pulangan yang dijangkakan negeri
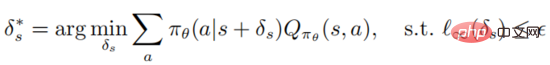
Perlu diambil perhatian bahawa mengoptimumkan dan menyelesaikan formula di atas adalah sangat rumit Ia perlu memastikan bahawa penyerang boleh memperdaya ejen untuk memilih tingkah laku membuat keputusan yang paling teruk Walau bagaimanapun, bagi penyerang, nilai tindakan ejen fungsi adalah agnostik, jadi tidak ada jaminan bahawa ia akan optimum terhadap gangguan. Teorem berikut boleh menunjukkan bahawa jika dasar adalah optimum, gangguan musuh yang optimum boleh dijana tanpa mengakses fungsi nilai tindakan
Teorem 1: Apabila strategi kawalan 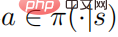 adalah optimum, nilai tindakan Fungsi dan strategi memenuhi perhubungan berikut
adalah optimum, nilai tindakan Fungsi dan strategi memenuhi perhubungan berikut
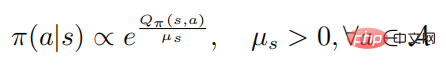
di mana mewakili entropi dasar, adalah pemalar bergantung kepada keadaan, dan apabila berubah kepada 0, ia juga akan berubah kepada 0, Tambahan pula, perkara berikut formula
membuktikan: Apabila strategi rawak 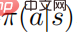 mencapai optimum, fungsi nilai
mencapai optimum, fungsi nilai 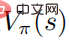 juga mencapai optimum, yang bermaksud bahawa dalam setiap keadaan, adalah mustahil untuk mencari mana-mana taburan tingkah laku lain seperti bahawa fungsi nilai
juga mencapai optimum, yang bermaksud bahawa dalam setiap keadaan, adalah mustahil untuk mencari mana-mana taburan tingkah laku lain seperti bahawa fungsi nilai 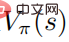 meningkat. Sejajar dengan itu, memandangkan fungsi nilai tindakan optimum
meningkat. Sejajar dengan itu, memandangkan fungsi nilai tindakan optimum 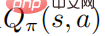 , strategi optimum
, strategi optimum 
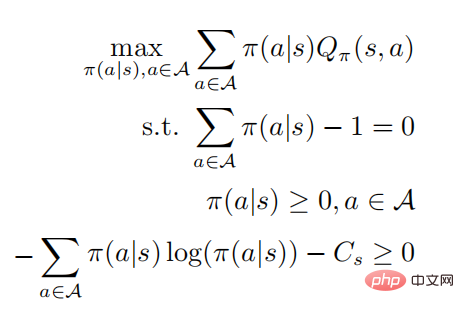
boleh diperolehi dengan menyelesaikan masalah pengoptimuman terkurung taburan kebarangkalian, dan baris terakhir mewakili bahawa strategi adalah strategi rawak Mengikut keadaan KKT, masalah pengoptimuman di atas boleh diubah menjadi bentuk berikut:
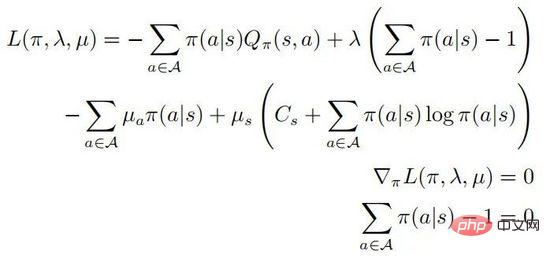
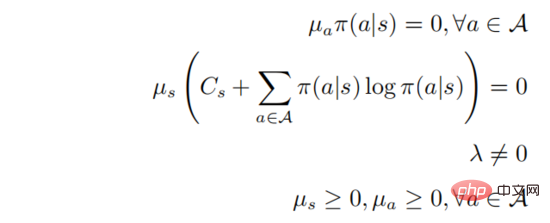
yang mana 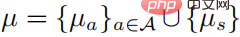 . Anggap bahawa
. Anggap bahawa 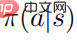 adalah pasti positif untuk semua tindakan
adalah pasti positif untuk semua tindakan 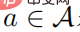 , maka:
, maka:
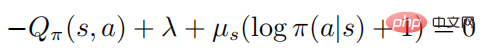
Apabila 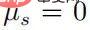 , maka mesti ada
, maka mesti ada 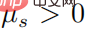 , dan kemudian untuk mana-mana
, dan kemudian untuk mana-mana 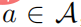 , maka terdapat
, maka terdapat 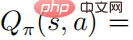 , dengan itu hubungan softmax antara fungsi nilai tindakan dan strategi akan diperoleh
, dengan itu hubungan softmax antara fungsi nilai tindakan dan strategi akan diperoleh
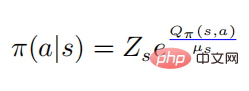
di mana  , maka terdapat
, maka terdapat
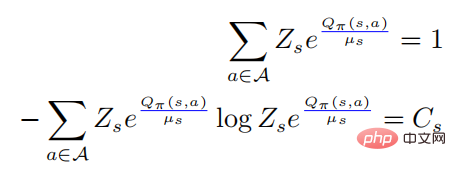
Membawa persamaan pertama di atas ke dalam persamaan kedua, kita mempunyai
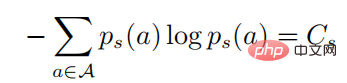
antaranya
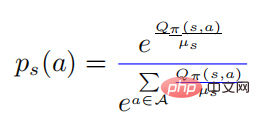
Dalam formula di atas, 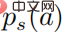 mewakili taburan kebarangkalian dalam bentuk softmax, dan entropinya adalah sama dengan . Apabila bersamaan dengan 0, juga menjadi 0. Dalam kes ini, adalah lebih besar daripada 0, maka
mewakili taburan kebarangkalian dalam bentuk softmax, dan entropinya adalah sama dengan . Apabila bersamaan dengan 0, juga menjadi 0. Dalam kes ini, adalah lebih besar daripada 0, maka  pada masa ini.
pada masa ini.
Teorem 1 menunjukkan bahawa jika polisi adalah optimum, gangguan optimum boleh diperolehi dengan memaksimumkan entropi silang polisi bermasalah dan polisi asal. Untuk kesederhanaan perbincangan, penulis memanggil serangan Teorem 1 sebagai serangan strategik, dan penulis menggunakan rangka kerja algoritma PGD untuk mengira serangan strategik yang optimum Carta aliran algoritma khusus ditunjukkan dalam Algoritma 1 di bawah.

Carta alir algoritma pengoptimuman teguh untuk pertahanan terhadap gangguan yang dicadangkan oleh pengarang ditunjukkan dalam Algoritma 2 di bawah. Algoritma ini dipanggil latihan lawan serangan strategik. Semasa fasa latihan, dasar gangguan digunakan untuk berinteraksi dengan persekitaran, dan pada masa yang sama fungsi nilai tindakan 〈🎜〉 dasar gangguan dianggarkan membantu latihan dasar. 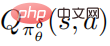
Sukar untuk dikendalikan kerana trajektori dikumpul dengan menjalankan dasar yang terganggu, dan menggunakan data ini untuk menganggarkan fungsi nilai tindakan bagi dasar yang tidak terganggu boleh menjadi sangat Tidak tepat. 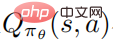

Fungsi objektif strategi gangguan yang dioptimumkan 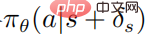 menggunakan PPO ialah
menggunakan PPO ialah
dengan 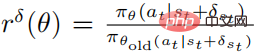 , dan
, dan 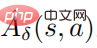 ialah anggaran fungsi purata strategi gangguan
ialah anggaran fungsi purata strategi gangguan 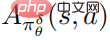 . Dalam amalan,
. Dalam amalan, 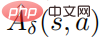 dianggarkan dengan kaedah GAE. Carta aliran algoritma khusus ditunjukkan dalam rajah di bawah.
dianggarkan dengan kaedah GAE. Carta aliran algoritma khusus ditunjukkan dalam rajah di bawah.

Tiga sub-angka di sebelah kanan di bawah menunjukkan hasil gangguan serangan yang berbeza. Ia boleh didapati bahawa kedua-dua dasar terlatih songsang dan dasar standard adalah tahan terhadap gangguan rawak. Sebaliknya, serangan musuh merendahkan prestasi strategi yang berbeza. Hasilnya bergantung pada persekitaran ujian dan algoritma pertahanan, dan selanjutnya ia boleh didapati bahawa jurang prestasi antara tiga algoritma serangan musuh adalah kecil.
Sebaliknya, dalam tetapan yang agak sukar, strategi yang dicadangkan oleh pengarang kertas kerja untuk menyerang gangguan algoritma menghasilkan pulangan yang jauh lebih rendah. Secara keseluruhan, algoritma serangan strategik yang dicadangkan dalam kertas kerja menghasilkan ganjaran terendah dalam kebanyakan kes, menunjukkan bahawa ia sememangnya yang paling cekap daripada semua algoritma serangan musuh yang diuji.

Seperti yang ditunjukkan dalam rajah di bawah, lengkung pembelajaran algoritma pertahanan yang berbeza dan PPO standard ditunjukkan. Adalah penting untuk ambil perhatian bahawa keluk prestasi hanya mewakili jangkaan pulangan strategi yang digunakan untuk berinteraksi dengan persekitaran. Di antara semua algoritma latihan, ATPA yang dicadangkan dalam kertas kerja mempunyai varians latihan yang paling rendah dan oleh itu lebih stabil daripada algoritma lain. Juga perhatikan bahawa ATPA berkembang jauh lebih perlahan daripada PPO standard, terutamanya dalam peringkat latihan awal. Ini membawa kepada fakta bahawa pada peringkat awal latihan, diganggu oleh faktor-faktor yang merugikan boleh menjadikan latihan dasar sangat tidak stabil. Jadual
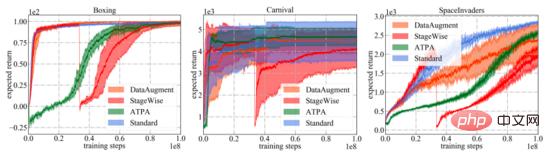
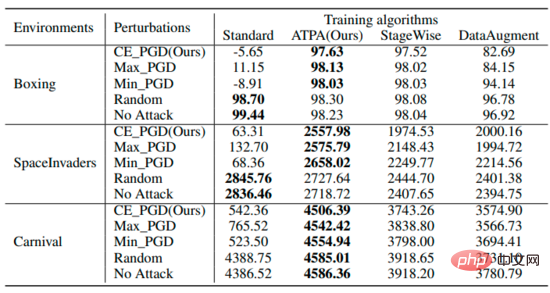
meringkaskan jangkaan pulangan strategi di bawah gangguan berbeza menggunakan algoritma berbeza. Ia boleh didapati bahawa strategi terlatih ATPA tahan terhadap pelbagai gangguan musuh. Sebagai perbandingan, walaupun StageWise dan DataAugment telah belajar untuk mengendalikan serangan musuh sedikit sebanyak, ia tidak berkesan seperti ATPA dalam semua kes.
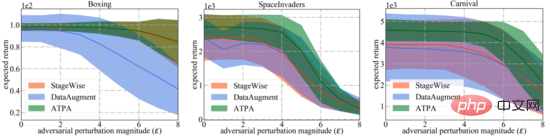
Untuk perbandingan yang lebih luas, penulis juga menilai keteguhan algoritma pertahanan ini kepada pelbagai peringkat gangguan yang dihasilkan oleh algoritma serangan strategik yang paling berkesan. Seperti yang ditunjukkan di bawah, ATPA sekali lagi menerima markah tertinggi dalam semua kes. Di samping itu, varians penilaian ATPA jauh lebih kecil daripada StageWise dan DataAugment, menunjukkan bahawa ATPA mempunyai keupayaan generatif yang lebih kuat.
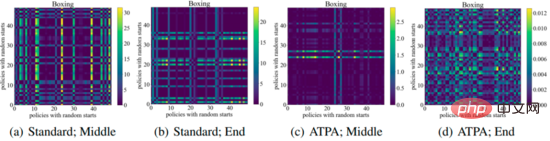
Untuk mencapai prestasi yang serupa, ATPA memerlukan lebih banyak data latihan daripada algoritma PPO standard. Penulis mendalami isu ini dengan mengkaji kestabilan strategi gangguan. Penulis mengira nilai perbezaan KL bagi polisi bermasalah yang diperoleh dengan melakukan serangan polisi menggunakan PGD dengan titik awal rawak yang berbeza di tengah dan pada akhir proses latihan. Seperti yang ditunjukkan dalam rajah di bawah, tanpa latihan lawan, nilai perbezaan KL yang besar diperhatikan secara berterusan walaupun PPO standard telah menumpu, menunjukkan bahawa dasar itu sangat tidak stabil terhadap gangguan yang dihasilkan oleh melaksanakan PGD dengan titik permulaan yang berbeza.
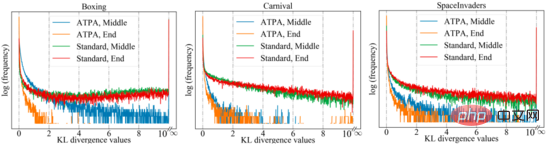
Rajah berikut menunjukkan plot divergence KL bagi strategi gangguan dengan titik awal yang berbeza Ia boleh didapati bahawa setiap piksel dalam rajah mewakili nilai divergence KL bagi kedua-duanya strategi gangguan , kedua-dua strategi gangguan ini diberikan dengan memaksimumkan formula teras algoritma ATPA. Ambil perhatian bahawa memandangkan perbezaan KL ialah metrik tidak simetri, pemetaan ini juga tidak simetri.
Atas ialah kandungan terperinci Serangan dan pertahanan musuh dalam pembelajaran peneguhan mendalam. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
 Bagaimana untuk membuka fail mobi
Bagaimana untuk membuka fail mobi
 Bagaimana untuk memulihkan fail yang dikosongkan daripada Recycle Bin
Bagaimana untuk memulihkan fail yang dikosongkan daripada Recycle Bin
 Bolehkah pemacu c dikembangkan?
Bolehkah pemacu c dikembangkan?
 Pengenalan kepada kaedah pelaksanaan kesan khas Java
Pengenalan kepada kaedah pelaksanaan kesan khas Java
 Bagaimana menggunakan beribu-ribu untuk membuat ratusan ribu dalam bulatan mata wang
Bagaimana menggunakan beribu-ribu untuk membuat ratusan ribu dalam bulatan mata wang
 Cara menggunakan makro excel
Cara menggunakan makro excel
 Terdapat beberapa fungsi output dan input dalam bahasa C
Terdapat beberapa fungsi output dan input dalam bahasa C
 Ciri-ciri rangkaian komputer yang paling menonjol
Ciri-ciri rangkaian komputer yang paling menonjol




