Bagaimana untuk membuktikan bahawa masalah adalah masalah VPN? Para saintis komputer telah menemui cara yang mudah

Masalah P/NP adalah masalah yang tidak dapat diselesaikan dalam bidang kerumitan pengiraan. Orang ramai telah cuba mencari jawapan kepada soalan: "Bolehkah kita menyelesaikan semua masalah pengkomputeran dengan cekap dalam masa yang munasabah

Apakah masa yang munasabah? Malah, masalah yang boleh diselesaikan sebelum akhir alam semesta dianggap dalam masa yang munasabah. Namun banyak masalah kelihatan sukar untuk diselesaikan dalam masa yang munasabah, memerlukan matematik untuk menunjukkan kesukaran masalah ini.

Kajian 2021 menjawab soalan di atas, yang mengesahkan: Sebilangan besar masalah sukar diselesaikan dengan berkesan.

Paul Beame dari University of Washington mengulas mengenai penyelidikan ini: "Sama seperti mendaki gunung, penyelidikan ini adalah pijakan di jalan menuju penyelidikan teori pengiraan." >

Tiga penyelidik kajian: saintis komputer Srikanth Srinivasan (kiri), Nutan Limaye (kanan atas) dan Sébastien Tavenas.

Kajian ini menganggap masalah yang melibatkan hanya penambahan dan pendaraban, tetapi ia menjadi sangat sukar apabila masalah ini terhad kepada penyelesaian dengan cara tertentu (pola selang seli penambahan dan pendaraban). Anehnya, kajian itu tidak menggunakan rangka kerja atau alat baharu, sebaliknya, pengarang berjaya memintas kerjasama selama beberapa dekad antara Wigderson, seorang profesor di Sekolah Matematik di Institut Kajian Lanjutan di Princeton, dan Noam Nisan dari Hebrew University of Jerusalem halangan yang diterangkan dalam karya itu.

Salah seorang penyelidik, Srikanth Srinivasan dari Universiti Aarhus di Denmark, berkata: "Kami menyedari bahawa terdapat cara yang sangat mudah untuk mengatasi halangan ini. Dan jika kami boleh melakukannya dengan cara yang begitu mudah, kami Jika anda fikir sesuatu adalah mustahil, anda pasti boleh mencari cara yang lebih baik 》

Soalan Penting

Selepas kemunculan komputer, saintis telah mendapati bahawa algoritma komputer boleh menyelesaikan banyak masalah, tetapi kadangkala ini. kos algoritma terlalu banyak mengambil masa terlalu lama - lebih lama daripada masa pengiraan sebenar.

Mereka mula mengesyaki bahawa sesetengah masalah sememangnya terlalu sukar untuk diselesaikan, tidak kira betapa besar atau kecilnya. Sebagai contoh, dalam graf, masalah penting adalah untuk menentukan sama ada terdapat laluan Hamiltonian, iaitu, terdapat laluan yang melalui setiap bucu tepat sekali. Meningkatkan bilangan bucu (dan tepi) harus mengambil masa yang lebih lama untuk menentukan sama ada laluan sedemikian wujud, tetapi algoritma terbaik pun mengambil masa yang lebih lama secara eksponen apabila saiz graf meningkat, menjadikan penyelesaian ini Masalahnya menjadi tidak realistik.

Saintis komputer cuba membuktikan bahawa mana-mana algoritma yang berkesan dalam beberapa cara untuk menyelesaikan satu masalah sukar dalam kelas masalah tertentu boleh diterjemahkan kepada penyelesaian kepada masalah lain yang serupa. masalah. Mereka memanggil jenis masalah ini sebagai masalah NP.

Sudah tentu, terdapat banyak masalah yang kelihatan tidak sukar dan tidak mengambil terlalu banyak masa untuk diselesaikan. Banyak daripada masalah ini juga setara dalam erti kata tertentu, dan masalah tersebut dipanggil masalah P. Mereka berpendapat bahawa masalah NP sememangnya lebih sukar daripada masalah P dan masalah NP tidak boleh diselesaikan dengan cekap. Tetapi tanpa bukti, idea ini mungkin salah.

Jadi saintis komputer mula mencari cara untuk membuktikan bahawa masalah NP sememangnya lebih sukar. Ini memerlukan menunjukkan bahawa masalah NP mesti mengambil masa eksponen untuk diselesaikan, tetapi membuktikan ini bukan mudah.

Seberapa sukar "keras"?

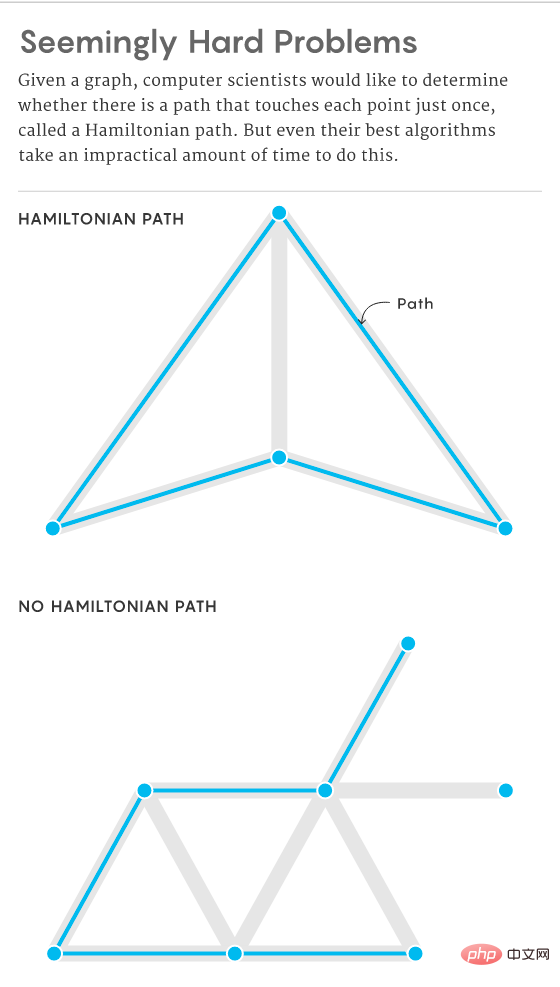
Bayangkan satu set masalah khusus yang hanya memerlukan penambahan dan pendaraban. Sebagai contoh, diberikan satu set mata, adalah mungkin untuk mengira semua laluan Hamiltonian yang mungkin (jika wujud) menggunakan data tentang titik, hanya dengan penambahan dan pendaraban.

Apabila saiz masalah bertambah, beberapa masalah aritmetik (seperti mengira laluan Hamiltonian) mengambil lebih masa. Pada tahun 1979, Leslie Valiant dari Universiti Harvard menunjukkan bahawa banyak masalah aritmetik adalah setara dari segi kesukaran, manakala yang lain adalah setara dari segi tiada kesukaran. Para saintis komputer kemudiannya menamakan kedua-dua jenis masalah ini-VNP dan VP, masing-masing-selepas dia.

Seperti masalah P dan NP, kami tidak dapat membuktikan kesukaran masalah VNP Kami hanya tahu bahawa masalah VNP lebih sukar daripada masalah NP kerana ia berdasarkan kepada yang terakhir laluan, anda perlu terlebih dahulu menentukan laluan wujud.

"Ia lebih sukar daripada NP, jadi lebih mudah untuk menunjukkan bahawa ia sukar," kata Shpilka.

Dalam dekad berikutnya, saintis komputer telah mencapai kemajuan yang lebih besar dalam masalah VP vs. VNP berbanding masalah P vs. NP, tetapi kebanyakannya terhad kepada apa yang dicipta oleh Valiant yang dipanggil subbidang kerumitan algebra. Sebelum kerja Limaye, Srinivasan, dan Tavenas baru-baru ini, masih sukar untuk mengetahui sama ada terdapat masalah dengan aritmetik dalam erti kata umum.

Melaraskan Polinomial

Kerja baharu ini membantu meneroka cara saintis komputer berfikir tentang masalah penambahan dan pendaraban. Secara matematik, masalah ini boleh ditulis dalam bentuk polinomial (cth. x^2 + 5y + 6) yang terdiri daripada pembolehubah yang ditambah dan didarab.

Untuk sebarang masalah tertentu, seperti mengira laluan Hamiltonian, anda boleh membina polinomial yang mewakilinya. Contohnya anda boleh menggunakan pembolehubah untuk mewakili setiap titik dan tepi, supaya apabila lebih banyak titik dan tepi ditambah, lebih banyak pembolehubah boleh ditambah pada polinomial.

Untuk menunjukkan bahawa masalah aritmetik seperti mengira laluan Hamiltonian adalah sukar, seseorang perlu menunjukkan bahawa apabila lebih banyak titik dan tepi ditambah, polinomial yang sepadan memerlukan lebih banyak operasi untuk diselesaikan dalam masa eksponen. Sebagai contoh, x^2 memerlukan satu operasi (x * x), manakala x^2 + y memerlukan dua operasi (x * x tambah y). Bilangan operasi dipanggil saiz polinomial.

Tetapi saiz polinomial sukar ditentukan. Contohnya polinomial x^2 + 2x + 1. Nampaknya mempunyai saiz 4 (dua pendaraban dan dua penambahan), tetapi polinomial boleh ditulis semula sebagai hasil darab dua jumlah, (x + 1)(x + 1), yang mempunyai lebih sedikit operan - dua kali Penambahan, satu pendaraban. Selalunya, apabila masalah bertambah dalam saiz dan lebih banyak pembolehubah ditambah pada polinomial, transformasi matematik boleh membantu memudahkan dan mengurangkan saiznya.

Beberapa tahun selepas penyelidikan Valiant, saintis komputer menemui cara untuk menjadikan saiz masalah lebih mudah untuk dianalisis. Untuk melakukan ini, mereka mencadangkan sifat yang dipanggil kedalaman, yang menentukan bilangan kali polinomial bertukar atau bergantian antara jumlah dan hasil. Contohnya, polinomial x^2 + 2x + 1 mempunyai kedalaman 2 kerana ia adalah hasil tambah (seperti x^2 dan 2x). Sebaliknya, ungkapan (x + 1)(x + 1) mempunyai kedalaman 3 kerana ia mempunyai kedalaman yang sama dengan 0 + (x + 1)(x + 1), dikira sebagai hasil tambah.

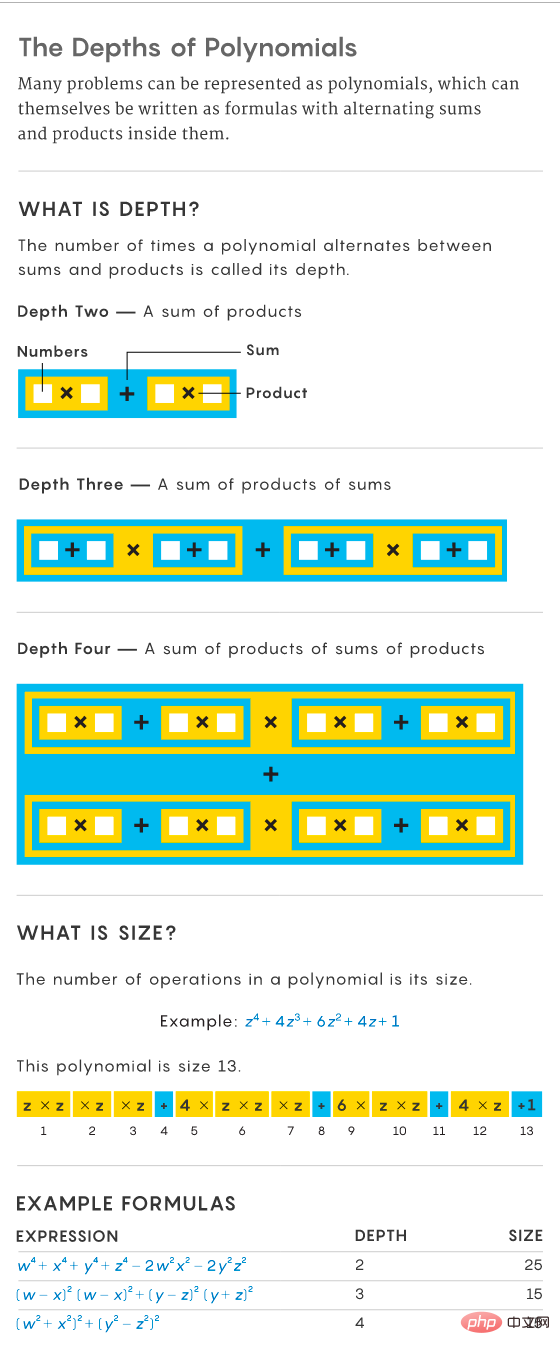
Untuk memudahkan polinomial, saintis komputer mengekangnya kepada bentuk tetap dengan sifat yang dipanggil "kedalaman malar," di mana corak jumlah dan produk tidak berubah dari semasa ke semasa. berubah apabila masalah semakin meningkat. Ini menjadikan saiznya lebih tetap, dengan saiz polinomial berkurangan apabila kedalamannya bertambah. Ungkapan untuk beberapa kedalaman malar dipanggil formula. Kedalaman yang berterusan membolehkan lebih banyak kemajuan dalam kajian polinomial.

Kedalaman" ajaib

Pada tahun 1996, kertas kerja oleh Nisan dan Wigderson memfokuskan pada menyelesaikan masalah pendaraban matriks Mereka memudahkan masalah dalam dua cara. Pertama, mereka menyatakannya menggunakan formula untuk kedalaman malar - kedalaman 3. Kedua, mereka hanya menganggap formula dengan beberapa struktur mudah di mana setiap pembolehubah mempunyai eksponen maksimum 1, yang menjadikan masalah asal sebagai masalah "berbilang linear".

Saintis komputer telah menemui bahawa masalah tertentu boleh ditukar kepada struktur set-multilinear yang agak mudah dengan kos peningkatan sub-eksponen dalam saiz polinomial (setanding dengan kadar pertumbuhan pertumbuhan eksponen).

Nisan dan Wigderson kemudiannya menunjukkan bahawa masalah pendaraban matriks mengambil masa eksponen untuk diselesaikan apabila matriks berkembang. Dalam erti kata lain, mereka menunjukkan bahawa masalah penting adalah sukar, dan mereka berusaha untuk menunjukkan bahawa kelas masalah itu sukar. Walau bagaimanapun, keputusan mereka hanya berlaku untuk formulasi dengan struktur berbilang linear kolektif yang ringkas.

Leslie Valiant

Meningkatkan kedalaman polinomial selalunya akan menyebabkan saiznya mengecil. Dari masa ke masa, saintis komputer telah membuat pertukaran antara kedua-dua sifat ini lebih tepat. Mereka menunjukkan bahawa menambah dua tahap kedalaman kepada kedalaman 3, polinomial berbilang linear ensembel boleh mengimbangi penambahan saiz struktur berbilang linear ensembel mereka. Jika formula berstruktur pada kedalaman 5 mengambil masa eksponen, begitu juga dengan formula kedalaman 3 yang bersifat umum dan tidak berstruktur.

Karya baharu oleh Srikanth Srinivasan et al menunjukkan bahawa rumusan berbilang linear 5 set dalam masalah pendaraban matriks memang berkembang pada kadar eksponen. Ini bermakna formula kedalaman am 3 juga mengambil masa eksponen. Mereka kemudian menunjukkan bahawa corak yang sama berlaku untuk semua kedalaman (bukan hanya 3 dan 5). Dengan hubungan ini, mereka menunjukkan bahawa saiz formula umum bagi sebarang kedalaman untuk masalah yang sama berkembang secara eksponen dengan saiz masalah.

Mereka juga menunjukkan bahawa sukar untuk menyatakan pendaraban matriks dalam formula dengan kedalaman malar, tidak kira apa kedalaman itu.

Hasil kajian ini memberikan pemahaman umum pertama apabila masalah aritmetik adalah "keras" - apabila ia tidak dapat dinyatakan dalam formula kedalaman malar. Masalah khusus pendaraban matriks dikenali sebagai masalah VP. Dan diketahui bahawa masalah VP agak mudah apabila ia tidak terhad kepada kedalaman yang berterusan, jadi ternyata kedalaman yang berterusan adalah punca "kesukaran" masalah.

Adakah masalah VNP lebih sukar daripada masalah VP? Keputusan baharu tidak menunjukkan ini secara langsung, ia hanya menunjukkan bahawa formula kedalaman malar adalah sukar. Tetapi ini masih merupakan peristiwa penting dalam membuktikan bahawa masalah VNP tidak boleh setara dengan masalah VP.

Untuk masalah P vs. NP yang lebih besar, kita kini boleh lebih optimis bahawa jawapannya suatu hari nanti akan ditemui. Lagipun, untuk menyelesaikan masalah yang sukar, kita perlu mengetahui arah mana yang tidak ada harapan.

Atas ialah kandungan terperinci Bagaimana untuk membuktikan bahawa masalah adalah masalah VPN? Para saintis komputer telah menemui cara yang mudah. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!