AI boleh membuktikan 82% masalah dalam pangkalan data matematik SOTA baharu telah dicapai, dan ia masih berdasarkan Transformer.

Saya perlu katakan bahawa saintis taksub memberikan pelajaran matematik AI baru-baru ini.

Tidak, pasukan Facebook juga telah menyertai keseronokan dan mencadangkan model baharu yang boleh mengautomasikan sepenuhnya demonstrasi teorem dan jauh lebih baik daripada SOTA.

Anda mesti tahu bahawa apabila teorem matematik menjadi lebih kompleks, ia hanya akan menjadi lebih sukar untuk membuktikan teorem semata-mata melalui usaha manusia.

Oleh itu, menggunakan komputer untuk menunjukkan teorem matematik telah menjadi tumpuan penyelidikan.

OpenAI sebelum ini telah mencadangkan model GPT-f yang mengkhusus dalam arah ini, yang boleh menunjukkan 56% masalah dalam Metamath.

Kaedah terbaru yang dicadangkan kali ini boleh meningkatkan jumlah ini kepada 82.6%.

Pada masa yang sama, penyelidik mengatakan bahawa kaedah ini mengambil sedikit masa dan boleh mengurangkan penggunaan pengkomputeran kepada satu persepuluh daripada yang asal berbanding dengan GPT-f.

Bolehkah dikatakan kali ini AI akan berjaya dalam pertempurannya dengan matematik

Atau Transformer

Kaedah yang dicadangkan dalam artikel ini ialah program latihan dalam talian berdasarkan Transformer? .

boleh dibahagikan secara kasar kepada tiga langkah:

Pertama , pra-latihan dalam perpustakaan bukti matematik; , memperhalusi model dasar pada set data yang diselia;

Ketiga, , latih model dasar dan model pertimbangan dalam talian.

Secara khusus, ia menggunakan algoritma carian untuk membolehkan model belajar daripada perpustakaan bukti matematik sedia ada, dan kemudian mempromosikannya untuk membuktikan lebih banyak masalah. Perpustakaan bukti matematik merangkumi tiga jenis, iaitu Metamath, Lean dan persekitaran bukti yang dibangunkan sendiri.

Ringkasnya, perpustakaan bukti ini menukar bahasa matematik biasa kepada bentuk yang serupa dengan bahasa pengaturcaraan.

Pustaka utama Metamath ialah set.mm, yang mengandungi kira-kira 38,000 bukti berdasarkan teori set ZFC.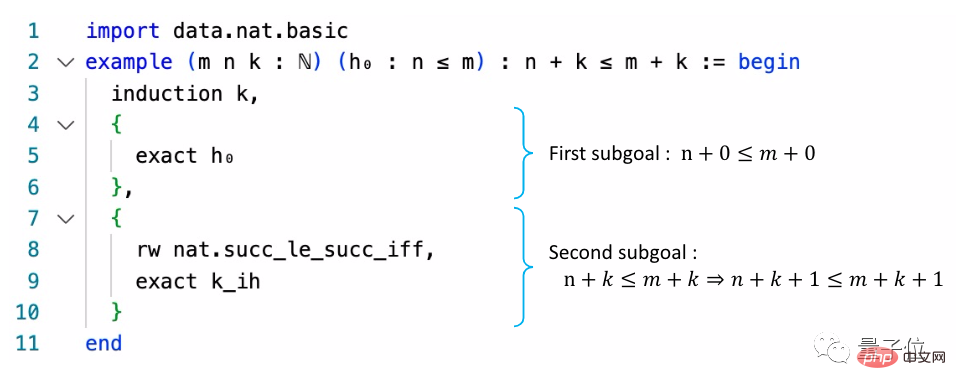

Lean lebih dikenali sebagai algoritma AI Microsoft yang boleh menyertai pertandingan IMO. Perpustakaan Lean direka untuk mengajar algoritma dengan nama yang sama semua pengetahuan matematik sarjana muda dan membiarkannya belajar untuk membuktikan teorem ini.

Matlamat utama penyelidikan ini adalah untuk membina prover yang secara automatik boleh menjana satu siri strategi yang sesuai untuk membuktikan masalah.

Untuk tujuan ini, penyelidik mencadangkan algoritma carian kalis hipergraf bukan keseimbangan berdasarkan MCTS.

MCTS diterjemahkan sebagai Carian Pokok Monte Carlo, yang sering digunakan untuk menyelesaikan masalah pokok permainan Ia terkenal kerana AlphaGo.

Proses pengendaliannya adalah untuk mencari tindakan yang menjanjikan dengan mengambil sampel secara rawak dalam ruang carian, dan kemudian mengembangkan pepohon carian berdasarkan tindakan ini.

Idea yang diterima pakai dalam kajian ini adalah serupa dengan ini.

Proses kalis carian bermula dari matlamat g, mencari kaedah ke bawah dan secara beransur-ansur berkembang menjadi hipergraf.

Apabila set kosong muncul di bawah cawangan, ini bermakna bukti optimum telah ditemui.

Akhir sekali, semasa proses perambatan belakang, rekodkan nilai nod dan jumlah bilangan operasi supertree.

Dalam pautan ini, penyelidik menganggap model strategi dan model pertimbangan.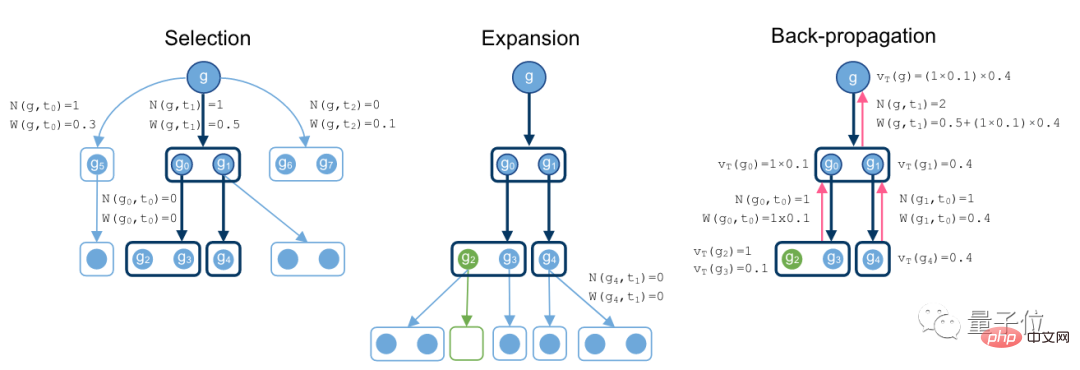

Model dasar membenarkan pensampelan oleh model pertimbangan yang menilai keupayaan strategi semasa untuk mencari bukti.

Seluruh algoritma carian menggunakan dua model di atas sebagai rujukan.

Kedua-dua model ini ialah model Transformer dan berkongsi berat.

Seterusnya, datang peringkat latihan dalam talian.

Dalam proses ini, pengawal akan menghantar penyata kepada pengesahan HTTPS tak segerak dan mengumpul data latihan dan bukti.

Pengesah kemudian akan menghantar sampel latihan kepada jurulatih yang diedarkan dan menyegerakkan salinan modelnya secara berkala.

Hasil eksperimen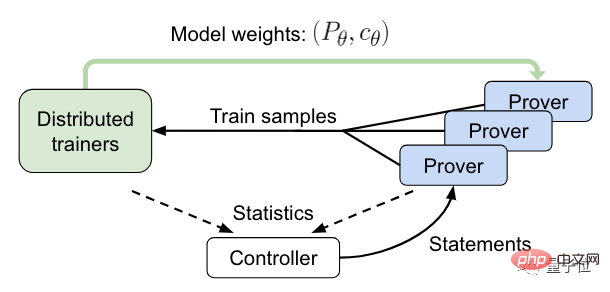

Dalam sesi ujian, penyelidik membandingkan HTPS dengan GPT-f.

Yang terakhir ialah model penaakulan teorem matematik yang sebelum ini dicadangkan oleh OpenAI, juga berdasarkan Transformer.

Keputusan menunjukkan bahawa model selepas latihan dalam talian boleh membuktikan 82% masalah dalam Metamath, jauh melebihi rekod sebelumnya iaitu 56.5% GPT-f.

Dalam perpustakaan Lean, model ini boleh membuktikan 43% teorem, iaitu 38% lebih tinggi daripada SOTA Berikut ialah soalan ujian IMO yang dibuktikan oleh model ini.

Tetapi ia masih belum sempurna.

Sebagai contoh, dalam soalan berikut, ia tidak menyelesaikan soalan dengan cara yang paling mudah. ​​Para penyelidik berkata ini adalah kerana kesilapan dalam anotasi.

Satu Perkara Lagi

Menggunakan komputer untuk menunjukkan masalah matematik, bukti teorem empat warna adalah salah satu contoh yang paling terkenal.

Teorem empat warna adalah salah satu daripada tiga masalah utama dalam matematik moden Ia menyatakan bahawa "mana-mana peta boleh menggunakan hanya empat warna untuk mewarnakan negara dengan sempadan biasa dalam warna yang berbeza."

Memandangkan demonstrasi teorem ini memerlukan banyak pengiraan, tiada siapa yang dapat menunjukkannya sepenuhnya dalam tempoh 100 tahun selepas ia dicadangkan.

Sehingga 1976, selepas 1,200 jam dan 10 bilion penghakiman pada dua komputer di Universiti Illinois, akhirnya dapat menunjukkan bahawa mana-mana peta hanya memerlukan 4 warna untuk menandakannya. Ia mengejutkan seluruh komuniti matematik.

Selain itu, apabila masalah matematik menjadi lebih kompleks, ia menjadi lebih sukar untuk menggunakan kuasa manusia untuk memeriksa sama ada teorem itu betul.

Baru-baru ini, komuniti AI telah memberi tumpuan secara beransur-ansur kepada masalah matematik.

Pada tahun 2020, OpenAI melancarkan model penaakulan teorem matematik GPT-f, yang boleh digunakan untuk pembuktian teorem automatik.

Kaedah ini boleh melengkapkan 56.5% daripada bukti dalam set ujian, melebihi model SOTA MetaGen-IL pada masa itu sebanyak lebih daripada 30%.

Pada tahun yang sama, Microsoft juga mengeluarkan Lean, yang boleh membuat soalan ujian IMO, yang bermaksud bahawa AI boleh membuat soalan yang tidak pernah dilihat sebelum ini.

Tahun lepas, selepas OpenAI menambah pengesah pada GPT-3, prestasi masalah matematik adalah jauh lebih baik daripada kaedah penalaan halus sebelumnya, dan ia boleh mencapai 90% daripada tahap pelajar sekolah rendah.

Pada Januari tahun ini, kajian bersama dari MIT + Harvard + Columbia University + University of Waterloo menunjukkan bahawa model yang mereka cadangkan boleh melakukan matematik tinggi.

Ringkasnya, saintis bekerja keras untuk menjadikan AI, subjek separa, menjadi seni liberal dan sains.

Atas ialah kandungan terperinci AI boleh membuktikan 82% masalah dalam pangkalan data matematik SOTA baharu telah dicapai, dan ia masih berdasarkan Transformer.. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!