Kandungan objek ndarray boleh diakses dan diubah suai melalui pengindeksan atau penghirisan, sama seperti operasi penghirisan untuk senarai dalam Python.
Tatasusunan ndarray boleh diindeks berdasarkan subskrip dari 0 ~ n-1 Objek hirisan boleh diperolehi daripada tatasusunan asal melalui fungsi hirisan terbina dalam dan menetapkan permulaan , parameter henti dan langkah Potong tatasusunan baharu.
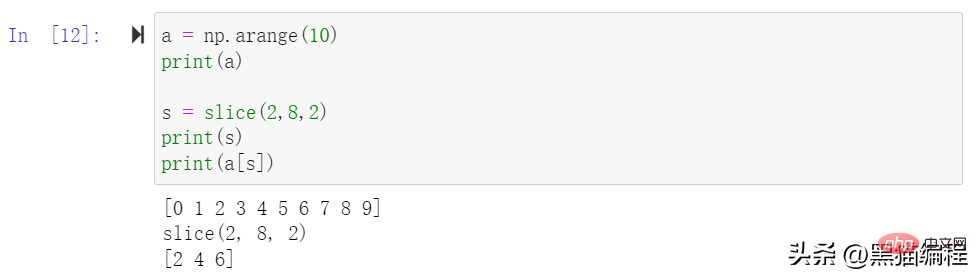
Kepingan juga boleh termasuk elips... , datang Jadikan panjang tuple pemilihan sama dengan dimensi tatasusunan. Jika elipsis digunakan pada kedudukan baris, ia akan mengembalikan ndarray yang mengandungi elemen dalam baris.
Contoh berikut mendapat tatasusunan (0,0), (1,1) dan (2,0).
a = np.array([[0,1,2], [3,4,5], [6,7,8], [9,10,11]])
print(a)
print('-' * 20)
rows = np.array([[0,0], [3,3]])
cols = np.array([[0,2], [0,2]])
b = a[rows, cols]
print(b)
print('-' * 20)
rows = np.array([[0,1], [2,3]])
cols = np.array([[0,2], [0,2]])
c = a[rows, cols]
print(c)
print('-' * 20)
rows = np.array([[0,1,2], [1,2,3], [1,2,3]])
cols = np.array([[0,1,2], [0,1,2], [0,1,2]])
d = a[rows, cols]
print(d)[[ 012] [ 345] [ 678] [ 9 10 11]] -------------------- [[ 02] [ 9 11]] -------------------- [[ 05] [ 6 11]] -------------------- [[ 048] [ 37 11] [ 37 11]]
Hasil yang dikembalikan ialah ndarray yang mengandungi setiap objek elemen sudut .
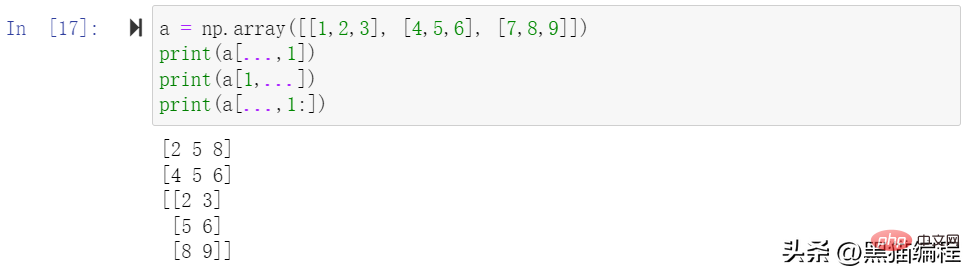
boleh digabungkan dengan tatasusunan diindeks menggunakan kepingan: atau …. Contohnya:
a = np.array([[1,2,3], [4,5,6], [7,8,9]])
print(a)
print('-' * 20)
b = a[1:3, 1:3]
print(b)
print('-' * 20)
c = a[1:3, [0,2]]
print(c)
print('-' * 20)
d = a[..., 1:]
print(d)[[1 2 3] [4 5 6] [7 8 9]] -------------------- [[5 6] [8 9]] -------------------- [[4 6] [7 9]] -------------------- [[2 3] [5 6] [8 9]]
Kita boleh mengindeks tatasusunan sasaran melalui tatasusunan Boolean.
Indeks Boolean menggunakan operasi Boolean (seperti operator perbandingan) untuk mendapatkan tatasusunan elemen yang memenuhi syarat yang ditetapkan.
Contoh berikut memperoleh elemen lebih besar daripada 5:
a = np.array([[1,2,3], [4,5,6], [7,8,9]])
print(a)
print('-' * 20)
print(a[a > 5])[[1 2 3] [4 5 6] [7 8 9]] -------------------- [6 7 8 9]
Contoh berikut menggunakan ~ ( operator pelengkap) untuk menapis NaN.
a = np.array([np.nan, 1, 2, np.nan, 3, 4, 5])
print(a)
print('-' * 20)
print(a[~np.isnan(a)])[nan1.2. nan3.4.5.] -------------------- [1. 2. 3. 4. 5.]
Contoh berikut menunjukkan cara menapis unsur bukan majmuk daripada tatasusunan.
a = np.array([1, 3+4j, 5, 6+7j])
print(a)
print('-' * 20)
print(a[np.iscomplex(a)])[1.+0.j 3.+4.j 5.+0.j 6.+7.j] -------------------- [3.+4.j 6.+7.j]
Pengindeksan mewah merujuk kepada menggunakan tatasusunan integer untuk pengindeksan.
Indeks mewah mengambil nilai berdasarkan nilai tatasusunan indeks sebagai subskrip paksi tatasusunan sasaran.Untuk menggunakan tatasusunan integer satu dimensi sebagai indeks, jika sasaran ialah tatasusunan satu dimensi, maka hasil indeks ialah elemen pada kedudukan yang sepadan Jika sasaran ialah dua-. tatasusunan dimensi, maka ia adalah baris yang sepadan dengan subskrip.
Pengindeksan mewah berbeza daripada penghirisan, ia sentiasa menyalin data ke dalam tatasusunan baharu.
Susun atur satu dimensi
a = np.arange(2, 10)
print(a)
print('-' * 20)
b = a[[0,6]]
print(b)[2 3 4 5 6 7 8 9] -------------------- [2 8]
Susun atur dua dimensi
1. Lulus dalam tatasusunan indeks urutan
a = np.arange(32).reshape(8, 4)
print(a)
print('-' * 20)
print(a[[4, 2, 1, 7]])[[ 0123] [ 4567] [ 89 10 11] [12 13 14 15] [16 17 18 19] [20 21 22 23] [24 25 26 27] [28 29 30 31]] -------------------- [[16 17 18 19] [ 89 10 11] [ 4567] [28 29 30 31]]
2
a = np.arange(32).reshape(8, 4) print(a[[-4, -2, -1, -7]])
[[16 17 18 19] [24 25 26 27] [28 29 30 31] [ 4567]]
np.ix_ fungsi adalah untuk memasukkan dua tatasusunan, menghasilkan hubungan pemetaan produk Cartesian.
Hasil Cartesian merujuk kepada hasil Cartesan (hasil Cartesian) daripada dua set X dan Y dalam matematik, juga dikenali sebagai hasil langsung, dinyatakan sebagai
X×Y, objek pertama ialah ahli X dan objek kedua ialah salah satu daripada semua pasangan tertib Y yang mungkin. Contohnya, A={a,b}, B={0,1,2}, kemudian:
A×B={(a, 0), (a, 1), (a, 2), (b, 0), (b, 1), (b, 2)}
B×A={(0, a), (0, b), (1, a), (1, b), (2, a), (2, b)}a = np.arange(32).reshape(8, 4) print(a[np.ix_([1,5,7,2], [0,3,1,2])])
[[ 4756] [20 23 21 22] [28 31 29 30] [ 8 119 10]]
如果两个数组 a 和 b 形状相同，即满足 a.shape == b.shape，那么 a*b 的结果就是 a 与 b 数组对应位相乘。这要求维数相同，且各维度的长度相同。a = np.arange(1, 5)
b = np.arange(1, 5)
c = a * b
print(c)
[ 149 16]
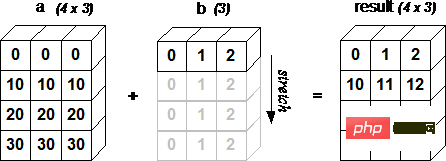
当运算中的 2 个数组的形状不同时，numpy 将自动触发广播机制。如：
a = np.array([ [0, 0, 0], [10, 10, 10], [20, 20, 20], [30, 30, 30] ]) b = np.array([0, 1, 2]) print(a + b)
[[ 012] [10 11 12] [20 21 22] [30 31 32]]
下面的图片展示了数组 b 如何通过广播来与数组 a 兼容。
tile扩展数组
a = np.array([1, 2])
b = np.tile(a, (6, 1))
print(b)
print('-' * 20)
c = np.tile(a, (2, 3))
print(c)[[1 2] [1 2] [1 2] [1 2] [1 2] [1 2]] -------------------- [[1 2 1 2 1 2] [1 2 1 2 1 2]]
4x3 的二维数组与长为 3 的一维数组相加，等效于把数组 b 在二维上重复 4 次再运算：
a = np.array([ [0, 0, 0], [10, 10, 10], [20, 20, 20], [30, 30, 30] ]) b = np.array([0, 1, 2]) bb = np.tile(b, (4, 1)) print(a + bb)
[[ 012] [10 11 12] [20 21 22] [30 31 32]]
广播的规则:
简单理解：对两个数组，分别比较他们的每一个维度（若其中一个数组没有当前维度则忽略），满足：
若条件不满足，抛出 "ValueError: frames are not aligned" 异常。
Atas ialah kandungan terperinci Penjelasan terperinci tentang modul analisis data Python Penghirisan, pengindeksan dan penyiaran Numpy. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
![[Web front-end] Permulaan pantas Node.js](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
